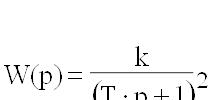Моделирование на микро- и макроуровне. Построение математической модели колебания круглой мембраны. Исследование гидравлической системы, страница 2

,

где      Т - период, с;

k - коэффициента передачи.

   

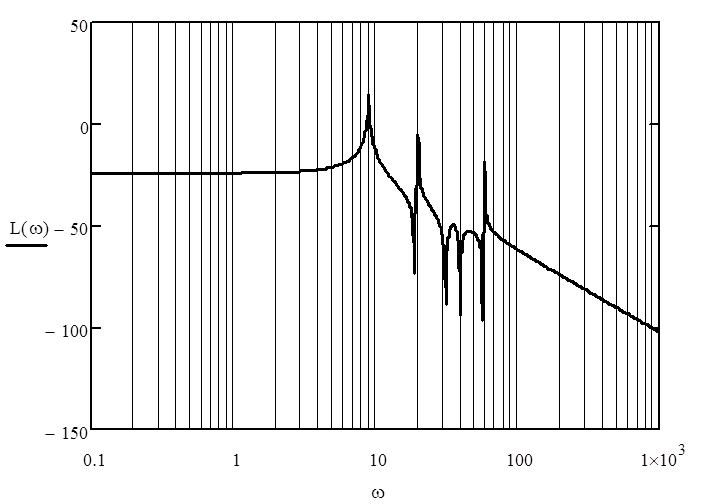
Рисунок 6 – График логарифмической амплитудно-частотной характеристики.

Найдем Т при условии, что:

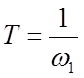
где      ω₁ - частота аппроксимированной ЛАЧХ, Гц.

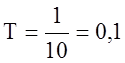 [с]

График ЛАЧХ пересекает ось Y в точке -24. Определим значение коэффициента передачи k:

20∙lgk = -24, ,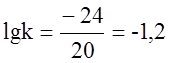

С помощью аппроксимации передаточная функция запишется в виде:

.

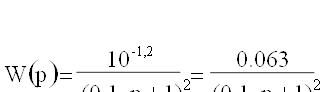2 МОДЕЛИРОВАНИЕ НА МАКРОУРОВНЕ

2.1 Графические формы математической модели гидравлической системы

На Рисунке 1 приведена расчетная схема гидравлической системы, состоящей из потребителей выходного расхода с устройства 1,2; насоса потока управления 3 с клапаном 4, использование которого позволяет рассматривать насос как источник постоянного давления; насоса потока питания 5 с клапаном 6 и соединяющих магистралей.

 

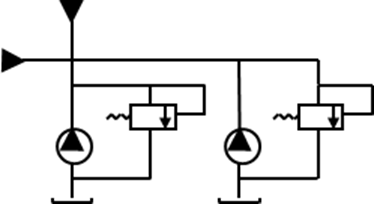
Рисунок 1 - Схема гидравлической системы

При построении модели учтены основные свойства гидравлической системы. Гидравлические магистрали представлены как дискретные элементы, наделенные инерционными и диссипативными свойствами, а масса жидкости в них – как сосредоточенная. Электрогидравлический вихревой элемент также рассмотрен как элемент, обладающий инерционными и диссипативными свойствами. В точках ветвления установлены упругие элементы, учитывающие сжимаемость жидкости и деформируемость трубопровода. Внешние воздействия на систему представлены в виде источников потенциалов – давлений насосов и потребителей. На рисунке 2 представлена динамическая модель гидравлической системы.

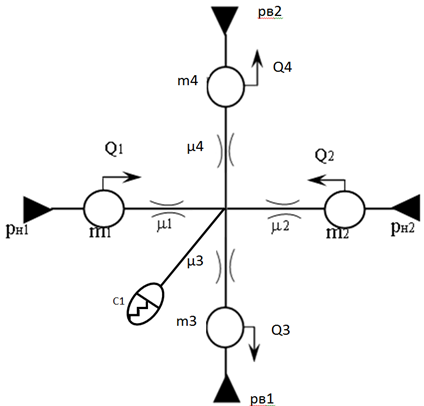
Рисунок 2 - Динамическая модель гидравлической системы

На основании динамической модели построен ориентированный граф, являющийся графической формой модели гидравлической системы и позволяющий идентифицировать структуру и физические свойства системы (Рисунок 3). 

Ветви упругих элементов расставлены от насосов к электрогидравлическому элементу  и от него к потребителям.

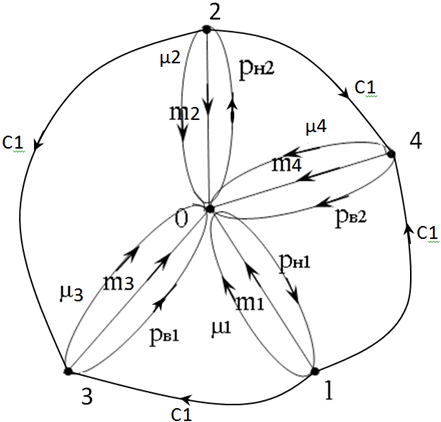
Рисунок 3 - Ориентированный граф гидравлической системы

Таким образом, исходная схема гидравлической системы (Рисунок 1) представлена в двух графических формах: динамической модели (Рисунок 2) и ориентированного графа (Рисунок 3).

2.2 Расчет параметров гидравлической системы

Для исходных данных, представленных в таблице 1 и 2 проведём расчет параметров гидравлической системы. Результаты расчета представлены в таблице 3.

Таблица 1 – Исходные данные

Обозначение	Основные параметры	Значение
	Плотность рабочей жидкости	860 кг/м3
	Вязкость	0,15·10-4 м2/с
ЕС	Модуль упругости газожидкостной смеси	1,7·108 Па
Етр	Модуль упругости трубопровода	2,1·1011 Па
	Коэффициент потерь на трение при турбулентном потоке	0,03
	Толщина стенки трубопровода	2∙10-3 м

Таблица 2 – Параметры трубопроводов

Параметр	Номер трубопровода
	1	2	3	4
Диаметр трубопровода dтр, м	0,025	0,03	0,03	0,032
Длина трубопровода l, м	1,5	2,5	2	0,9
Коэффициент местных сопротивлений ξ	4	5,5	5	3
Давление потребителей и насосов P, ∙106 Па	0,2	0,25	0,3	0.25, 0.5

Таблица 3 – Результаты расчета

Параметры	Формула	Магистраль
		1	2	3	4
1. Площадь сечения магистрали	.	0.00049	0.0007	0.0007	0,0008
2. Объём участка трубопровода	.	0.00074	0.0018	0.0014	0,00072
3. Доля объёма	.	0.188	0.451	0.361	0,185
4. Коэффициент массы	.	2628000	3042000	2433000	962400
5. Коэффициент линейных	.	2024000	1627000	1301000	453300
6. Коэффициент нелинейных		1035∙107	6884∙106	6024∙106	2555∙106
7. Коэффициент жесткости участка		1035∙109	2107∙108	3292∙108	1255∙109

Общий коэффициент жесткости при разветвлении трубопровода:

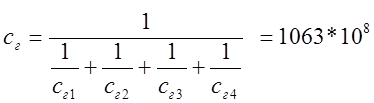
2.3 Узловой метод формирования математической модели гидравлической системы

На основании орграфа (Рисунок 1) сформируем матрицу инциденций (таблица 4), по правилам, изложенным в основных теоретических сведениях.

Таблица 4 - Матрица инциденций гидравлической системы

Узлы	Ветви
	Источники потенциалов				Упругие	Диссипативные				Инерционные
	рН1	рН2	рВ1	рВ2	с1	μ1	μ2	μ3	μ4	m1	m2	m3	m4
1	1	0	0	0	-1	-1	0	0	0	-1	0	0	0
2	0	1	0	0	-1	0	-1	0	0	0	-1	0	0
3	0	0	-1	0	1	0	0	-1	0	0	0	-1	0
4	0	0	0	-1	1	0	0	0	-1	0	0	0	-1
	АВ				АУ	АД				АИ

На основании матрицы инциденций запишем подматрицы упругих А_У,  диссипативных А_Д , инерционных А_И элементов и подматрицу источников потенциалов А_В:

,      ,      ,

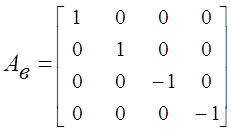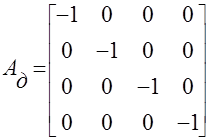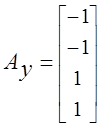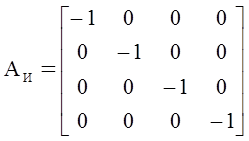
Матрицы параметров инерционных, упругих и диссипативных элементов гидравлической системы соответственно:

,   ,    .

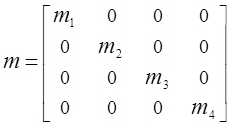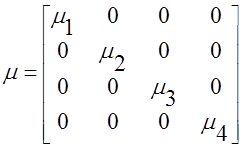Матрица потенциалов источников Р_в, упругих  Р_у и диссипативных Р_д, элементов и матрица фазовых переменных типа потока Q: