Методы оценки точности регулирования линейных систем

Методы оценки точности регулирования линейных систем.

Автоматическая система должна обеспечивать требуемые показатели качества регулирования.

Качество процесса регулирования система системы, как правило, оценивается по ее переходной характеристике. Основными показателями качества являются время регулирования, перерегулирование, колебательность и установившаяся ошибка. Кроме того, следует отметить, что в конкретных условиях к качеству регулирования могут предъявляться и другие требования, например, максимальная скорость изменения регулируемой величины, основная частота ее колебаний и т. п.

Временем регулирования t_р называют время, в течении которого начиная с момента приложения воздействия на систему отклонения регулируемой величины от ее установившегося значения меньше априорно заданного значения (обычно 5%). Таким образом, время регулирования определяет длительность (быстродействие) переходного процесса.

Перерегулированием называют максимальное отклонениерегулируемой величины от установившегося значения, выраженное в процентах. Данный критерий характеризует точность и плавность переходного процесса.

Колебательность системы характеризуется числом колебаний регулируемой величины за время регулирования. Если за это время переходной процесс в системе совершает число колебаний меньше заданного, то считается, что система имеет требуемое качество регулирования по колебательности.

Установившееся значение регулируемой величины по окончании переходного процесса при изменении входного воздействия может быть представлен в виде суммы двух составляющих:

где y(t) – решение дифференциального уравнения, описывающего систему; y_св(t) – общее решение однородного дифференциального уравнения (свободная составляющая); y_вын(t) – частное решение неоднородного дифференциального уравнения (вынужденная составляющая), характеризующее поведение системы в установившемся режиме и определяемое входным воздействием.

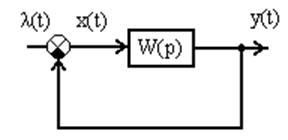
Рис. 24. Типичная структурная схема исследуемых систем.

Для всех систем, имеющих типичную структурную схему (см. Рис. 24.) свободную составляющую решения можно представить в виде:

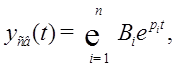
где B_i – постоянные коэффициенты, определяющиеся параметрами системы и начальными условиями, а p_i – корни характеристического уравнения системы.

Свободная составляющая определяет показатели качества переходного процесса, а показатели точности системы описываются вынужденной составляющей.

Рассмотрим показатели качества, характеризующиеся вынужденной составляющей отклика системы.

Значение ошибки в установившемся режиме:

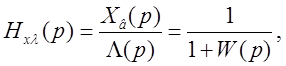
Разложим H_xλ в ряд по степеням p в окрестности точки p = 0, что соответствует установившемуся режиму системы.

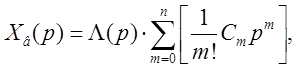 где

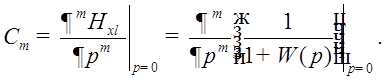
Величины C_m носят название коэффициента ошибок по значению входного воздействия (С₀) или по его производным. Ошибки слежения зависят как от свойств системы, так и от временного изменения входного воздействия  . Функцию   задают степенным рядом:

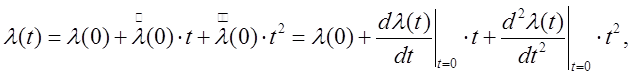
где t = 0 соответствует началу воздействия. В задачах радиоавтоматики сложность  такова, что третьей производной допустимо пренебрегать (ускорение изменяется редко и кратковременно). Установившаяся ошибка тогда содержит три слагаемых:

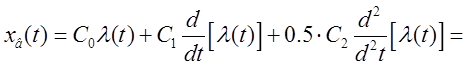
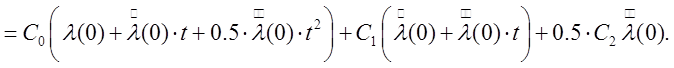
Коэффициент С₀ получил название коэффициента статической ошибки (позиционной ошибки), С₁ – коэффициента скоростной ошибки, а С₂ – коэффициент ошибки по ускорению.

Из данных выражений следует, что ошибка системы в установившемся режиме зависит от входного воздействия.

Если то ошибка системы определяется коэффициентом С₀, выражение для вынужденной ошибки выглядит так:

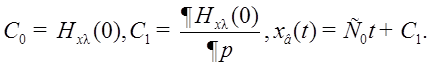Если то  И т. д.

В инженерных расчетах коэффициент ошибок принято определять через коэффициент передачи разомкнутой цепи:

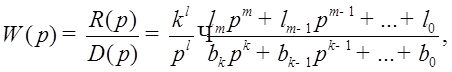
где l – порядок астатизма системы, n = l + k – порядок системы.

        Таблица 3. Значения коэффициентов ошибок для некоторых систем.

Характер системы	Коэффициенты ошибок
	С0	С1, с	С2, с2
Статическая (l = 0)
Астатическая 1-ого порядка (l = 1)	0

Т.о. коэффициент С₀ характеризует добротность системы по положению, С₁ – добротность системы по скорости, а С₂ – добротность системы по ускорению.

Увеличение порядка астатизма приводит к нулевым значениям некоторых коэффициентов ошибок, однако при этом понижается и степень устойчивости системы.

Для статических систем (l = 0)  наибольший вклад в ошибку вносит первое слагаемое и для большинства задач С₁ и С₂ можно пренебречь:

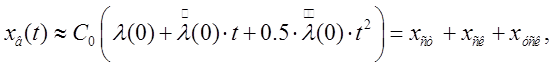
где 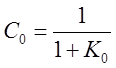 – коэффициент статической ошибки; К₀ – коэффициент передачи (добротность) системы по положению; х_ст – статическая ошибка (статизм системы); х_ск – скоростная ошибка; х_уск – ошибка из-за ускорения:

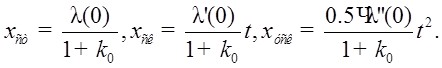
Все составляющие ошибки обратно пропорциональны добротности системы.

Рассмотрим воздействие на статическую систему единичного скачка. При этом  а значит, значение ошибки определяется значением и в установившемся режиме остается постоянным.

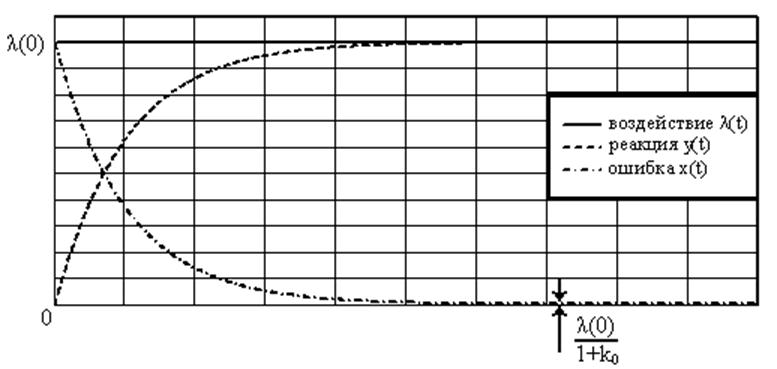
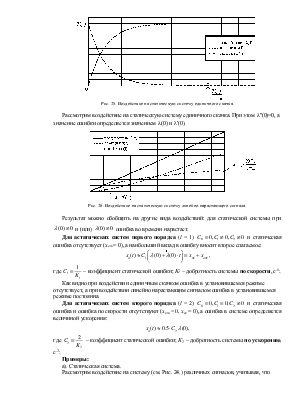
Рис. 25. Воздействие на статическую систему единичного скачка.

Рассмотрим воздействие на статическую систему единичного скачка. При этом а  значение ошибки определяется значением и

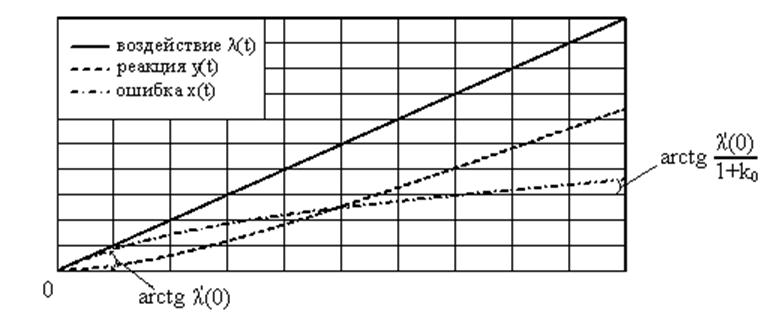
Рис. 26. Воздействие на статическую систему линейно нарастающего сигнала.

Результат можно обобщить на другие вида воздействий: для статической системы при   и (или)  ошибка во времени нарастает.

Для астатических систем первого порядка (l = 1)  и статическая ошибка отсутствует (х_ст = 0), а наибольший вклад в ошибку вносит второе слагаемое:

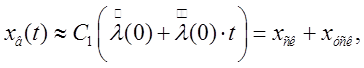
где 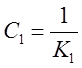 – коэффициент статической ошибки; К₁ – добротность системы по скорости, с^-1;

Как видно при воздействии единичным скачком ошибка в установившемся режиме отсутствует, а при воздействии линейно нарастающим сигналом ошибка в установившемся режиме постоянна.

Для астатических систем второго порядка (l = 2)  и статическая ошибка и ошибка по скорости отсутствуют (х_ст = 0, х_ск = 0), а ошибка в системе определяется величиной ускорения:

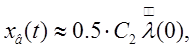
где 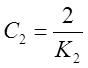 – коэффициент статической ошибки; К₂ – добротность системы по ускорению, с^-2;

Примеры:

а). Статическая система.

Рассмотрим воздействие на систему (см. Рис. 24.) различных сигналов, учитывая, что

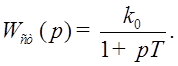
Тогда

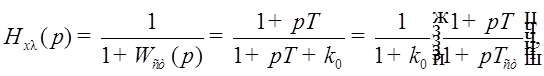 где

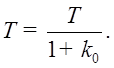
·  Ступенчатое воздействие.

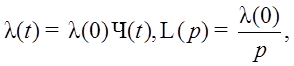
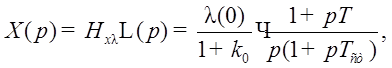
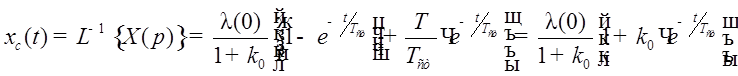
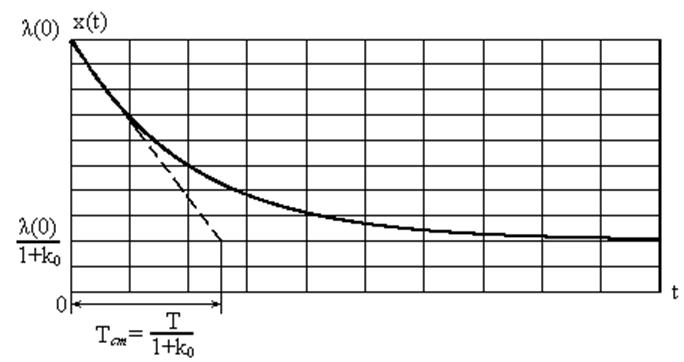
Рис. 27. Ошибка при воздействии на статическую систему единичным скачком.

Найдем значение ошибки в установившемся режиме, пользуясь теоремой об установившемся значении:

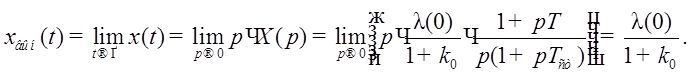
·  Линейное воздействие.

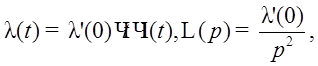
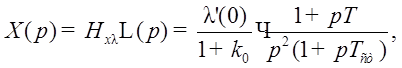
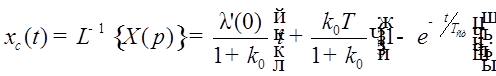
Отклик на линейное воздействие и ошибка показаны на Рис. 26.

Найдем значение ошибки в установившемся режиме, пользуясь понятием коэффициента ошибок:

Найдем значения коэффициентов:

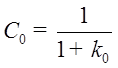
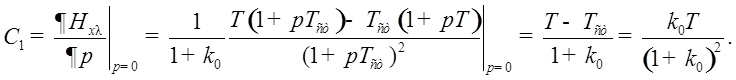
б). Система с астатизмом первого порядка.

Рассмотрим воздействие на систему (см. Рис. 24.) различных сигналов, учитывая, что

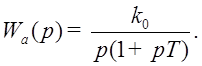
Тогда

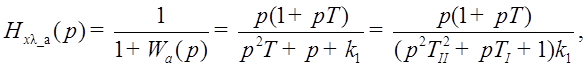 где

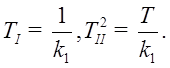
·  Ступенчатое воздействие.

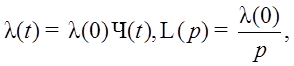
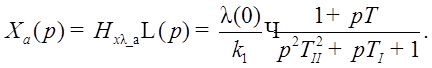
Пусть звено имеет апериодический характер (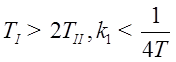), тогда:

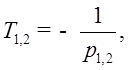 где р_1,2 – корни характеристического уравнения;

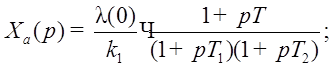
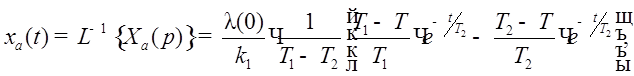
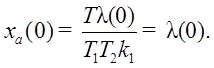
Значения ошибки в установившемся режиме можно получить с помощью коэффициентов ошибок, зная, что С₀=0:

а также, используя теорему об установившемся значении:

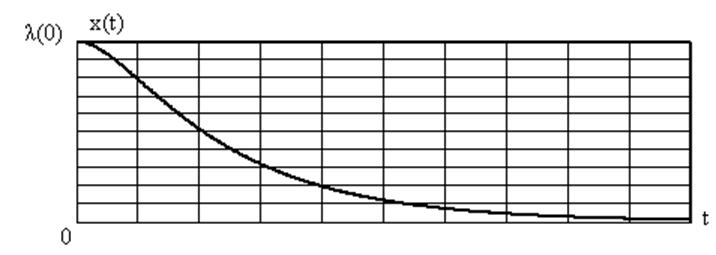
Рис. 28. Ошибка при воздействии на астатическую систему 1- ого порядка единичного скачка.

Найдем значение ошибки в установившемся режиме, пользуясь теоремой об установившемся значении:

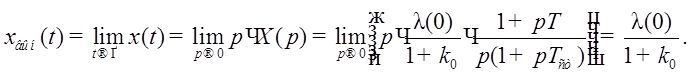
·  Линейное воздействие.

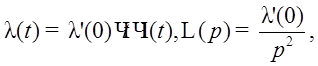
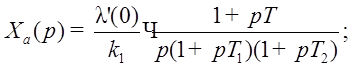
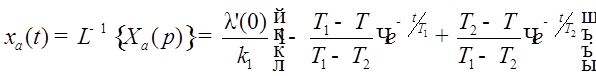
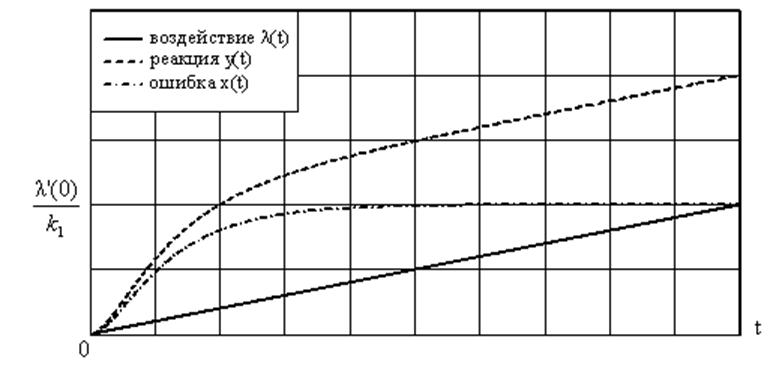
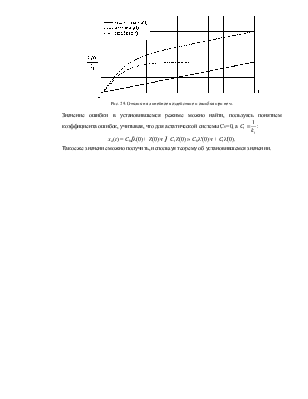
Рис. 29. Отклик на линейное воздействие и ошибка при нем.

Значение ошибки в установившемся режиме можно найти, пользуясь понятием коэффициента ошибок, учитывая, что для астатической системы С₀=0, а :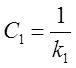

Такое же значение можно получить, используя теорему об установившемся значении.