Классический метод вариационного исчисления

Лекция №8

КЛАССИЧЕСКИЙ МЕТОД ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ

Задачи синтеза алгоритмов оптимального управления объектами в динамике при выбранном функционале критерия качества имеют дополнительные (условные) ограничения в виде уравнений математической модели динамики объекта. Экстремум функционала, определяемый при дополнительных условиях (функциональных ограничениях), называют условным экстремумом. Задачи на условный экстремум при определении оптимальных управлений объектом в динамике обусловлены тем, что функции x_i(t) и u_l(t), входящие в функционал J, не могут варьироваться независимо, так как они связаны уравнением динамики объекта. Траектория выхода у(t) является следствием изменения координаты управления и зависит от вида дифференциального уравнения объекта.

Задача об оптимизации объекта управления в динамике, решаемая классическим вариационным исчислением, имеет следующую формулировку. Задана математическая модель объекта в форме уравнений состояния, представленная при одной координате управления векторным уравнением

.                           (3.64)

Требуется определить оптимальное управлением0 (/), обеспечивающее минимум функционала

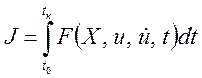,                                (3.65)

в котором X и u связаны уравнениями состояния (3.64), а функция F(...) является непрерывной по всем переменным и имеет непрерывные частные производные первых двух порядков. Функции x_i(t) и u(t) должны быть непрерывными и иметь непрерывные первые производные (i = 1, 2, ..., n). Векторы X₀ и Х_к фиксированы.

Первые задачи на условный экстремум были поставлены и решены основоположниками классического вариационного исчисления Бернулли, Эйлером и Лагранжем. Задачу, определяемую дифференциальными связями типа (3.64) и функционалом (3.65), называют общей задачей Лагранжа. Если функционал характеризует конечное состояние J = G[X(t_к), u(t_к), t_к], то имеем задачу Майера, а если 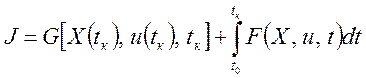 – задачу Больца. Для решения общей задачи Лагранжа используют метод множителей Лагранжа.

При решении задачи на условный экстремум рассматривают вспомогательный функционал

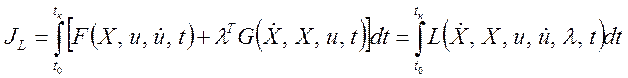,            (3.66)

где l^т = [l₁, l₂,..., l_n] – строка множителей Лагранжа;

.            (3.67)

Функцию  называют функцией Лагранжа, а функцию  – функцией связей, которая определяется исходными уравнениями (3.64):

,                            (3.68)

или

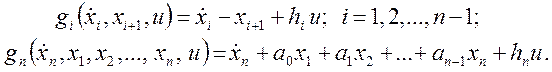
Задачу на безусловный экстремум решают для вспомогательного функционала (3.66). Уравнения Эйлера при этом составляют для функции Лагранжа (i = 1, 2, ..., n):

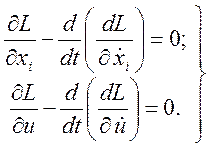                               (3.69)

Эти уравнения называют уравнениями Эйлера – Лагранжа; они характеризуют условие стационарности функционала (3.66). В результате решения уравнений (3.69) с учетом уравнений (3.64) получим оптимальное управление u⁰(t) объектом в динамике.

Уравнения (3.64) и (3.69) являются уравнениями вариационной задачи, порядок которых после исключения координаты управления равен 2n. При решении этих уравнений относительно векторов X и l для заданных X(t₀) и X(t_к) рассматривается двухточечная краевая задача. Сложность решения ее обусловлена тем, что начальные значения множителей Лагранжа l_i(t₀) неизвестны. Чтобы удовлетворить заданным значениям векторов состояния X(t₀) и X(t_к), приходится многократно решать уравнения вариационной задачи, задаваясь различными начальными значениями l_i(t₀).

При определении оптимального управления классическим методом вариационного исчисления уравнения вариационной задачи могут быть записаны в гамильтоновой или канонической форме. Пусть функционал в частном случае зависит от переменных х₁(t) и х₂(t), а также их производных  и :

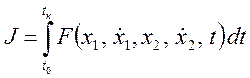.                                   (3.70)

Запишем для него уравнения Эйлера типа (3.60):

                                         (3.71)

От переменных х₁ и х₂ перейдем к новым переменным р₁ и р₂ согласно выражениям

,                                (3.72)

а от функции F – к новой функции

,

В общем случае, при n переменных выражение для функции Н запишем в векторной форме:

,                     (3.73)

где функцию Н называют функцией Гамильтона, а переменные p_i – каноническими переменными.

Дифференцируя (3.73), получаем

.                          (3.74)

На основании уравнений Эйлера и (3.72) запишем

,

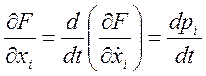При этом вместо (3.74) получим новую систему дифференциальных уравнений, которые называют каноническими уравнениями Гамильтона:

                   (3.75)