Коррекция нелинейных систем. Исследование возможности устранения режимов автоколебаний в нелинейных системах

Лабораторная работа № 5

Коррекция нелинейных систем

Цель работы: исследовать возможность устранения режимов автоколебаний в нелинейных системах.

Общие положения

Для устранения режима автоколебаний или существенного уменьшения их амплитуды в нелинейную систему чаще всего вводят КУ обратной связи, при последовательной коррекции используют нелинейные КУ. Коррекция даже с помощью жесткой обратной связи, охватывающей НЭ, позволяет достичь большего эффекта, чем последовательная коррекция. Поэтому в большинстве САУ вводят ОС по положению регулирующего органа (угла поворота исполнительного механизма) т.к. именно в этом блоке присутствуют нелинейности.

Сложнее всего устранить режим автоколебаний в системе при гистерезисной нелинейности (с зоной неоднозначности). Для этого вводя инерционные гибкие обратные связи, параметры которых либо рассчитывают, либо подбирают при моделировании системы.

Порядок выполнения лабораторной работы

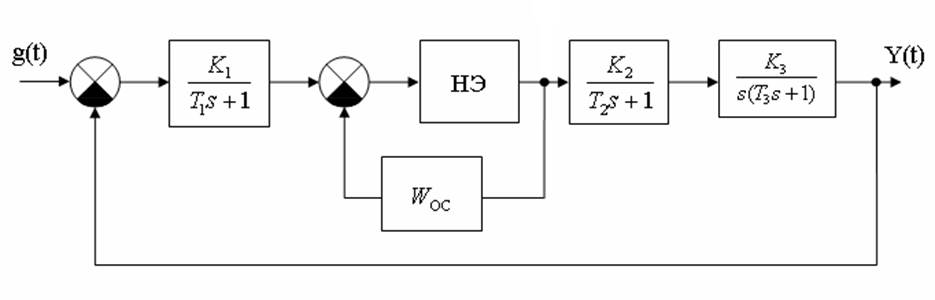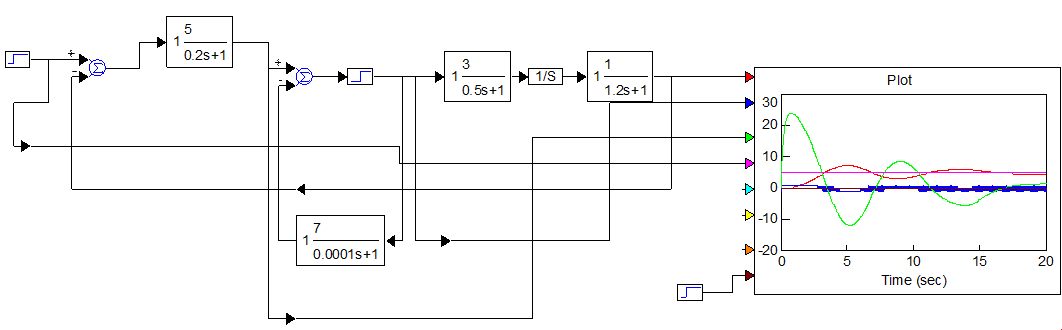
1. Собрать схему в программе VisSim:

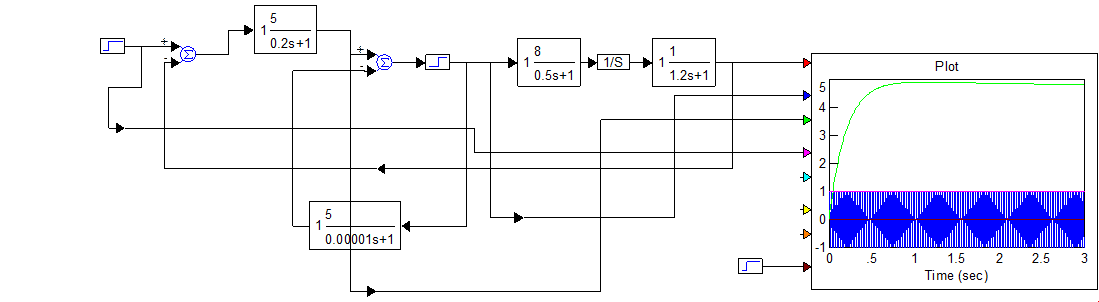
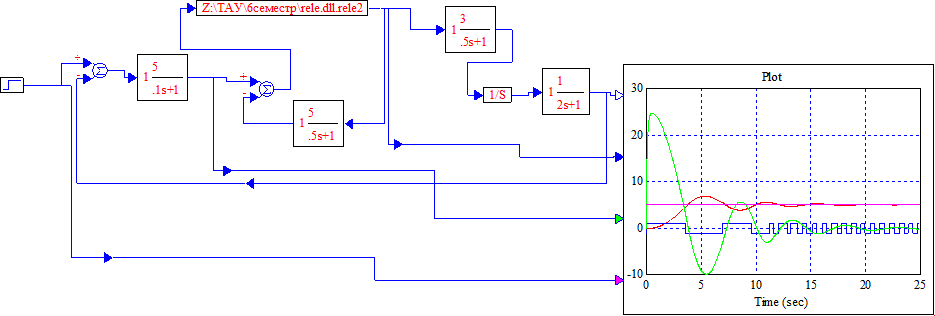
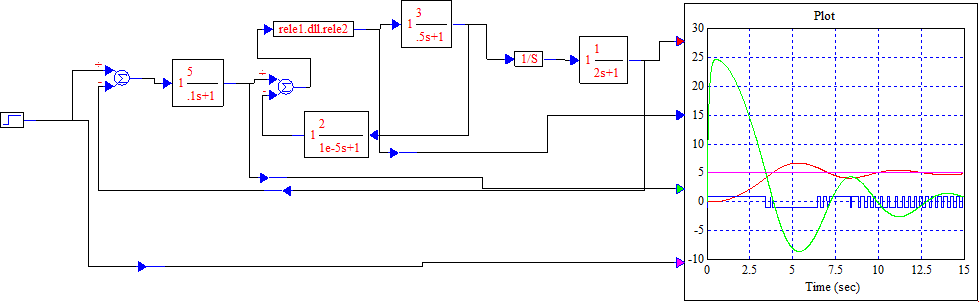
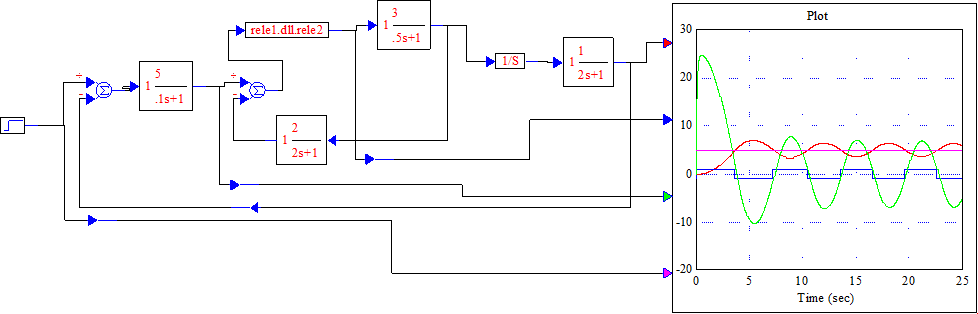
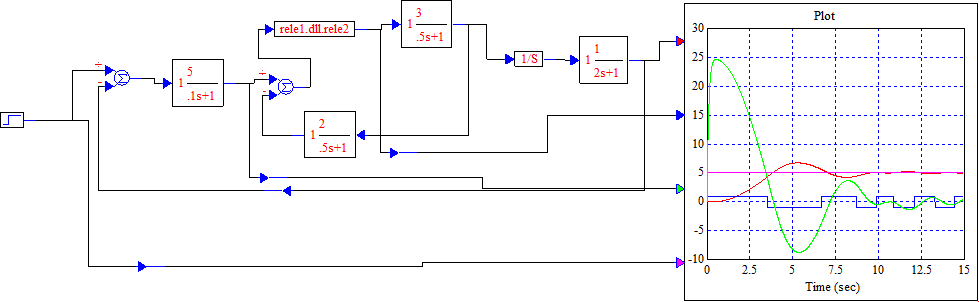
Рисунок 5.1 – Схема моделирования

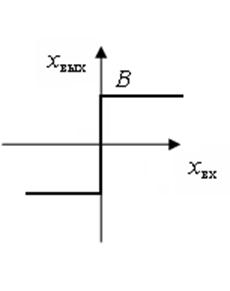
НЭ:

а)                                                 

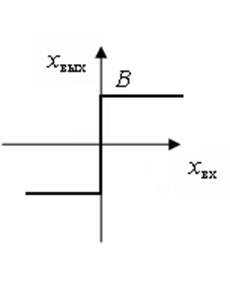
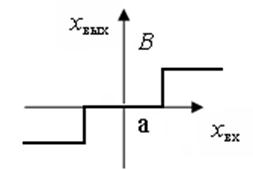
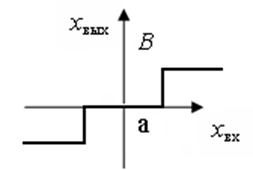
Рисунок 5.2 – Исследуемые нелинейные элементы

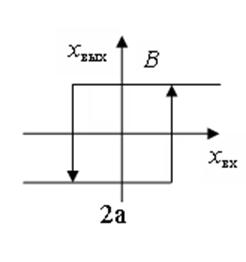
a=2

                                           

                                                     Зона нечувствительности 4

2. Исследовать работу системы без КУ при .

3. Исследовать влияние КУ на поведение системы:

1) W_ос(s)=К_ос;

2) W_ос(s)=К_ос\(T_осS+1).

К_ос=1; Т_ос=Т₂.

4. Исследовать влияние Кос и Тос на режим автоколебаний и его устранение.  Wос(s)=Кос  и  Wос(s)=Кос\(TосS+1).

;

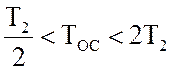
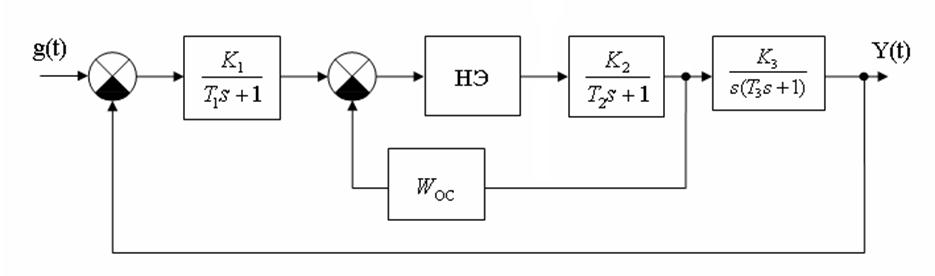
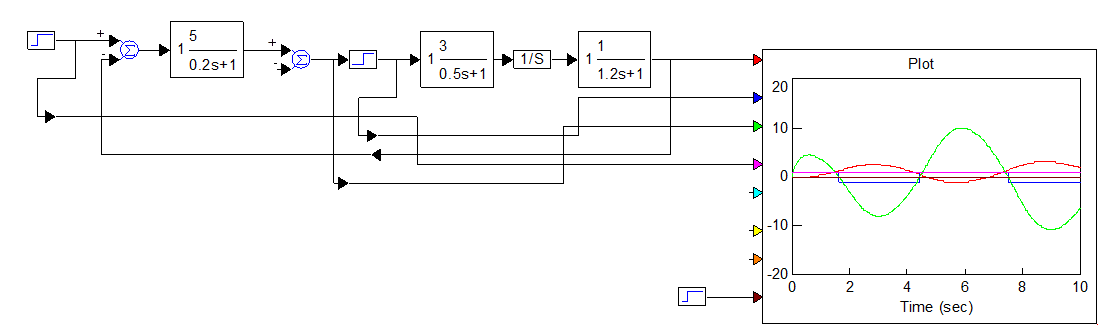
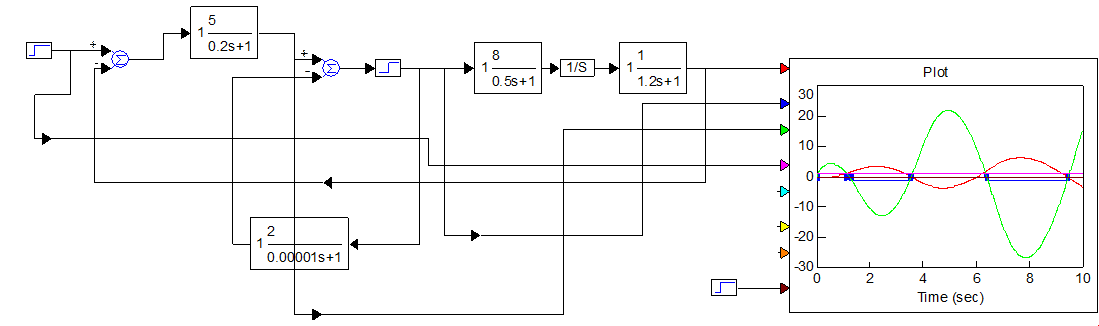
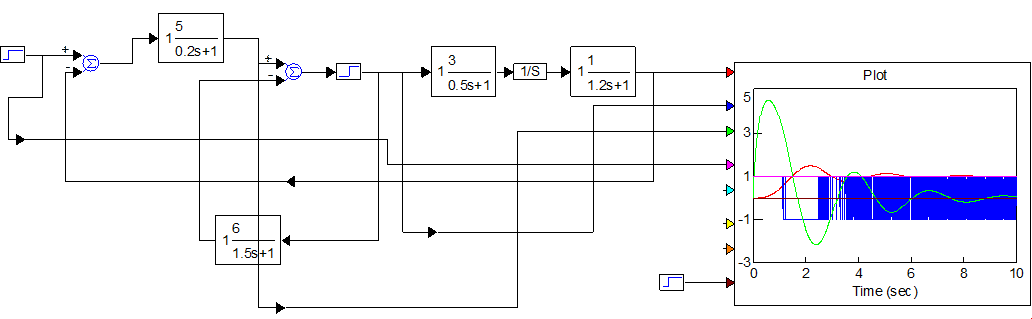
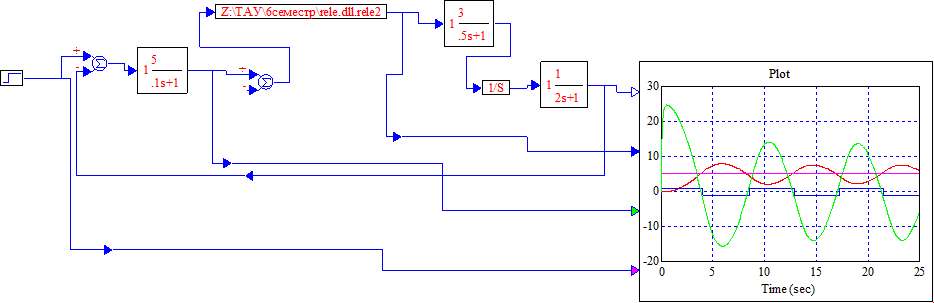
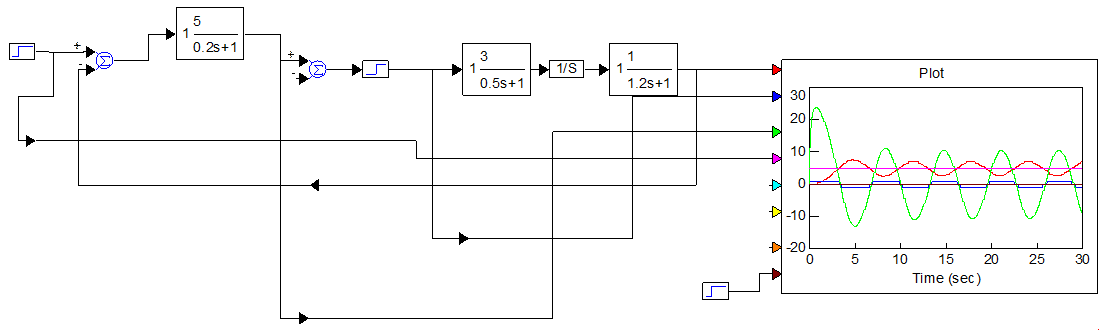
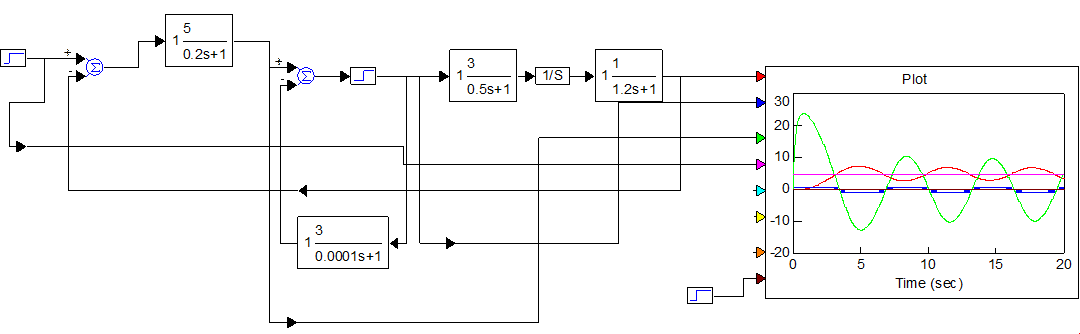
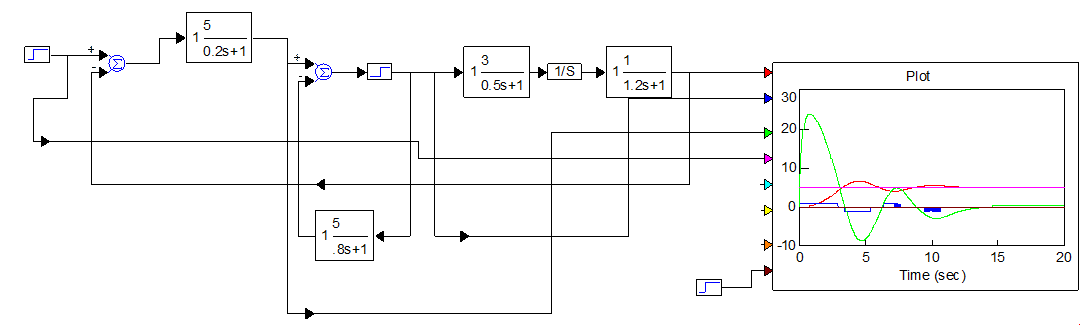
Рисунок 5.3 – Схема моделирования

НЭ:

а)                                                                                        

Рисунок 5.4 – Исследуемые нелинейные элементы

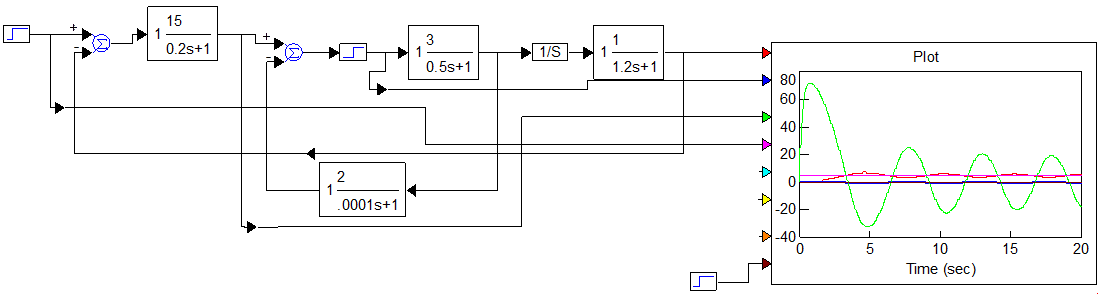
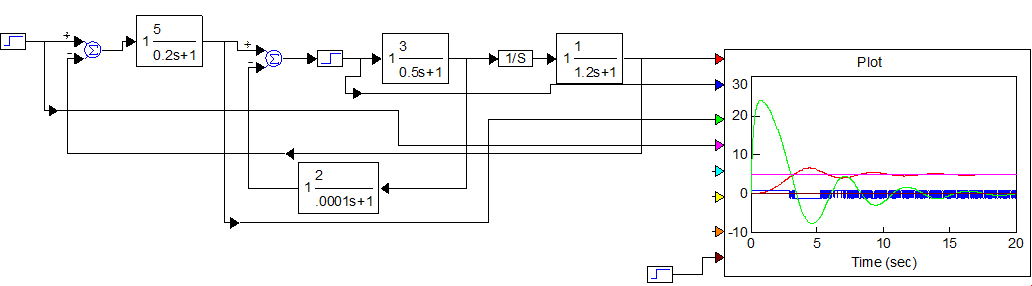
а=1

а=2

Зона нечувствительности 4

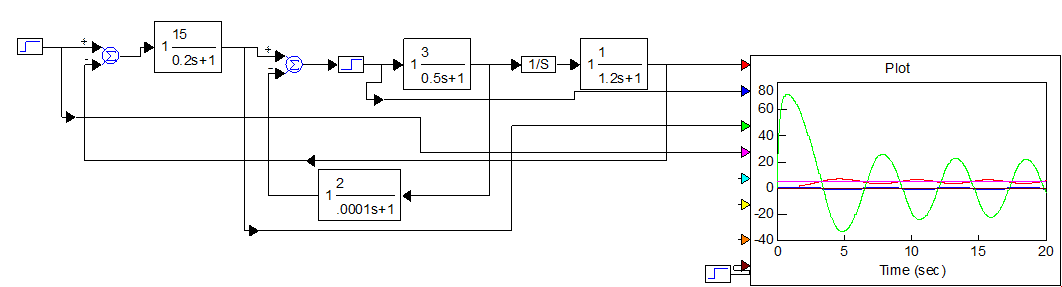
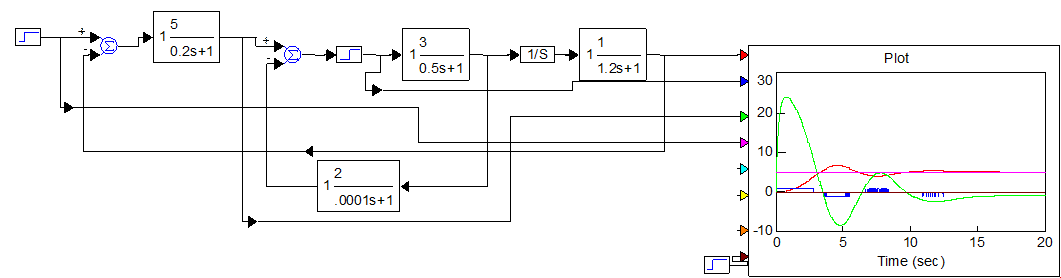
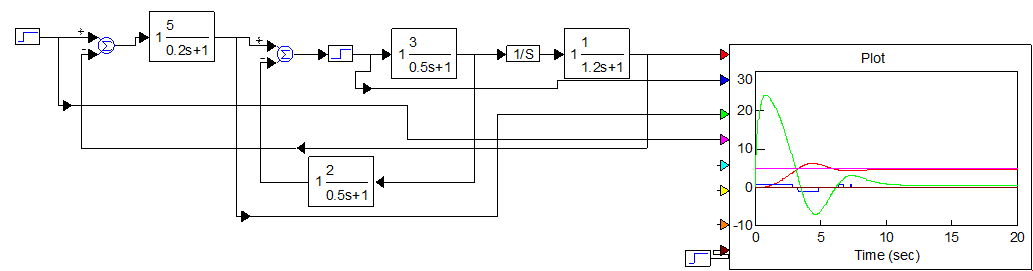
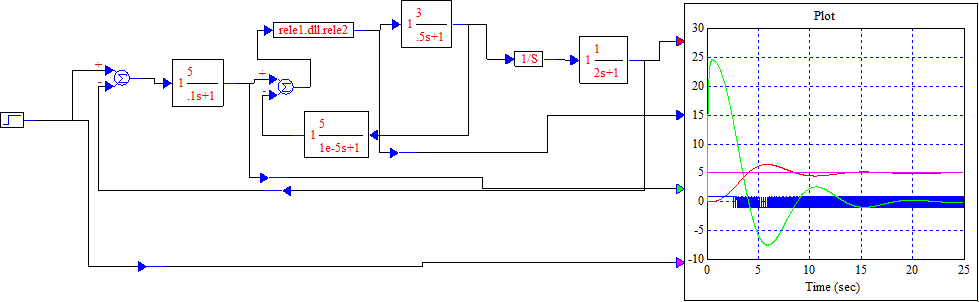
5. Исследовать вынужденное движение g(t)=5*1(t)

Wос(s)=Кос\(TосS+1) и  Wос(s)=S*Кос\(TосS+1).

6.  Выбрать оптимальные КУ и их параметры.

Содержание отчёта.

1. Схемы исследования.

2. Результаты исследования – указать на графиках ,  и их значения.

3. Построить зависимости () и (), найти  и , которые устраняют режим автоколебаний.

4. Рекомендации по коррекции нелинейных систем.