Линейные разностные уравнения с
постоянными коэффициентами.
Выражение:
(1)
называется разностным уравнением.
Здесь 
-
заданные постоянные коэффициенты, а 
- заданная
дискретная функция.
Уравнение (1) устанавливает связь между дискретной функцией и ее разностями.
Если воспользоваться:
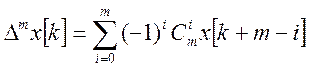(2)
То уравнение (1) представим в виде:
(3)
Где 
-
постоянные коэффициенты, связанные с формулой:
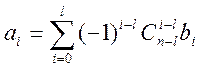(4)
Число n в выражении (3) – порядок разностного уравнения.
Дискретная функция 
, которая обращает разностное
уравнение (3) в тождество, называется решением разностного уравнения.
Если 
,
то получим однородное разностное уравнение:
(5)
Уравнение вида:
(6)
называется характеристическим уравнением заданного разностного уравнения. Общее решение разностного уравнения (3) состоит из двух частей:
1) Из общего решение соответствующего линейного однородного уравнения, которое зависит от n постоянных и определяется формулой:
(7)
2) Из частного решения
неоднородного разностного уравнения 
, которое
определяется видом правой части . И,
следовательно, общее решение линейного неоднородного разностного уравнения
определяется равенством:
(8)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
