БАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ, ТЕХНОЛОГИИ И УПРАВЛЕНИЯ
ФАКУЛЬТЕТ ИНЖИНЕРО – СТРОИТЕЛЬНЫЙ
ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ СТАЦИОНАРНЫХ
ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
Выполнили ст. гр. УИТ-41
Данилова В.А.
Принял доцент каф. УИТ
Скоробогатова Т.Н._______
«___»_______________2003
2003
СОДЕРЖАНИЕ
Задание 3
1 Преобразование структурной схемы САР 4
2 Критерии устойчивости 6
2.1 Критерий Гурвица 6
2.2 Критерий Льенара-Шипара 7
2.3 Критерий Рауса 7
2.4 Критерий Найквиста 8
2.5 Критерий Михайлова 10
2.6 D-разбиение 12
2.7 Устойчивость системы по методу Ляпунова 14
Вариант №55
Дана структурная схема САР вида рисунка 1, с передаточными функциями
звеньев: 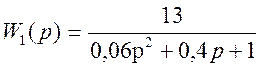 ,
, ![]() ,
,
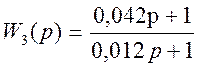 ,
, 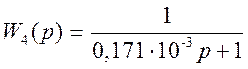 ,
,
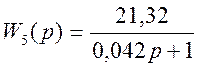 ,
, ![]() .
Необходимо проверить устойчивость системы по критериям: Гурвица, Льенара –
Шипара, Рауса, Михайлова, Найквиста, D-разбиения, Ляпунова, Шур - Кона.
.
Необходимо проверить устойчивость системы по критериям: Гурвица, Льенара –
Шипара, Рауса, Михайлова, Найквиста, D-разбиения, Ляпунова, Шур - Кона.
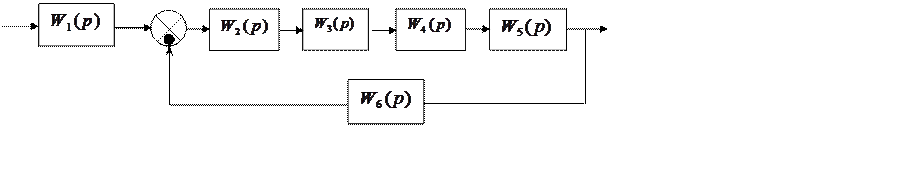 Рисунок 1
Рисунок 1
1 ПРЕОБРАЗОВАНИЕ СТРУКТУРНОЙ СХЕМЫ САР
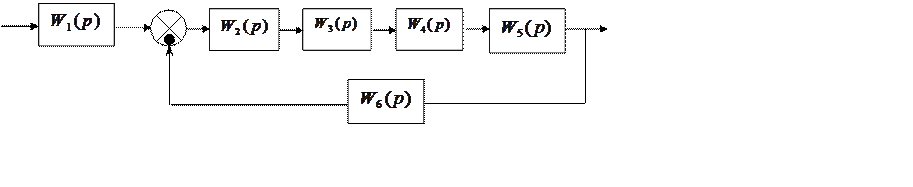 |
Рисунок 2
Звенья W2(p), W3(p), W4(p), W5(p) соединены последовательно, следовательно, имеем:
![]()
![]() ,
,
 .
.
В соответствии с данным преобразованием, структурная схема САУ примет вид:
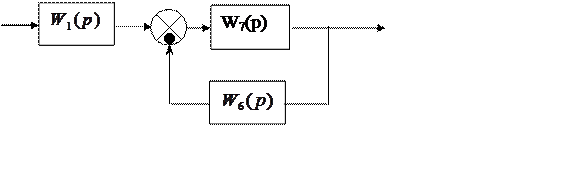
![]()
Рисунок 3
Звенья W6(p), W7(p) включены встречно – параллельно, следовательно:
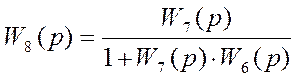 ,
,
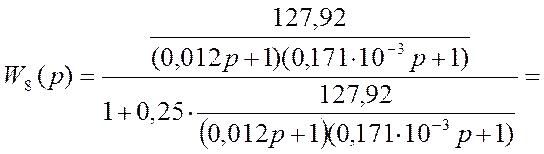
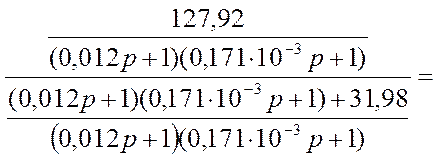
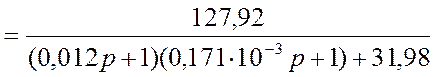 .
.
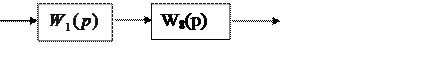 Тогда:
Тогда:
Рисунок 4
Исходя из схемы рисунка 4, по правилу преобразования структурных схем, получим передаточную функцию системы:
![]() ,
,
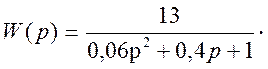
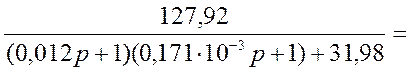
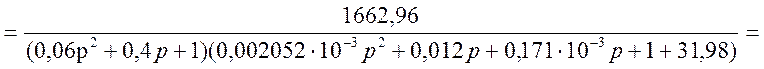
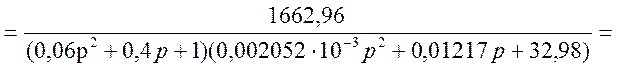
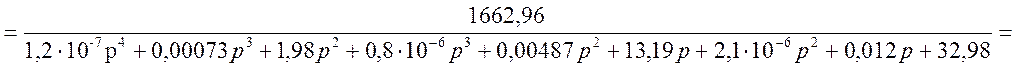
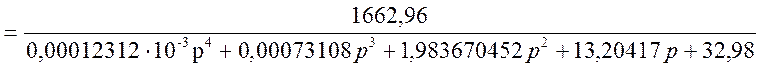 .
.
 Получим:
Получим:
Рисунок 5
Т.е. передаточная функция системы имеет вид:
![]()
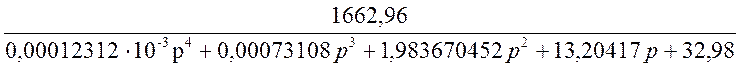 .
.
2 КРИТЕРИИ УСТОЙЧИВОСТИ
Запишем характеристическое уравнение для рассматриваемой системы, получим:
![]() .
.
Характеристическое уравнение является уравнением 4-го порядка, коэффициенты которого положительны, а значит и корни все левые, из чего можно сделать вывод, что необходимое условие устойчивости выполняется.
2.1 КРИТЕРИЙ ГУРВИЦА
Составим
определители Гурвица из коэффициентов характеристического уравнения:![]() ;
;![]() ;
;![]() ;
;![]() ;
; ![]() .
.
|
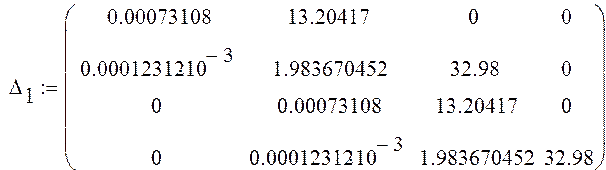
|
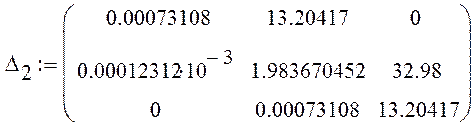
|
|
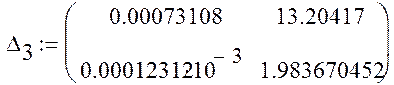
![]()
Согласно критерию Гурвица, система устойчива, т.к.
определители имеют одинаковые знаки с коэффициентом ![]() .
.
2.2 КРИТЕРИЙ ЛЬЕНАРА – ШИПАРА
Данная
нам система является устойчивой, т.к. при положительности коэффициентов ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() характеристического
уравнения все определители Гурвица с нечетным индексом положительны.
характеристического
уравнения все определители Гурвица с нечетным индексом положительны.
Таким образом, условие устойчивости можно записать следующим образом:
![]() ;
; ![]() .
.
2.3 КРИТЕРИЙ РАУСА
Устойчивость системы по критерию Рауса определяется из таблицы, элементами которой являются коэффициенты, вычисляемые по следующим формулам:
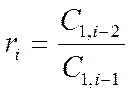 ;
;
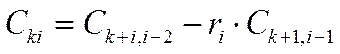 .
.
Таблица 1
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.