Исследование устойчивости стационарных линейных систем автоматического регулирования, страница 2

Коэффициент	Номер строки i	Номер столбца к
		к=1	к=2	к=3
-	1	a0=C11	a2=C21	a4=C31
-	2	a1=C12	a3=C22	a5=C32=0
	3
	4
	5
	6

          Данная нам система является устойчивой, т.к. коэффициент a₀, а также все коэффициенты первого столбца таблицы Рауса являются положительными.

2.4 КРИТЕРИЙ НАЙКВИСТА

Если СУ устойчива в разомкнутом состоянии, то для того, чтобы она была устойчива в замкнутом, необходимо и достаточно, чтобы кривая АФЧХ   разомкнутой системы при изменении  от 0 до  не будет охватывать точку .

          Представим передаточную функцию в комплексной форме, т.е. .

.

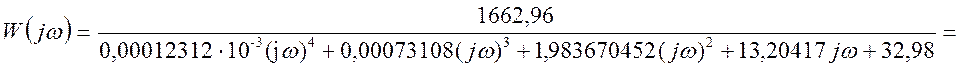
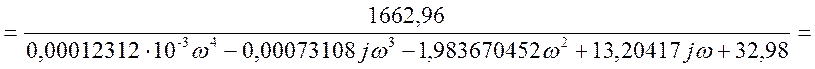
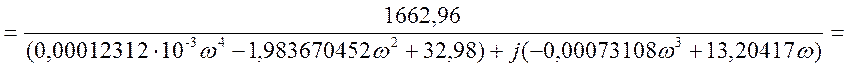
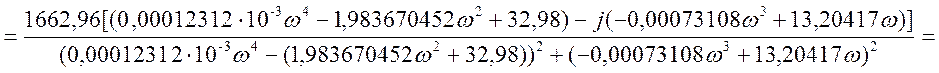
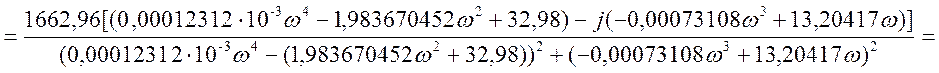
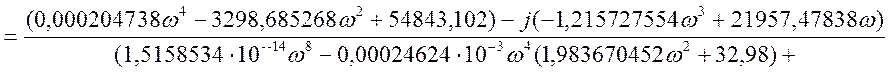
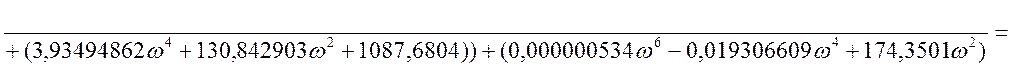
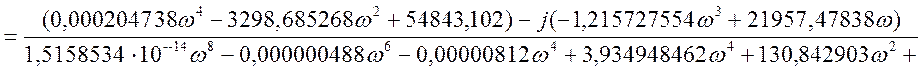
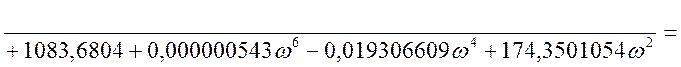
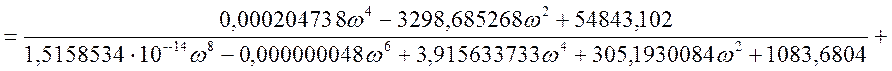
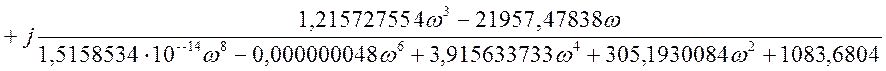Получим действительную и мнимую части:

;

.

;

;

          Построим кривую, но сначала проведем следующий анализ:

;

.

    

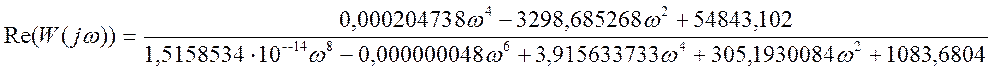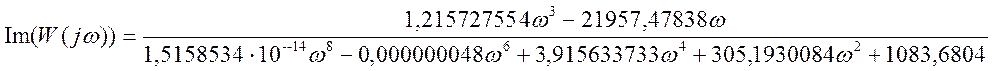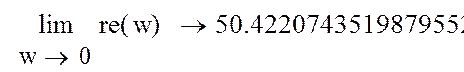
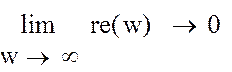
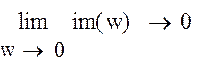
Получим:

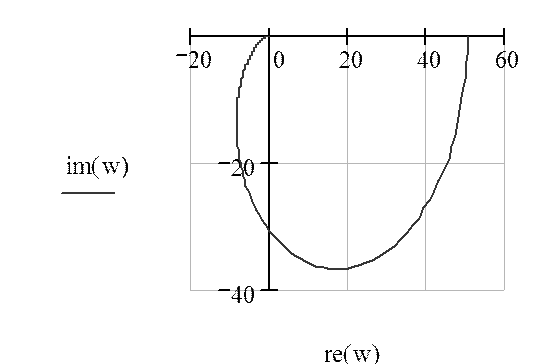
Рисунок 6

          По условию устойчивости Найквиста, кривая не должна охватывать точку , увеличим масштаб рисунка 6 для большей наглядности.

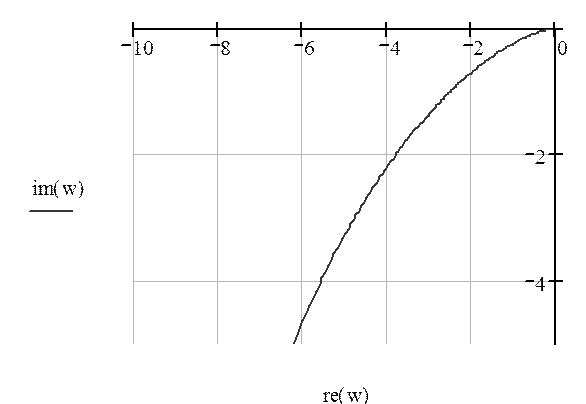
Рисунок 7

          Из рисунка 7 видно, что данная нам система устойчива.

2.5 КРИТЕРИЙ МИХАЙЛОВА

          Согласно данному критерию для того, чтобы САУ была устойчивой необходимо и достаточно, чтобы вектор кривой Михайлова   при изменении частоты  от 0 до , повернулся в положительном направлении вокруг начала координат на угол , где - порядок характеристического уравнения.

          Характеристическое уравнение рассматриваемой системы имеет вид:

          Заменим на , получим:

          Представим характеристический полином  в виде:

;

;

.

;

          Построим кривую Михайлова, но сначала проведем следующий анализ:

;

;

.

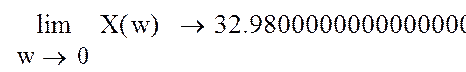
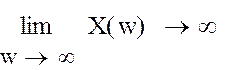
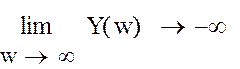
          Графики построены с постепенным увеличением масштаба, т.е.:

Рисунок 8,а

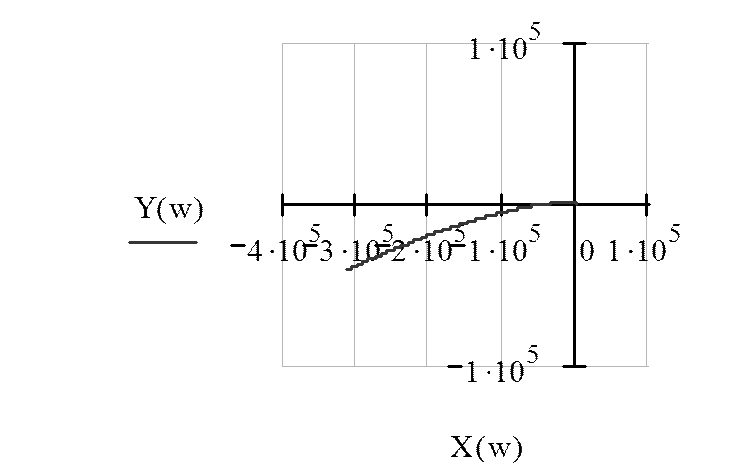
Рисунок 8,б

                     

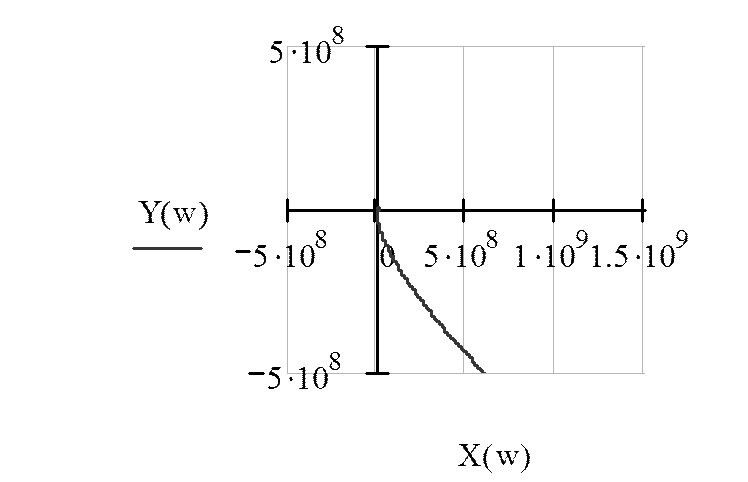
Рисунок 8, в

Из рисунка 8,в видно, что вектор кривой Михайлова поворачивается на угол 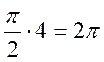, т.е. уходит в бесконечность в 4 квадранте, следовательно, система устойчива.

2.6 D-РАЗБИЕНИЕ

          Выполним D-разбиение по одному параметру.

Пусть 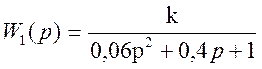 , тогда передаточная функция системы примет вид:

.

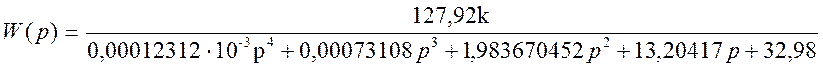          Охватим всю систему обратной отрицательной связью, т.е.:

 

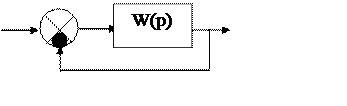Рисунок 9

          Следовательно, общая передаточная функция вычисляется по формуле:

;

.

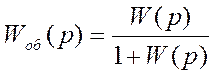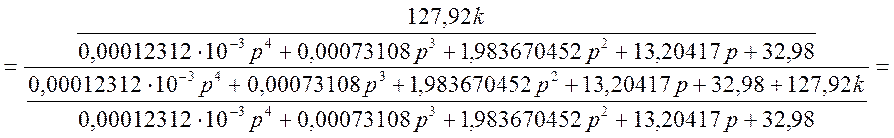
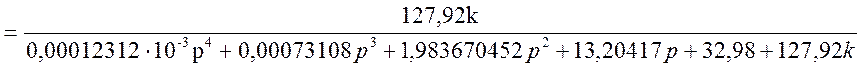          Т.е.:

.

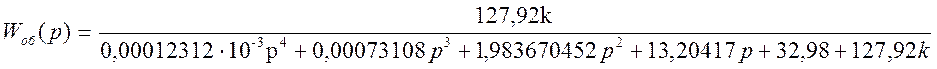          Тогда характеристическое уравнение имеет вид:

.

В последнем выражении произведем замену  и выразим из него коэффициент k:

;

.

Выразим действительную и мнимую части, а затем построим кривую D – разбиения по параметру k.

№2

№1

D(1)

D(1)

D(0)

( k )

( k )

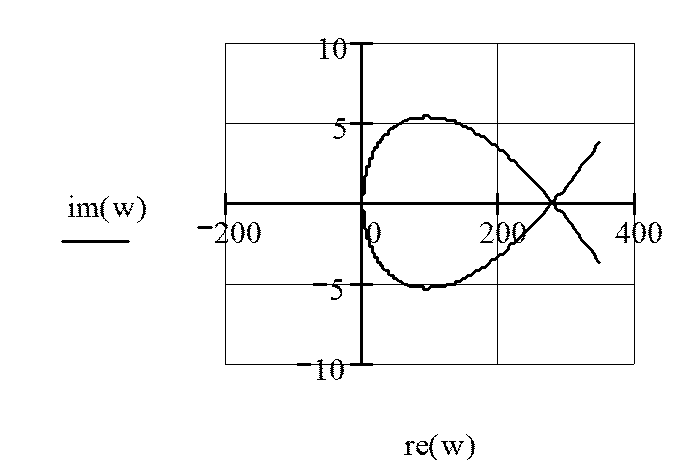
Рисунок 10

          Переходу по стрелке №1 соответствует уменьшение правых корней на единицу, переходу по стрелке №2 соответствует уменьшение правых корней на единицу. В результате переходов попадаем в область, где число правых корней минимально, т.е. в область D(o).

          Область D(o) является областью подозрительной на область устойчивости, и требует проверки.

          Выберем из области D(o) произвольное значение параметра k, например k=100, и подставим в характеристическое уравнение, получим:

.

          Выполним проверку устойчивости по критерию Гурвица.

Составим определители Гурвица из коэффициентов характеристического уравнения:;;;; .

=23,66;

=0,018;

;

	.

 

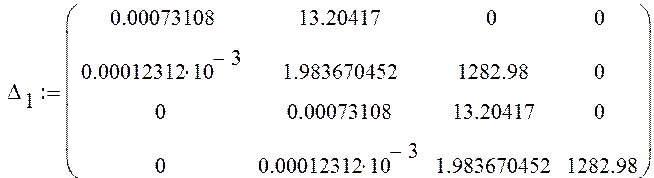
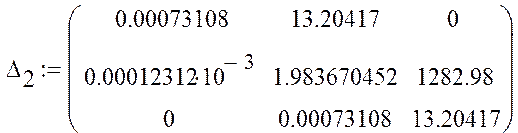
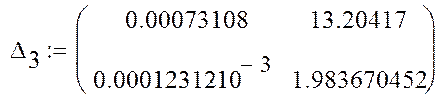
Так как определители положительны при положительном а₀, то САУ является устойчивой.

2.7 УСТОЙЧИВОСТЬ СИСТЕМЫ ПО МЕТОДУ ЛЯПУНОВА

          По критерию устойчивости Ляпунова, система устойчива, если для нее выполняется следующее условие: .

Т.е. для того чтобы САУ была устойчива необходимо и достаточно, чтобы все корни характеристического уравнения имели отрицательные вещественные части.

.

Определим корни характеристического уравнения:

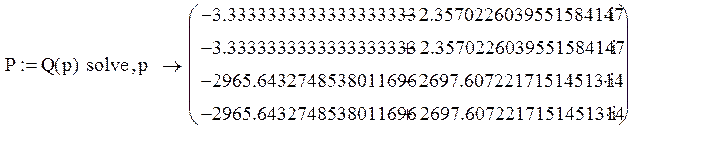
Так как все корни характеристического уравнения лежат с лева от мнимой оси (левые корни) и имеют отрицательную вещественную часть, то САУ будет устойчивой.