БАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ, ТЕХНОЛОГИИ И УПРАВЛЕНИЯ
ФАКУЛЬТЕТ ИНЖЕНЕРНО-СТРОИТЕЛЬНЫЙ
КАФЕДРА УИТ
Теория автоматического управления
Исследование устойчивости линейных и нелинейных систем
автоматического управления
Сербаев В.В.
Скоробогатова Т.Н. _______
“______” ___________2003
![]() 2003
2003
СОДЕРЖАНИЕ
Введение 3
Часть 1 Линейная САУ 4
1 Техническое задание 4
2 Упрощение структурной схемы САУ 4
3 Анализ устойчивости САУ 6
4 Построение переходных характеристик 7
4.1 Построение АЧХ 8
4.2 Построение ФЧХ 8
4.3 Построение АФЧХ, ЛАЧХ и ЛФЧХ системы 9
4.4 Построение графика переходного процесса 10
5 Анализ качества управления 11
Вывод 12
Часть 2 Нелинейная САУ 13
1 Техническое задание 13
2 Упрощение структурной схемы САУ 13
3 Построение фазового портрета 14
Вывод 16
Список используемой литературы 17
Введение
Построение систем автоматического управления требует создания качественных регуляторов. Данная задача является первостепенной в любой САУ. Построение качественного регулятора требует создание такой системы, которая была бы устойчивой при некотором изменении внешних факторов и внутренних процессов.
В выполняемой курсовой работе предлагается исследовать линейную и нелинейную систему и ознакомится с влиянием нелинейных узлов на работу регулятора.
В ходе контрольной работы будет проведено упрощение системы, определена ее устойчивость и найдены основные характеристики качества управления. Данные операции будут проделаны для линейной и нелинейной САУ. Будет показано, как влияет введение в регулятор нелинейных узлов, и определен положительный (отрицательный фактор) данных узлов в системе. В ходе выполнения курсовой работы будет построен фазовый портрет, который является отражением работы нелинейной системы. Будет сделан вывод по каждой из систем и внесены предложения.
Вариант № 44
ИССЛЕДОВАНИЕ ЛИНЕЙНОЙ САУ
1 Техническое задание
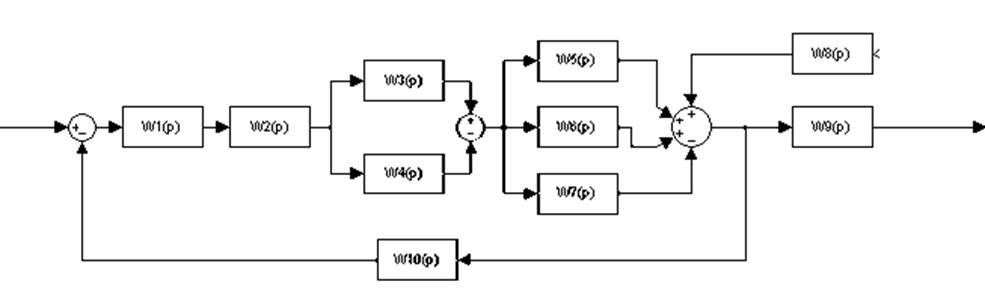 Исходная Рисунок САУ изображена на рисунке 1
Исходная Рисунок САУ изображена на рисунке 1
Рисунок 1
Передаточные функции звеньев:
W1(p)=38; W2(p)=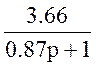 ; W3(p)=0.74; W4(p)=0.74; W5(p)=
; W3(p)=0.74; W4(p)=0.74; W5(p)=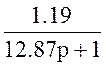 ; W6(p)=
; W6(p)=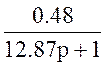 ;
;
W7(p)=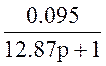 ; W8(p)=
; W8(p)=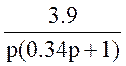 ;
W9(p)=16.3; W10(p)=
;
W9(p)=16.3; W10(p)=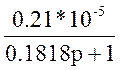
2 Упрощение структурной схемы САУ
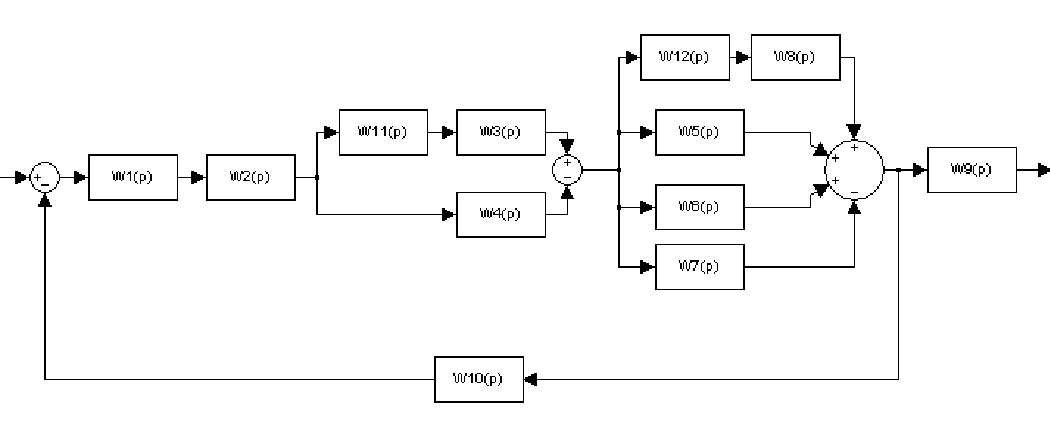 Требуется изменить передаточную функцию W3(p)
или W4(p),
чтобы суммарная функция была ненулевой. Требуется добавить звено к W8(p) (
дифференцирующее звено), чтобы снять интегрирующую составляющую, тем самым
итоговое звено будет устойчивым. Проведя преобразования, получим схему 2.
Требуется изменить передаточную функцию W3(p)
или W4(p),
чтобы суммарная функция была ненулевой. Требуется добавить звено к W8(p) (
дифференцирующее звено), чтобы снять интегрирующую составляющую, тем самым
итоговое звено будет устойчивым. Проведя преобразования, получим схему 2.
Рисунок 2
Обозначение: W11(p)=2, W12(p)=p.
Упростим:
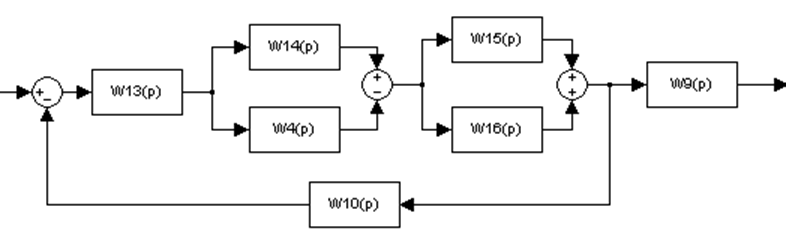
Рисунок 3
Обозначение: W13(p)=W1(p)*W2(p)= 38*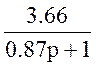 =
=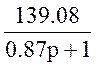
W14(p)=W11(p)*W3(p)=2*0.74=1.48
W15(p)=W12(p)*W8(p)=p*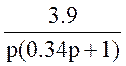 =
=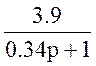
W16(p)=W5(p)+W6(p)-W7(p)=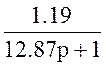 +
+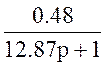 -
-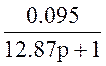 =
=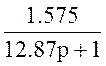
Упростим далее:
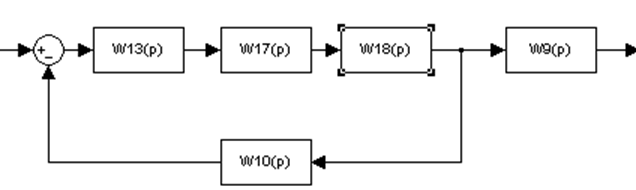
Рисунок 4
Обозначение: W17(p)=W14(p)-W4(p)=1.48-0.74=0.74
W18(p)=W15(p)+W16(p)=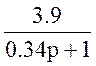 +
+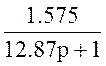 =
=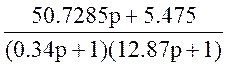
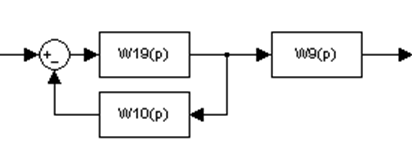
Рисунок 5
Обозначение: W19(p)=W13(p)*W17(p)*W18(p)=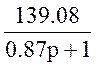 *0.74*
*0.74*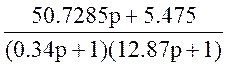 =
=
=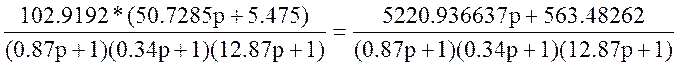
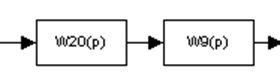
Рисунок 6
Обозначение: W20(p)=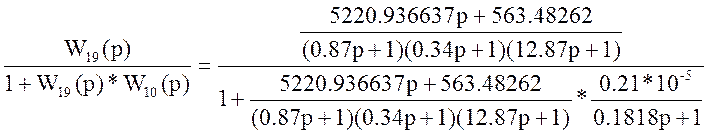 =
=
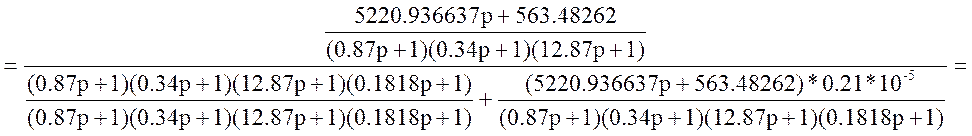
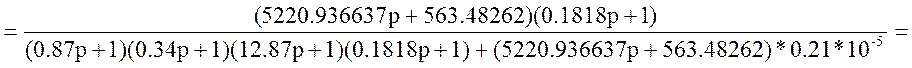
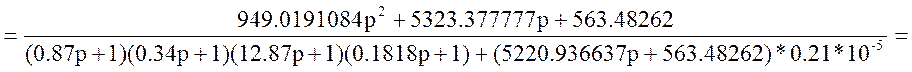
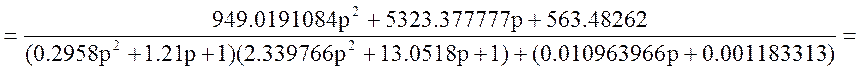
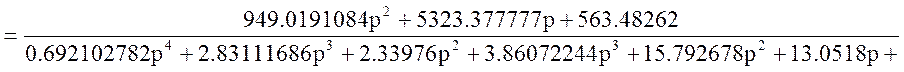
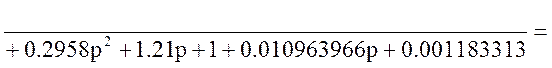
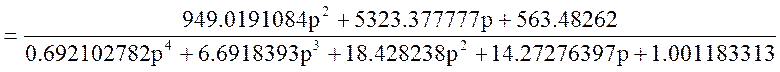
Упростим схему:
 |
Рисунок 7
Обозначение: W21(p)=W20(p)*W9(p)= 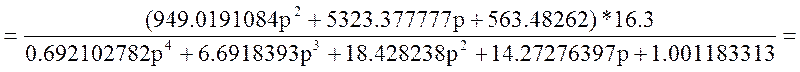
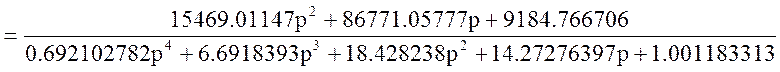
3 Анализ устойчивости САУ
Запишем характеристическое уравнение системы:
![]()
a0=0.692102782; a1=6.6918393; a2=18.428238; a3=14.27276397; a4=1.001183313
Теперь можно составить главный определитель Гурвица:
|
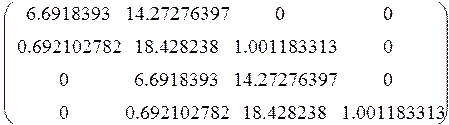
Посчитаем определители:
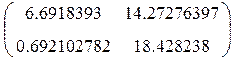 1.
1. ![]() (6.6918393)=6.6918393
(6.6918393)=6.6918393
2. ![]() =113.441
=113.441
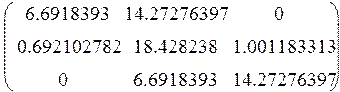 |
3. ![]() =1574
=1574
Согласно критерию Гурвица, система устойчива, т.к. определители имеют один знак с a0.
4 Построение переходных характеристик
Для большинства характеристик потребуется определить вещественную и мнимую части комплексной передаточной функции, что и проделаем.
Исходная передаточная функция имеет вид:
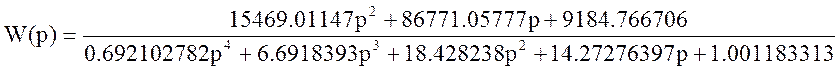
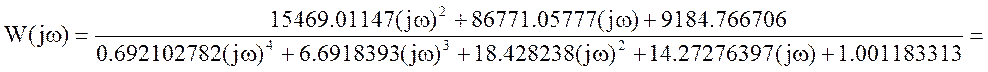
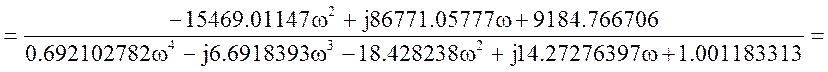
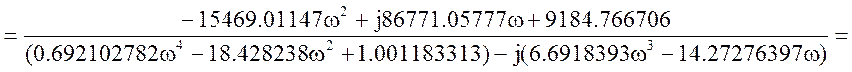
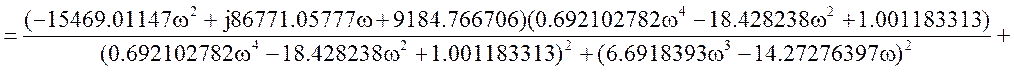
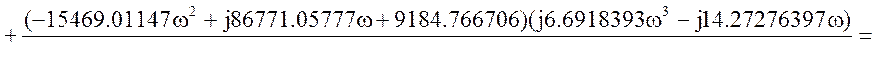
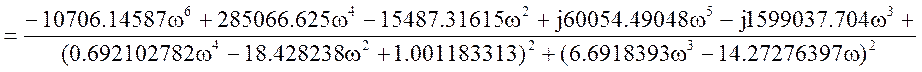
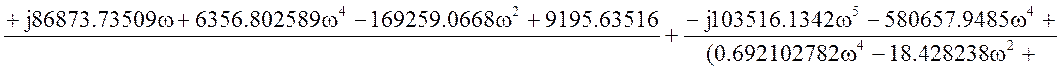
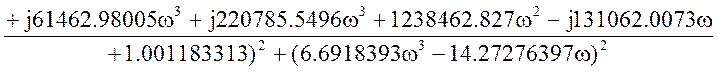
Соберем коэффициенты и выделим вещественную и мнимую части.
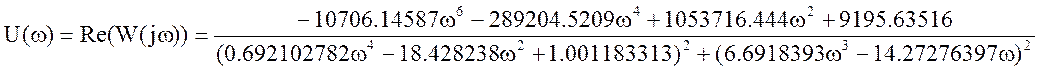
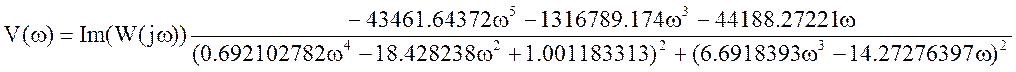
4.1 Построение АЧХ
АЧХ системы определяется по формуле ![]() Исходя из представленных формул АЧХ
примет вид:
Исходя из представленных формул АЧХ
примет вид:
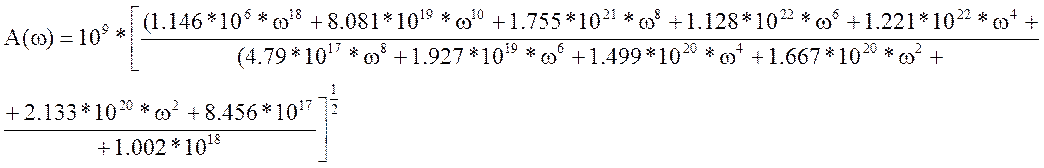
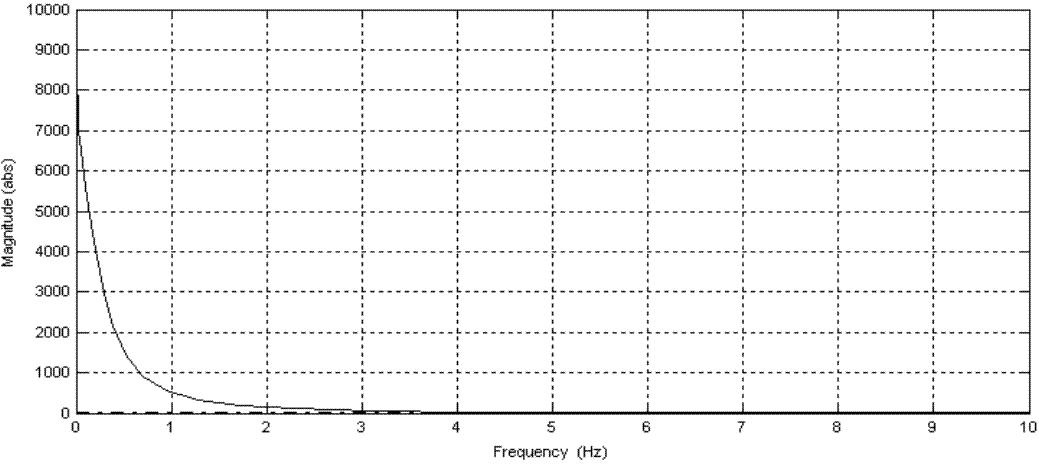 |
Рисунок 8
4.2 Построение ФЧХ
Фазовая характеристика находится по формуле:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.