Привод ленточного конвейера с прямозубым цилиндрическим редуктором, страница 7

Определение размеров зубчатого колеса

  

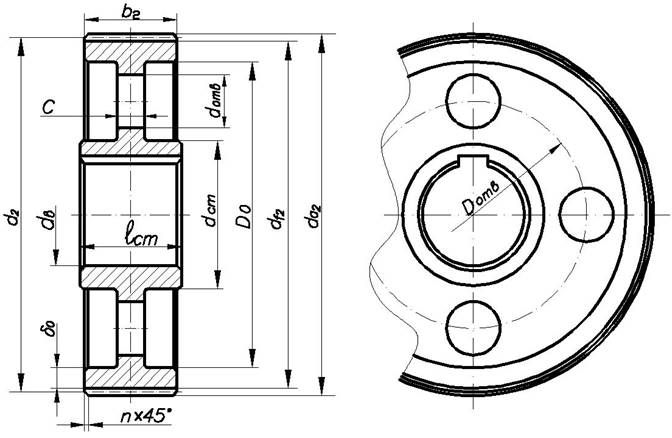
Диаметр ступицы d_cm :

d_cm ≈ (1,5…1,6)d₇ =                                                          мм где d₇  - диаметр вала (см. рис.4), длина ступицы l_cm:

l_cm≈ (1,0…1,2) d₇ =                                                            мм толщина обода δ₀ = (2,5…4,0)m, но не менее 8 мм:

δ₀ = (2,5…4,0)m =                                                              мм толщина диска С = 0,3b₂, где b₂ – ширина колеса:

С = 0,3b₂ =                                                                                   мм

Диаметр окружности центров D_отв:

D_отв = 0,5(D₀ + d_cm) =                                                                мм

Диаметр отверстий d_отв:

d_отв ≈ 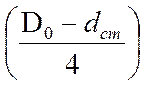   =                                                        мм 

Фаска:

n ≈ 0,5m =                                                                         мм

Внутренний диаметр обода D₀ :

D₀ = d_f2 - 2δ₀ =                                                                            мм

где d_f2  -  диаметр впадин зубьев колеса (см. п.20 расчёта)

Значения d₂ , d_f2 и d_a2  см. п. 20 расчёта

Проверочный расчет тихоходного вала на прочность и выносливость

Определение усилий в зацеплении и сил, действующих на вал

Окружную силу F_t2 определяем по формуле:

F_t2 =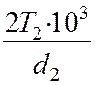  =                                                            Н,

где d₂ мм- делительный диаметр колеса (см. п. 20 расчета)!

Радиальную силу F_r2 определяем по формуле:

F_r2 =F_t2· tg= F_t2·tg20°= F_t2·0,364=            · =                    Н,

Нагрузка на концевом участке вала от муфты определяем по формуле :

F_м2 = 125· = 125 ·      =                    Н.

Схема нагружения тихоходного вала (рис. 5)

Для определения усилий, действующих на тихоходный вал, необходимо вычертить схему зацепления в аксонометрии, а направление вращения валов выбрать в зависимости от направления движения конвейера (из задания).

Определение реакций в опорах

 Горизонтальная плоскость

В этой плоскости действуют силы F_r2 .      

Реакция в точке А (R_А^г):

∑М_с = 0 ⇒ – F_r2 · b + R_А^г · (a + b) = 0

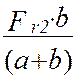R_А^г =  =                                                          Н.

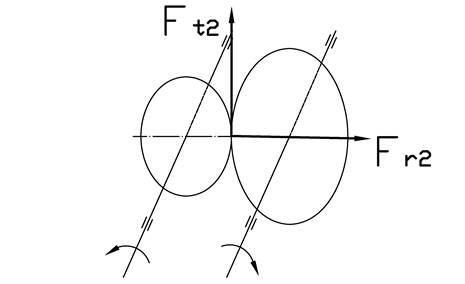
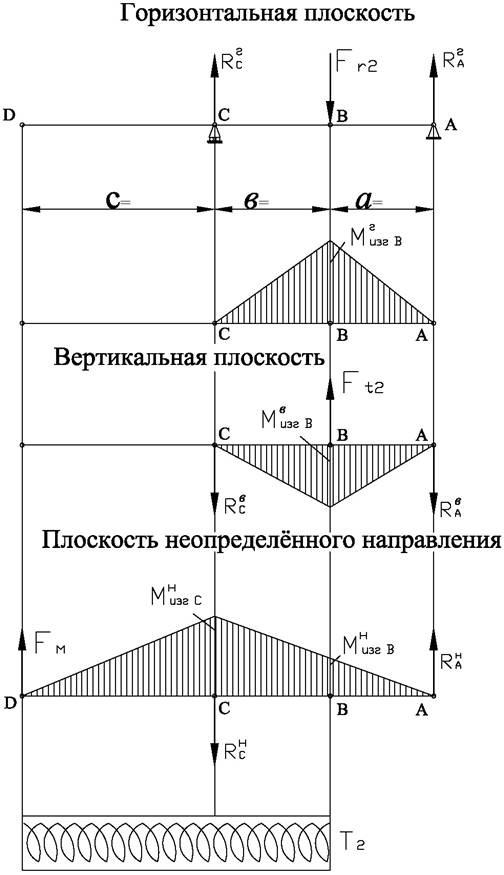
Рис. 5. Схема нагружения тихоходного вала

Реакция от силы F_r2 в точке С (R_С^г):

∑М_А = 0 ⇒ –· (a + b) + F_r2 · a = 0

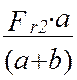 ==                                                                             Н.

Проверка: ∑F_y = 0 ⇒ R_С^г – F_r2 + R_A^г = 0

        ∑F_y=                                              = 0.

Строим эпюру изгибающих моментов в горизонтальной плоскости (рис. 5).

Изгибающий момент в точке В в горизонтальной плоскости:

        =  · а =                                     Н·м.

    Вертикальная плоскость

В этой плоскости действует сила F_t2.

Реакция от силы F_t2 в точке А (R_A^в):

∑М _с = 0 ⇒ F_t2 · b – R_A^в · (a + b) = 0

R_A^в = 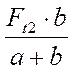 =                                         Н

Реакция от силы F_t2 в точке С ():

∑М _А = 0 ⇒ R_С ^в · (a + b) – F_t2 · а = 0

R_С^в = 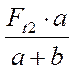 =                                            Н

Проверка: ∑F_y= 0 ⇒ –R_A^в + F_t2 –  = 0

 ∑F_y =                                   = 0

Строим эпюру изгибающих моментов в вертикальной плоскости (рис. 5).

Изгибающий момент в точке В от силы F_t2 ():

= R_A^в · a =                                     Н·м.

 Плоскость неопределенного направления

Реакция от силы FМ₂  в точке А (R_A ^н):

Значение FМ₂  см. выше.

∑М _с = 0 ⇒ – FМ₂ · с + R_A ^н · (a + b) = 0

R_A ^н = 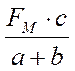 =                                               Н

Реакция от силы FМ₂ в точке С ():

∑М _А = 0 ⇒  · (a + b) – FМ₂ ·(а + b + c) = 0

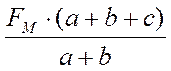 =   =                                                           Н

Проверка: ∑F_y = 0 ⇒ FМ₂ –  +  = 0

∑F_y                                            = 0

Строим эпюру изгибающих моментов от силы F_М в плоскости неопределенного направления (рис. 5).

Изгибающий момент в точке В от силы FМ₂ ():

 =  · a =                                         Н·м.