Привод ленточного конвейера с прямозубым цилиндрическим редуктором, страница 4

24. Эквивалентное число циклов нагружения зубьев колеса:

N_{FЕ 2} = 60 ∙ п₂ ∙ Т_FЕ =                                                     циклов

Таким образом, передача работает при постоянной нагрузке, т.к.

N_{FЕ 2} > N_FG = 4 ∙ 10⁶ циклов   и 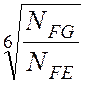           = 1

25. Допускаемые напряжения изгиба [σ]_F:

Предел изгибной выносливости для зубьев шестерни σ_{Flim 1} :

       σ_{Flim 1} = 1,8 ∙ НВ₁ =                                                       МПа

Предел изгибной выносливости для зубьев колеса σ_Flim2:

σ_{Flim 2} = 1,8 ∙ НВ₂  =                                                      МПа

где НВ₁ и НВ₂ см. п.11 расчета

Допускаемые напряжения изгиба для шестерни:

        [σ]_F1 = 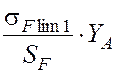 =                                                    МПа где коэффициент безопасности S_F = 1,75 , а коэффициент

        режима работы для нереверсивной передачи Y_A = 1.

Допускаемые напряжения изгиба для колеса:

        [σ]_F2 = 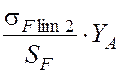 =                                                    МПа

26. Окружное усилие на колесе:

F_t2 = 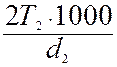 =                                                                  Н

        (где Т₂ Нм, см. п.7, а d₂  мм – см. п.20 расчета)

27.   Коэффициент формы зубьев при расчете на изгиб по местным напряжениям Y_FS для прямозубых передач определяют в зависимости    от Z из табл. 10 стр. 32 :

         У_FS1 =                                (при Z₁=          )                               

               У_FS2 =(при Z₂=          ) 

Напряжения изгиба для зубьев прямозубых передач.

Расчет на изгиб производится для той зубчатки, у которой   

отношение  =  меньше.

Для шестерни:  =                                                   МПа

Для колес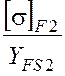а:  =                                                        МПа

Для ………………..это отношение меньше, поэтому расчет   ведем по  зубу   ………..           .

Коэффициент нагрузки при расчете на изгиб предварительно  принимаем К_F = 1,3     

            Напряжение изгиба для зубьев колеса:

        σ_F2 = 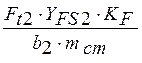=                                                              МПа

  Внимание! Размеры b₂ и m_cm подставляются в мм!

Поскольку  σ_F2 =                 МПа < [σ]_F2 =               МПа, то условие    

     прочности выполняется.

28. Расчет на кратковременные перегрузки.

•  По контактным напряжениям

Максимальное допускаемое контактное напряжение при     

пусковой перегрузке:

      [σ] _{Н max2} = 2,8 ∙ σ_т =                                                             МПа

       где σ_т =           МПа для материала колеса (см. п.10 расчета)

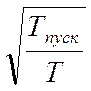       σ_{Н max2} =  σ_Н2 ∙ =                                                  МПа

       где σ_Н2 см п.21 расчета

Поскольку  σ_{Н max2}  =             МПа < [σ]_{Н max2} =             МПа, то    

условие прочности выполняется.

•  По напряжениям изгиба

Максимальное допускаемое напряжение изгиба при пусковой  перегрузке:

        [σ]_{F max 2} = 2,74 ∙ НВ₂ =                                           МПа, где

где НВ₂ см п.11 расчета

Максимальное напряжение изгиба при пусковой перегрузке:

        σ_{F max}  = σ_F ∙ 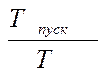 =                                            МПа

отношение 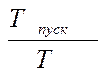 дано в задании, а σ_F2  см п.27 расчета.

Поскольку σ_{F max2}  =           МПа < [σ]_{F max2} =           МПа, то условие прочности выполняется.

эскизная компоновка редуктора

Вычерчивание контура зубчатых колес и стенок редуктора

После определения геометрических размеров передачи приступаем к предварительному конструированию редуктора. Для этого на миллиметровке формата А1 делаем эскизную компоновку двух проекций редуктора. Вначале наносим осевые линии межосевого расстояния а_{w ст} , затем размеры шестерни и колеса – d₁, d₂, b₁, b₂ (п.14 и п.20 расчета). Размер Δ – зазор между торцем шестерни и внутренней стенкой редуктора выбираем в пределах 8–10 мм (рис. 2).