Проектирование активных фильтров на операционных усилителях, страница 6

В узкой полосе пропускания, когда, симметрия функции ПФ приближается к арифметической [Df_ср = 0,5(f_пв + f_пн)] и соотношения (16) упрощаются:

.         (15)

Точность соотношения (15) возрастает с уменьшением полосы пропускания и достаточна для практики при DW = 0,2 - 0,4 [3].

При дробной аппроксимации аппроксимирующая функция характеризуется не только полюсами, но и нулями передачи. Поскольку нули передачи преобразуют по тому же закону, что и полюсы, то подставляя в соотношение (13) нули Z_нj = ±jW_zнj НЧ – функции изображения, получим нули ПФ

     ; ,            (16)

где

,            (17)

.            (18)

6.  По найденным полюсам определяются физические параметры звеньев W₀ и l в соответствии с соотношениями (11) и (12). Как видно, порядок передаточной функции РФ удваивается в сравнении с НЧ-функцией-изображения;

7.  Переход от НЧ–функции изображения к синтезируемой функции ПФ завершается денормированием по (9) частот нулей передачи W_zн, W_zв и собственных частот звеньев W₀.

Построение полосно-задерживающей (ПЗ) функции РФ с помощью НЧ-изображения выполняетсяс помощью преобразования [1]

            ,                                     (19)

где S – комплексная частота НЧ–функции изображения;

p= jW – комплексная частота ПП-функции;

DW = (f_зв – f_зн)/f_ср - нормированная полоса заграждения РФ.

Порядок преобразования тот же самый, что и в случае для ПФ, только:

В пункте 3: полосе частот (f_пв – f_пн) соответствует нормированная граничная частота полосы задержания НЧ–функции изображения

,                       (20)

а нормированная граничная частота полосы пропускания НЧ–функции изображения  остаётся прежней;

В пункте 4: при обратном преобразовании, решая (19) относительно p, находим полюсы РФ из выражения

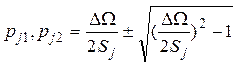,                        (21)

отсюда

,

(22)

, где 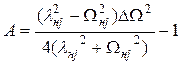; ; 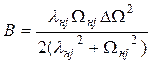l_{нj и} W_нj – действительная и мнимая части j–го полюса НЧ–функции изображения. Нули РФ находятся также из (21).

Порядок передаточной функции РФ удваивается в сравнении с НЧ-функцией-изображения.

2.3. Реализация активных фильтров на операционных усилителях

Очередной задачей синтеза фильтров является реализация найденной аппроксимирующей функции, т.е. определение на ее основе структурной (функциональной) схемы устройства, модуль коэффициента передачи которой удовлетворяет предъявленный техническим требованиям и наилучшим образом приближается к идеальней АЧХ. Решения этой задачи неоднозначно, так как одну и ту же функцию передачи может иметь множество физически реализуемых цепей. Поэтому на этом этапе проектирования (синтеза) следует выбрать конкретную электрическую схему, которая наилучшим образом реализует найденную аппроксимирующую функцию. В качестве критерия оптимальности может служить минимум числа элементов схемы, минимум чувствительности характеристик цепи к изменению во времени ее элементов и т.д.

Далее следует реализация фильтров на основе выбранной элементной базе.

Данную реализацию можно осуществить на различной элементной базе. Например, он может состоять из пассивных LCR или RC-элементов, а также из совокупности пассивных RC-элементов и активных элементов. Тенденции развития электроники сегодня таковы, что требуется создание фильтров, у которых отсутствуют индуктивные элементы. Это необходимо при работе на очень низких частотах (сейсмография, гидролокация, биолокация и т.д.), когда использование LCизбирательных цепей значительно увеличивает габариты фильтра (LC = 1/4p²f²), a также при микроминиатюризации аппаратуры, т.е. ее реализации на микросхемах. Применение же навесных индуктивных элементов сводит на нет преимущества интегральной элементной базы. По этим причинам получили распространение частотно-избирательные усилители с RC - цепями.

С помощью фильтра, построенного на базе пассивных RC и активных элементов можно получить, все характеристики, которые обеспечиваются RLC цепями. Поэтому такие фильтры, называемые активными RC-цепями (ARC-цепями), получили широкое распространение.