Проектирование активных фильтров на операционных усилителях, страница 3

где U_вых(p), U_вх(p) – комплексные напряжения на выходе и входе электрической цепи; b_i(i=0,…,m), a_j(j=0,…,n-1) – вещественные коэффициенты, зависящие от физических параметров цепи; m, n - степени полиномов числителя и знаменателя, m £ n. Поэтому задача аппроксимации состоит в том, чтобы из всех функций класса (3) выбрать такие, квадрат модуля которых наилучшим образом приближается к единице в пределах полосы пропускания фильтра и к нулю вне ее характера, а точность аппроксимации зависит от критерия качества аппроксимации. Если по условиям задачи необходим монотонный характер аппроксимации, т.е. критерием качества аппроксимации служит ее монотонность, то наилучшей аппроксимирующей функцией будет та, которая обеспечивает наилучшую точность аппроксимации, т.е. наименьшее DçКç²инаибольшую крутизну АЧХ в переходной области. Из всех монотонных функций класса (3) одинакового с ней порядка n, наилучшей аппроксимирующей является та, которая при одинаковой точности аппроксимации имеет наименьший порядок, т.е. проще для реализации. Монотонную аппроксимацию осуществляют методом Тейлора. При этом наилучшими являются функции класса (3), квадрат модуля которых выражается через полиномы Баттерворта. Так аппроксимацию называют аппроксимацией по Баттерворту. Частотная характеристика фильтра Баттерворта в пределах полосы пропускания весьма близка к равномерной, и ее называют максимально плоской. Наклон переходного участка характеристики фильтра Баттерворта равен 6 дБ/октава на полюс. Таким образом, фильтр Баттерворта восьмого порядка будет иметь наклон переходного участка характеристики, равный 48 дБ/октава. Фильтр Баттерворта имеет нелинейную фазово-частотную характеристику; другими словами, время, которое требуется для прохождения сигнала через фильтр, зависит от частоты нелинейно. Поэтому ступенчатый сигнал или импульс, поданный на вход фильтра Баттерворта, вызывает выброс на его выходе. Используется фильтр Баттерворта в тех случаях, когда желательно иметь одинаковый коэффициент усиления для всех частот в полосе пропускания. На рис. 3 показана частотная характеристика фильтра Баттерворта нижних частот.

Иногда возможен немонотонный характер аппроксимации. Например, наилучшей из класса функций (3) одинакового порядка, обеспечивающих такую аппроксимацию, будет та функция, которая обеспечивает наилучшую точность (наименьшее DçКç²и наибольшую крутизну АЧХ в переходной области) или при одинаковой точности имеет наименьший порядок. Оптимальными в указанном смысле являются функции класса (3), квадрат модуля которых выражается через полиномы Чебышева. Такую аппроксимацию называют аппроксимацией по Чебышеву. По характеру аппроксимации она является разноволновой в полосе пропускания.

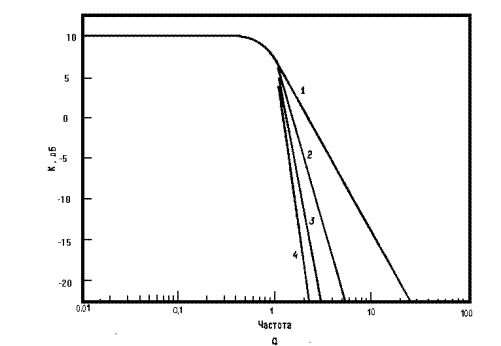
Рисунок 3. АЧХ фильтров Баттерворта нижних частот.

1-однополюсного (первого порядка); 2-двухполюсного (второго порядка); 3-трехполюсного (третьего порядка); 4-четырехполюсного (четвертого порядка);

На рисунке 4 представлены АЧХ фильтров нижних частот, аппроксимированных полиномами Чебышева. Если возможна немонотонность аппроксимации за пределами полосы пропускания, то используют дробную аппроксимацию. В этом случае квадрат модуля передаточной функции выражают через дробь. При этом коэффициент передачи на некоторых частотах полосы заграждения обращается в нуль. Эти частоты выбирают из условия обеспечения изоэкстремальности (равенства максимумов АЧХ в полосе задерживания) или равными частотам спектра сигнала, которые необходимо подавить.

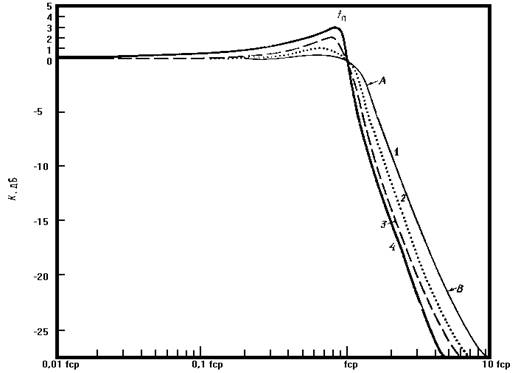
Рисунок 4. АЧХ фильтров Чебышева нижних частот.

1-второго порядка с неравномерностью в полосе пропускания 0,5 дБ; 2- второго порядка с неравномерностью в полосе пропускания 1 дБ 3- второго порядка с неравномерностью в полосе пропускания 2 дБ; 4- второго порядка с неравномерностью в полосе пропускания 3дБ; на участке А начальный наклон на переходном участке превышает  6 дБ/октава; на участке В скорость изменения ослабления приближается к 6 дБ/октава на один полюс.