Проектирование активных фильтров на операционных усилителях, страница 2

В зависимости от взаимного расположения полос пропускания и задерживания различают фильтры нижних частот (ФНЧ) (рис. 1,а), верхних частот (ФВЧ) (рис. 1,б), а также полосовые фильтры (ПФ) (рис. 1,в) и режекторные фильтры (РФ) (рис. 1,г).

а)                       б)                           в)                         г)

Рисунок 1. Идеализированные АЧХ различных типов фильтров

Для реальных АЧХ характерно непостоянство коэффициента передачи фильтра, как в полосе пропускания, так и в полосе задерживания. Кроме того, в реальных фильтрах невозможно получить скачкообразное изменение коэффициента передачи при переходе от полосы пропускания к полосе задерживания. В реальных АЧХ всегда существует полоса перехода, в которой коэффициент передачи фильтра непрерывно изменяется от значения минимально допустимого в полосе пропускания, до значения, максимально допустимого в полосе заграждения. Как правило, различие между этими значениями велико (сотни и тысячи раз). Поэтому для расчетов удобнее изображать частотные характеристики фильтра в виде зависимости от частоты коэффициента ослабления в логарифмическом масштабе (где К₀ - коэффициент усиления на частоте, по отношению к которой производят нормирование характеристики).

На рисунке 2, (а-г) приведены примеры реальных частотных характеристик ФНЧ, ФВЧ, ПФ и РФ соответственно.

Рисунок 2. Реальные АЧХ различных типов фильтров

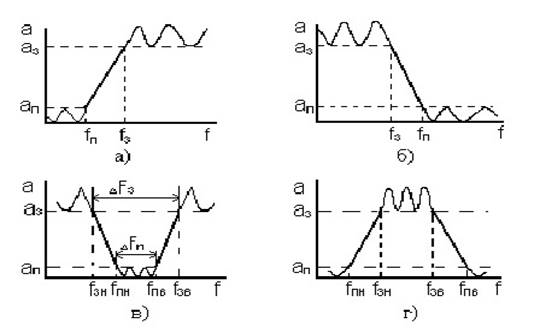Реальная характеристика помимо верхней или нижней граничной частоты полосы пропускания f_п характеризуется граничной частотой полосы задерживания f_з, максимально допустимым затуханием в полосе пропускания а_п и минимально допустимым затуханием в полосе задерживания а_з. Чем меньше отличаются граничные частоты f_п и f_з, и чем больше а_з, тем лучше фильтрующие свойства фильтра, т.е. его избирательность. Избирательность ПФ может характеризоваться также коэффициентом прямоугольности АЧХ

,                                           (1)

где DF_п - ширина полосы пропускания фильтра на уровне а_п, DF_з - ширина полосы пропускания фильтра на уровне а_з (рис. 2, в).

Средняя частота настройки ПФ и РФ (рис. 2, в-г):

.                                        (2)

2. Этапы проектирования активных фильтров

2.1. Аппроксимация амплитудно-частотных характеристик фильтров.

Первой задачей в процессе синтеза всякого фильтра является отыскание передаточной функции (в операторной или в комплексной форме), которая отвечает условиям практической реализуемости и одновременно обеспечивает получение необходимой АЧХ или ФЧХ (но не обеих) фильтра. Этот этап называется аппроксимацией характеристик фильтров. Таким образом, первой задачей синтеза является нахождение функции, с помощью которой можно построить фильтр, АЧХ которого должна удовлетворять условиям физической реализуемости и техническим требованиям, предъявляемым к устройству, также должна наилучшим образом приближаться к идеальной АЧХ, изображенной на рисунке 1. Процесс нахождения такой функции называют аппроксимацией. Характер аппроксимации зависит от выбора критерия качества аппроксимации.

Исходной функцией для решения задачи аппроксимации служит идеальная низкочастотная АЧХ (рис. 1а). Функция, аппроксимирующая эту характеристику, должна иметь квадрат модуля, близкий к единице в диапазоне частот пропускания , где W = f / f_п – нормированная (относительная) частота, и стремиться к нулю вне этого диапазона.

Любая физически реализуемая электрическая цепь имеет коэффициент передачи в виде аналитической дробно рациональной функции комплексной переменной

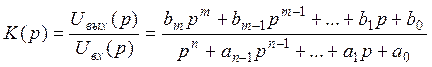,         (3)