Исследование заданной автоматической системы на устойчивость и результаты исследования. Проверка выполнения принципа суперпозиции в заданной автоматической системе

1.1. Заданная структурная схема автоматической системы с значениями параметров.

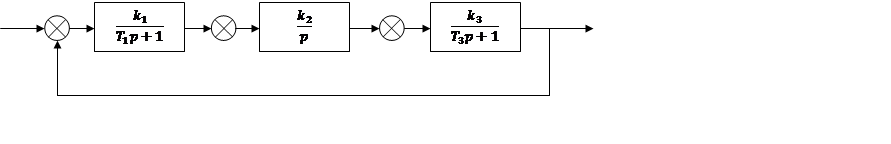g           x                                     f₁                                                           f₂                                     y

                      (-)

Параметры:

	2.75
	2.5
	1.6
	0.045
	0.1

1.2. Изложение процесса исследования заданной автоматической системы на устойчивость и результаты исследования.

Передаточная функция замкнутой автоматической системы имеет вид

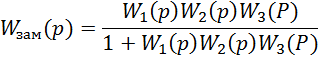
для нашей системы примет следующий вид

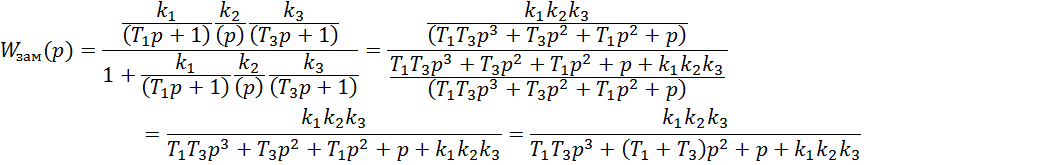
Используя замену

 получим

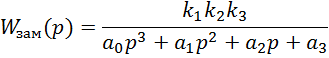
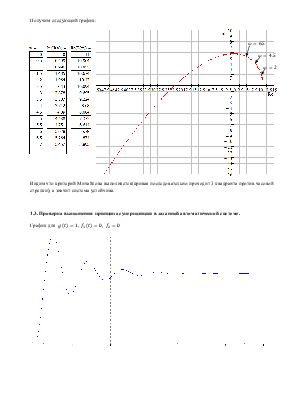
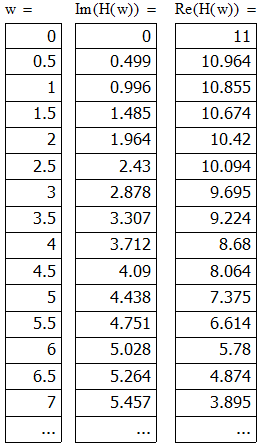
Исследуем систему на устойчивость с помощью критерия Михайлова

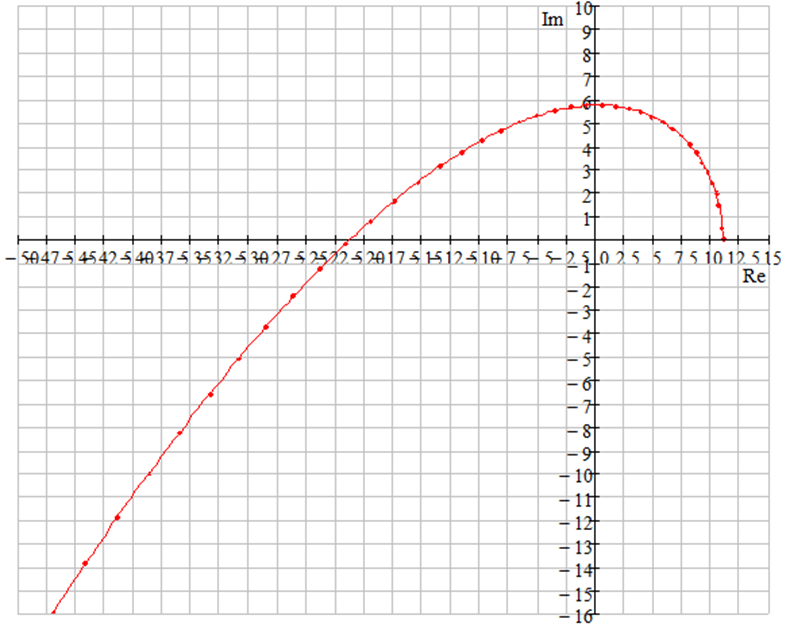Получим следующий график:

                                                                                                                                      

                                                                                             

                                                                                                                                                                                  

Видим что критерий Михайлова выполняется(кривая последовательно проходит 3 квадранта против часовой стрелки), а значит система устойчива.

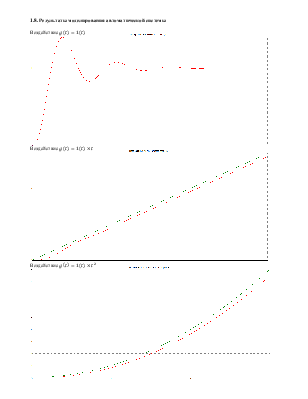
1.3. Проверка выполнения принципа суперпозиции в заданной автоматической системе.

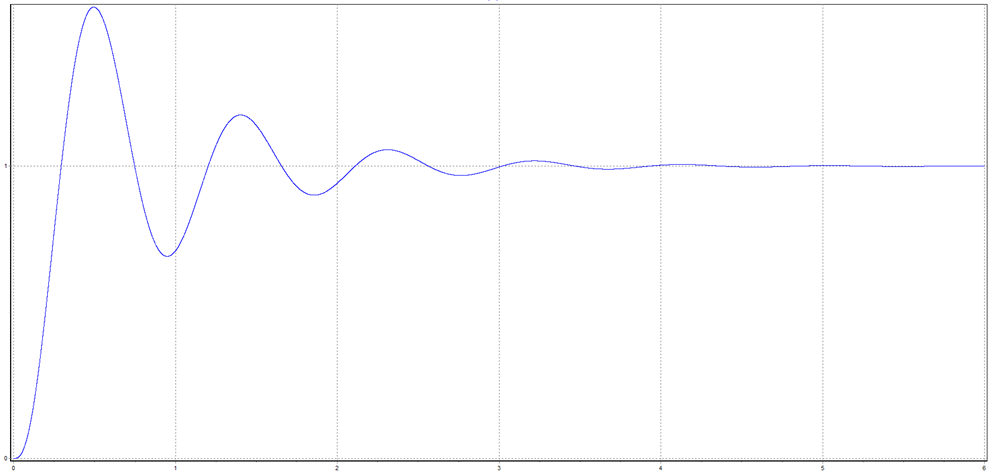
График для  

График для  

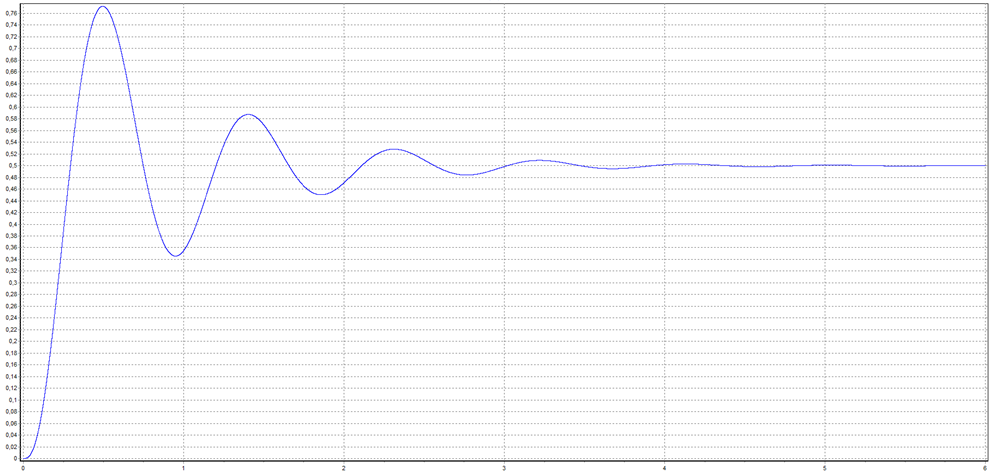
Из построенных выше графиков видим, что при изменении  с 1 на 0.5, значение коэффициента на графике изменилось в 2 раза, отсюда следует, что принцип суперпозиции выполняется.

1.4. Вычисление значения интегральной оценки качества аналитическим способом.

           

 

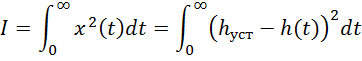
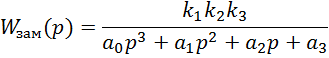
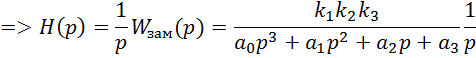
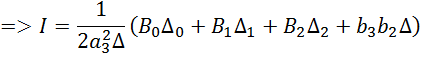
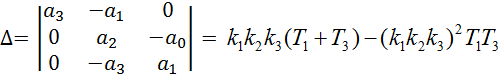
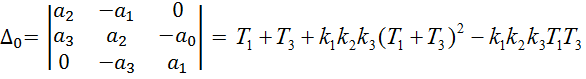
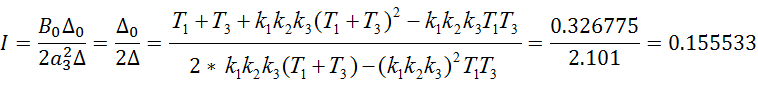
Интегральная оценка полученная при моделировании равна 1.55425, с долей погрешности равна оценке полученной аналитически.

1.5. Доказательство того, что система обладает астатизмом первого порядка, но не обладает астатизмом второго и третьего порядков.

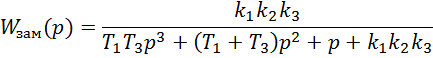
Разложение по ошибке в ряд по возрастанию степени р.

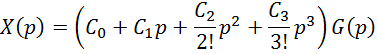
ряд сходится при   перейдем в область оригиналов

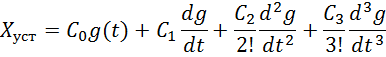
коэффициенты ошибок определяются по правилу разложения в ряд Тейлора.

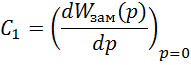
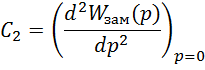
От коэффициентов зависит, обладает система астатизмом или нет

астатизм первого порядка

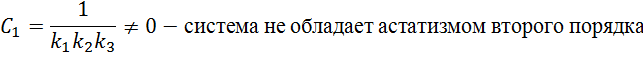
Т.к. система не обладает астатизмом второго порядка, значит не обладает и астатизмом третьего порядка.

1.6. Изложение процесса вычисления ошибки  и её значение при  и .

при :

при  :

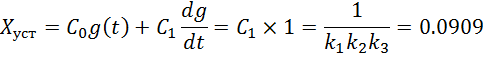
1.7. Доказательство того, что при  ошибка .

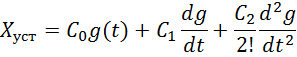
при :

Видим, что при коэффициенте  стоит , значит ошибка зависит от времени.

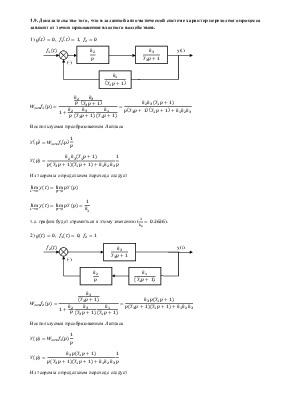
1.8. Результаты моделирования автоматической системы

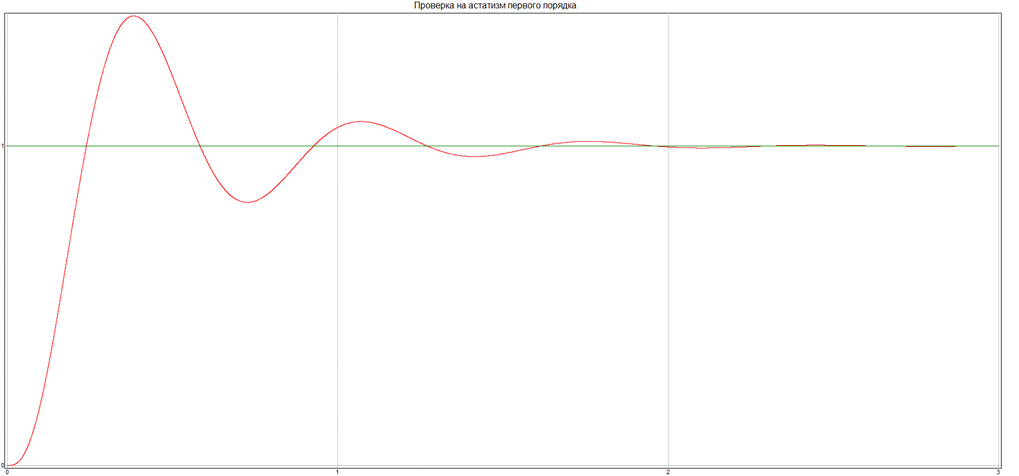Воздействие

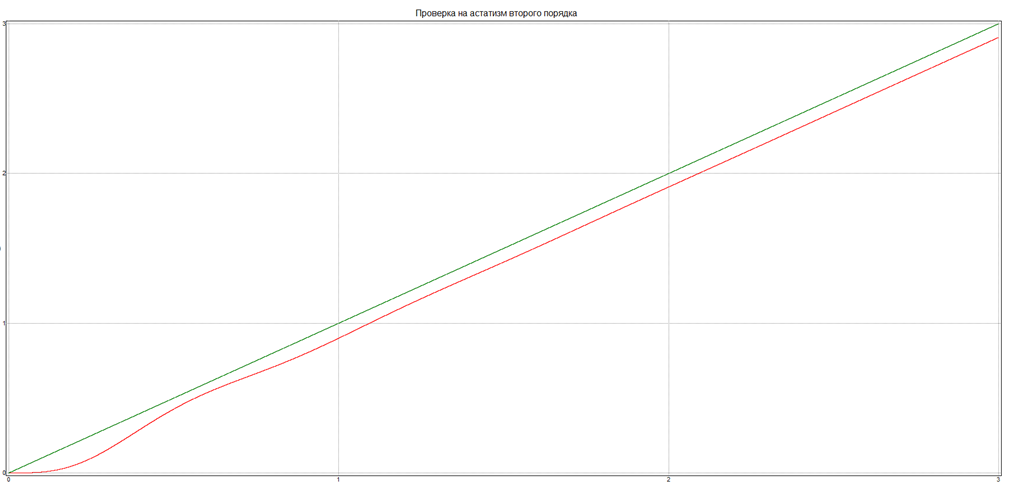Воздействие

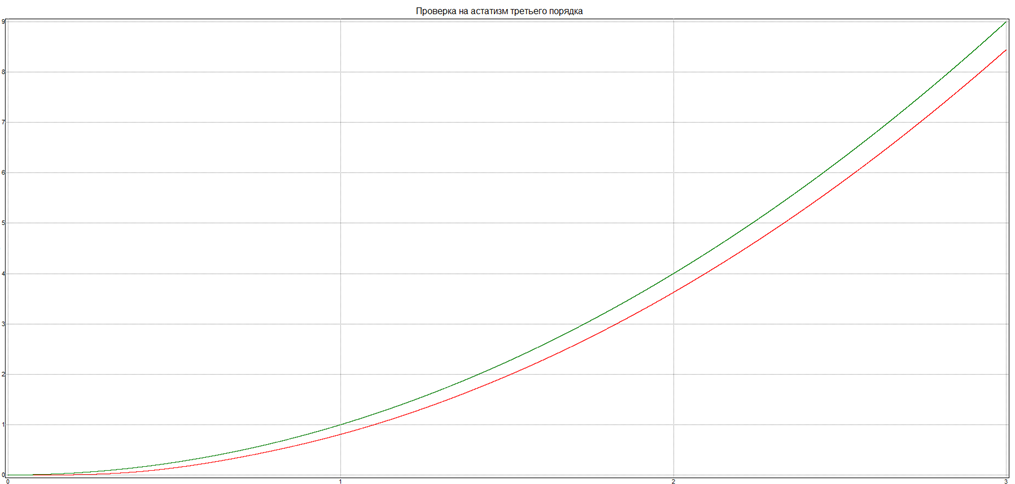Воздействие

1.9. Доказательство того, что в заданной автоматической системе характер переходного процесса зависит от точки приложения входного воздействия.

1)

                                                                                                        y(t)

                          (-)

 

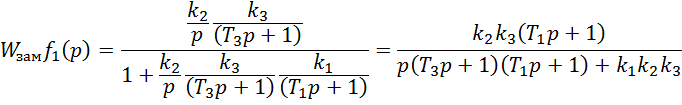
Воспользуемся преобразованием Лапласа

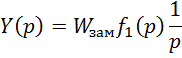
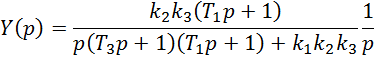
Из теоремы о предельном переходе следует

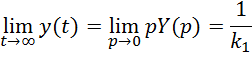
т.е. график будет стремиться к этому значению ().

2)

                                                                                                        y(t)

                          (-)

 

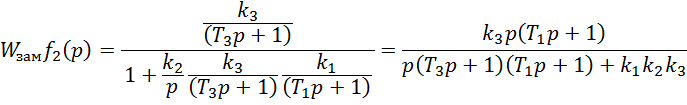
Воспользуемся преобразованием Лапласа

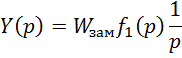
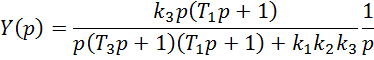
Из теоремы о предельном переходе следует

т.е. график будет стремиться к 0.

1.10. Моделирование подтверждающее доказательства предыдущего пункта.

1)

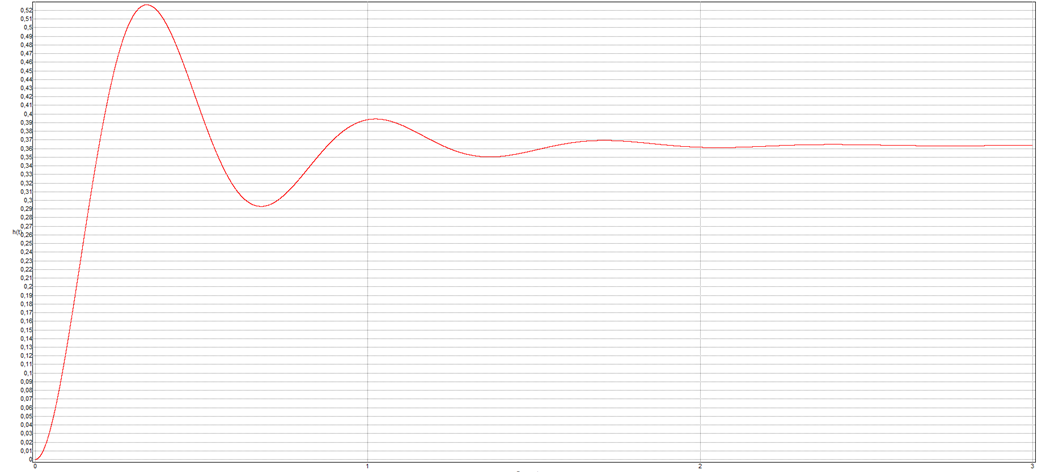
2)

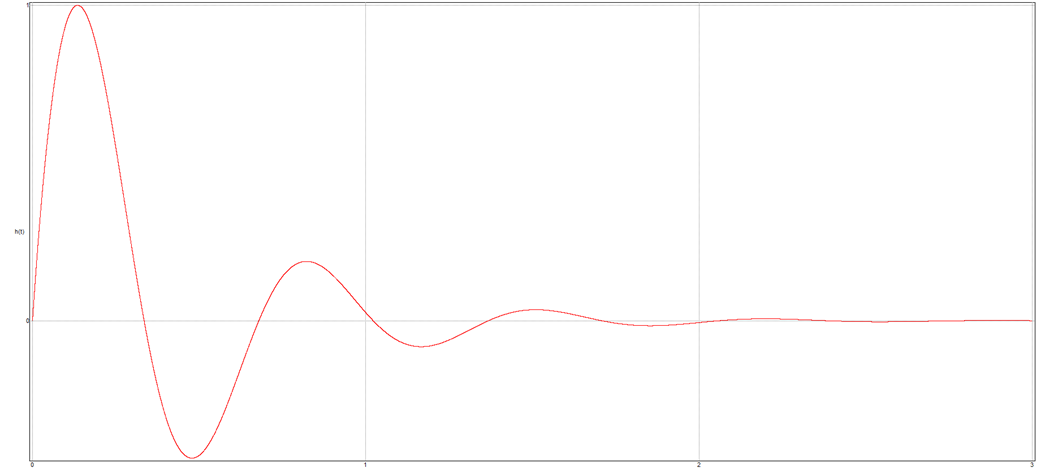
1.11. Получение зависимостей.

Статистическая погрешность равна

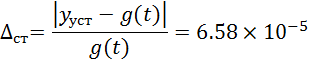
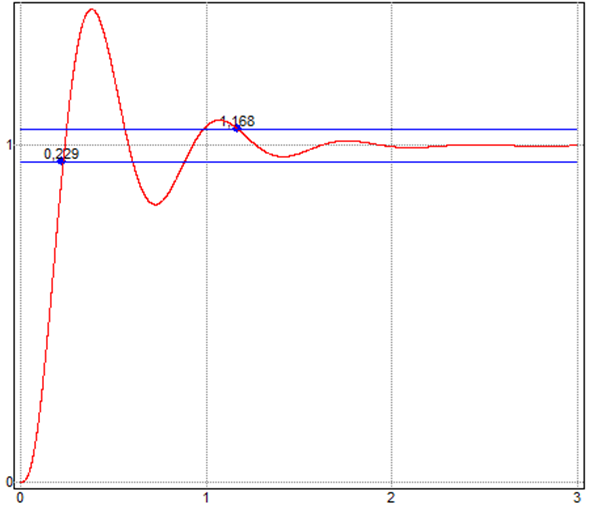
время регулирования

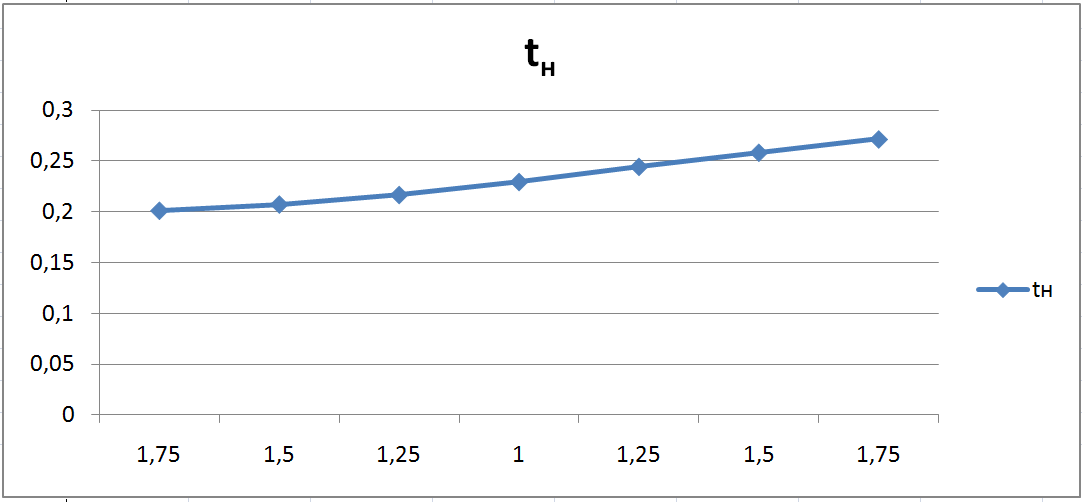
время нарастания

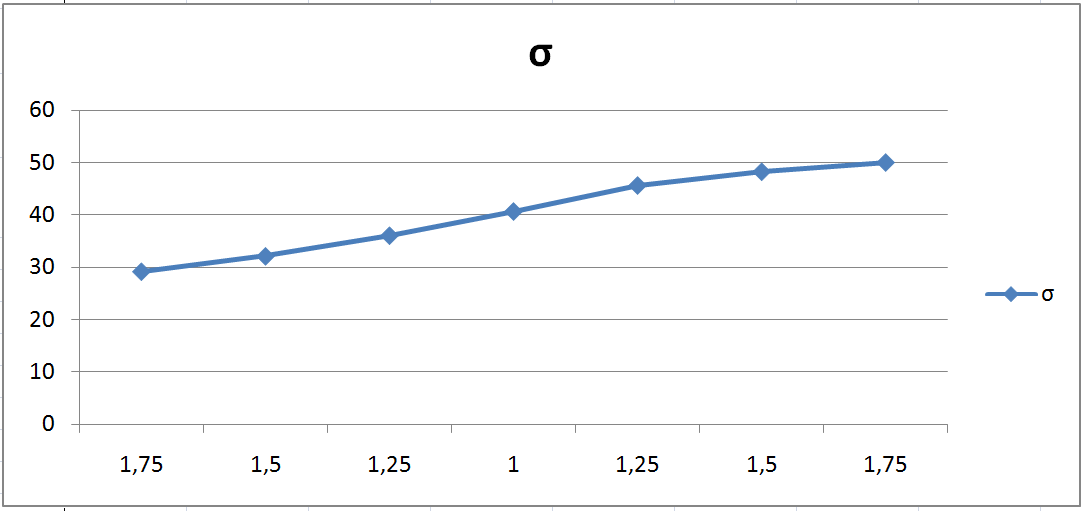
перерегулирование

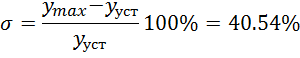
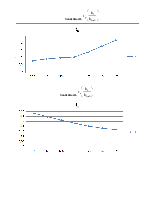
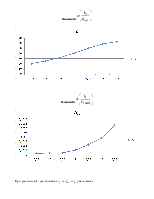
Зависимость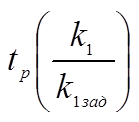

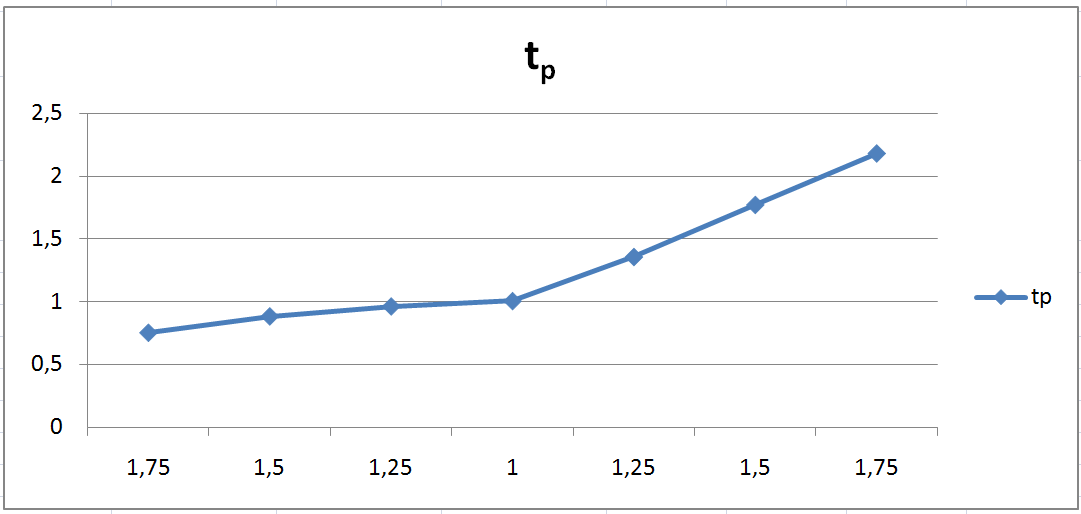
Зависимость

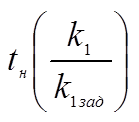
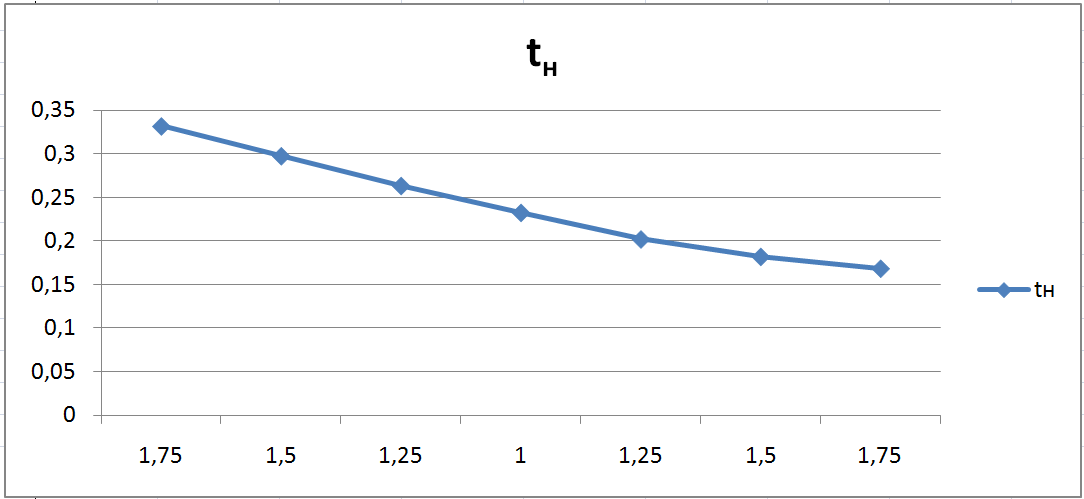
Зависимость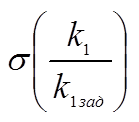

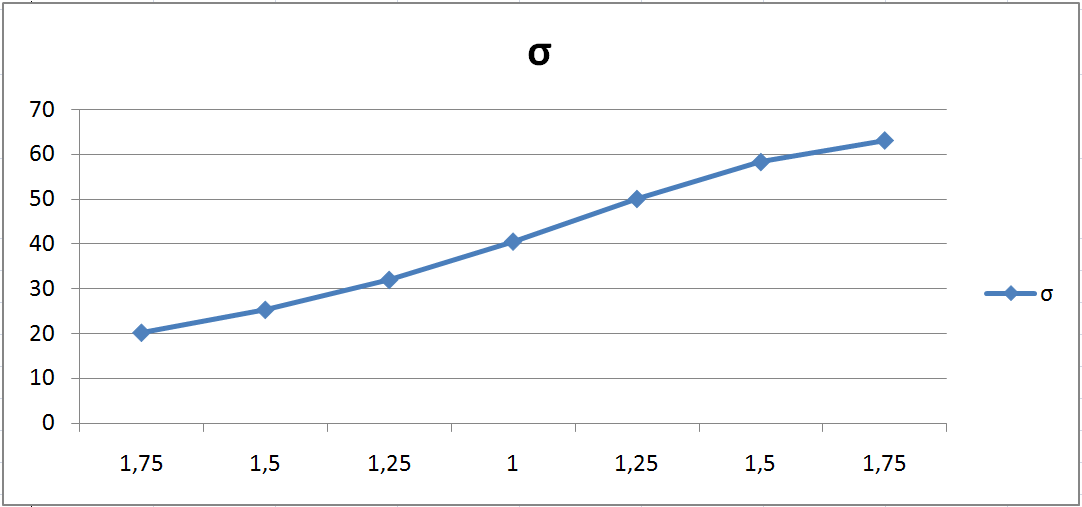
Зависимость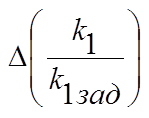

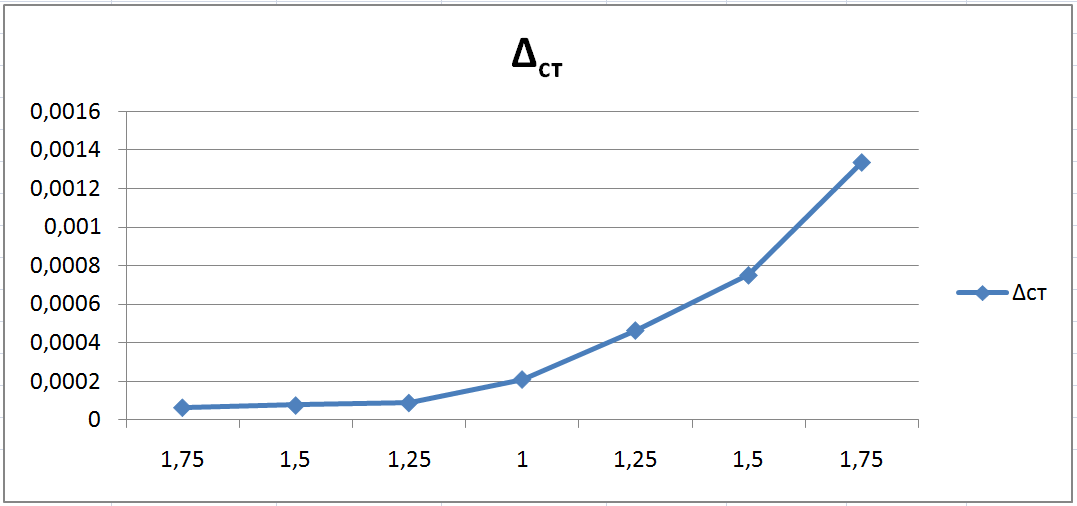
При  увеличении k₁ увеличивается t_p , s, Δ_ст , а t_н – уменьшается.

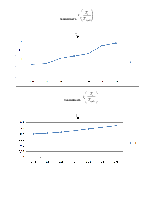
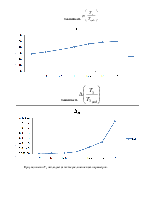
Зависимость

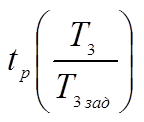
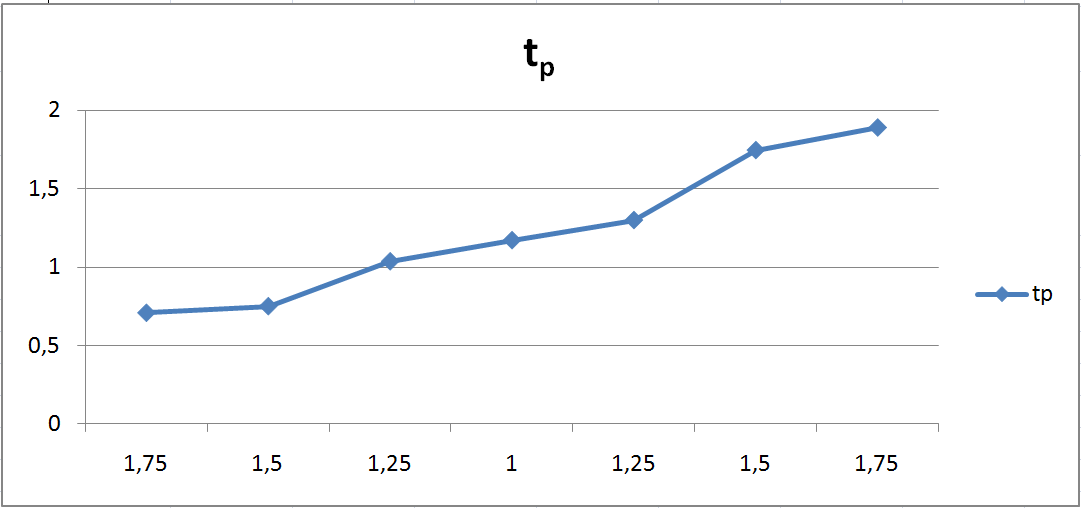
Зависимость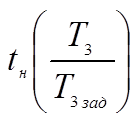

Зависимость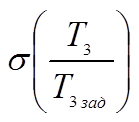

Зависимость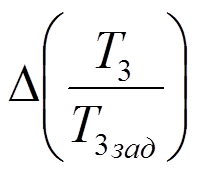

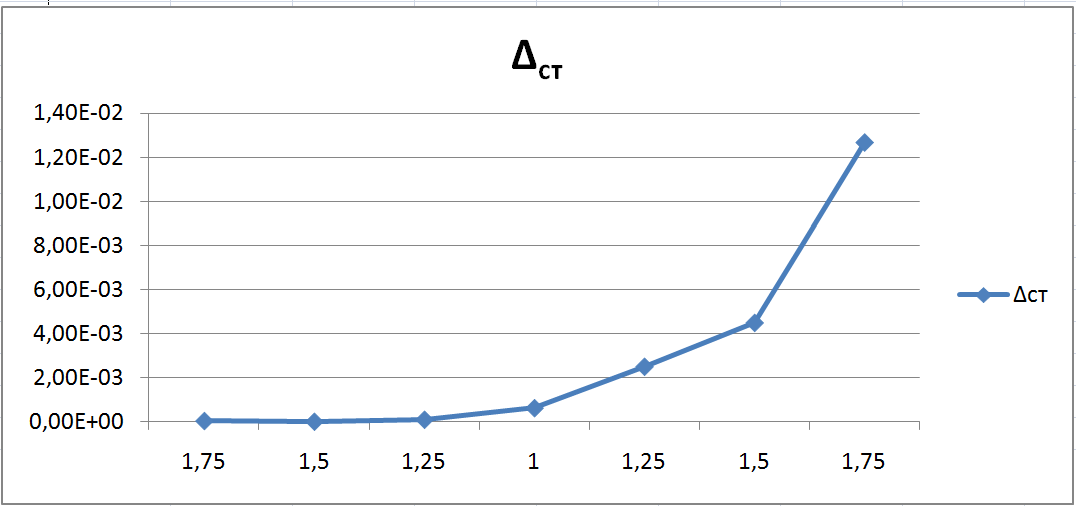
При увеличении Т₃ наблюдается также увеличение всех параметров .

Список использованной литературы:

1.  Куцый, А.С. Основы теории управления.  Лабораторный практикум: лабораторные работы № 1-5 / Н.Н. Куцый. – Иркутск: ИрГУПС, 2008. – 72 с.

2.  Теория систем автоматического регулирования / В. А. Бесекерский, Е. П. Попов. - Изд. 2-е , испр. и доп. - М. : Наука, 1972. - 767 с. : a-a-ил