Цель работы: Исследовать возможности модального метода синтеза цифровых регуляторов для линейных импульсных систем.
Дано:
Параметры |
||||
|
|
Желаемые корни |
|||
|
b0 |
a0 |
l1 |
l2 |
l3 |
|
2 |
1 |
0 |
0 |
0,5 |
Шаг дискретизации Т=0,1.
Решение.
1. Выполнить расчет дискретной передаточной функции по заданной непрерывной одним из известных методов.
Передаточная
функция непрерывной части системы имеет вид 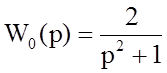 .
.
Найдем дискретную передаточную функцию с использованием z-преобразований.
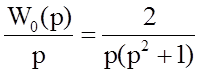
Разобьем исходную передаточную функцию на элементарные дроби.
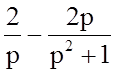
Запишем
соответствующие z-преобразования
для каждой дроби и их сумму умножим на 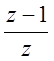 .
Имеем
.
Имеем
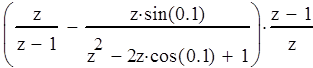
После упрощения получим следующий вид дискретной передаточной функции с фиксатором нулевого порядка
![]()
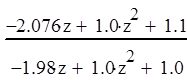
2. Для объекта, математическая модель которого задана дискретной передаточной функцией:
![]()
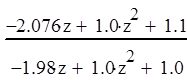
выполнить синтез астатического регулятора модальным
методом по формулам 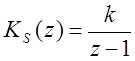 ,
,
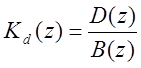 , где
, где ![]() .
Желаемые корни соответствуют минимальной длительности процессов в замкнутой
системе
.
Желаемые корни соответствуют минимальной длительности процессов в замкнутой
системе
Для определения коэффициентов k, d1, d0 приравниваются выражения:
![]()
и
![]() .
.
Имеем:
![]()
В результате расчетов по заданным корням l1=0 l2=0 l3=0.5, что соответствует минимальной длительности процессов в замкнутой системе, получена следующая система уравнений:
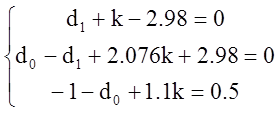
Решая данную систему, имеем следующие значения искомых
коэффициентов: ![]()
Тогда выражения корректора статики и динамики
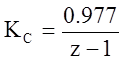
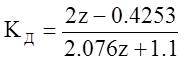
3. На рисунке 1 изображена замкнутая дискретная система без регулятора и с регулятором. Переходные процессы обоих представлены на рисунке 2. Также на рисунке 1 представлена структурную схему регулятора на звеньях задержки. Переходный процесс последней совпадает с моделью регулятора в общем виде, что подтверждает правильность построения модели на звеньях задержки.
4. На основании полученных результатов, можно сделать вывод, что достигнута минимальная длительность переходного процесса. Время регулирования системы уменьшилось с 3 до 1 секунды. Кроме того, изменился коэффициент усиления сигнала (установившееся значение выросло с 0,35 до 1).
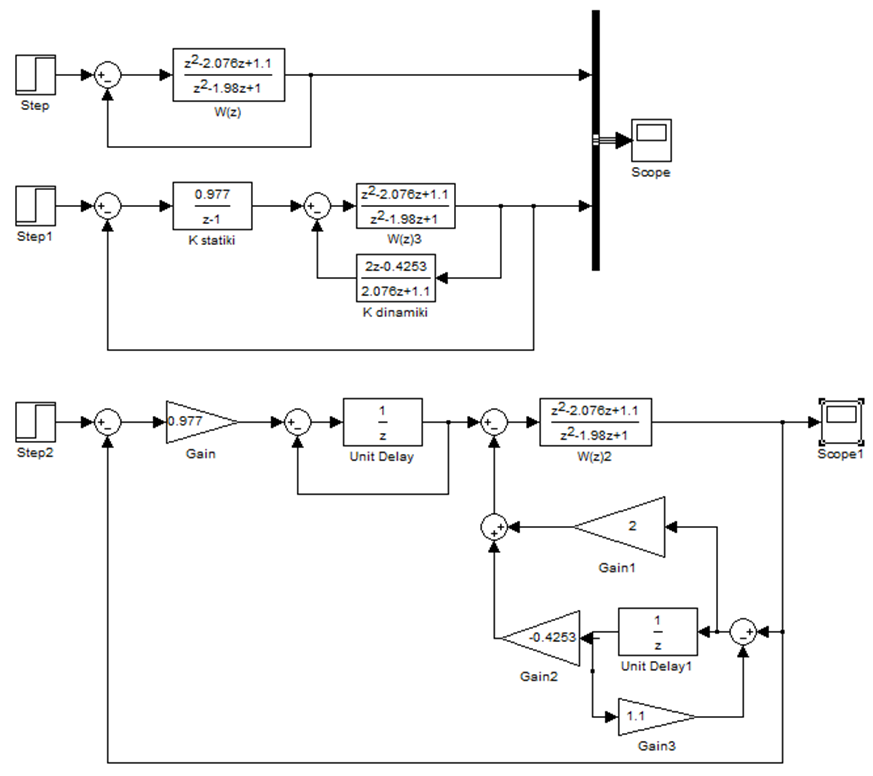
Рисунок 1 – Модели дискретных систем без регулятора, с регулятором в общем виде и на звеньях задержки.
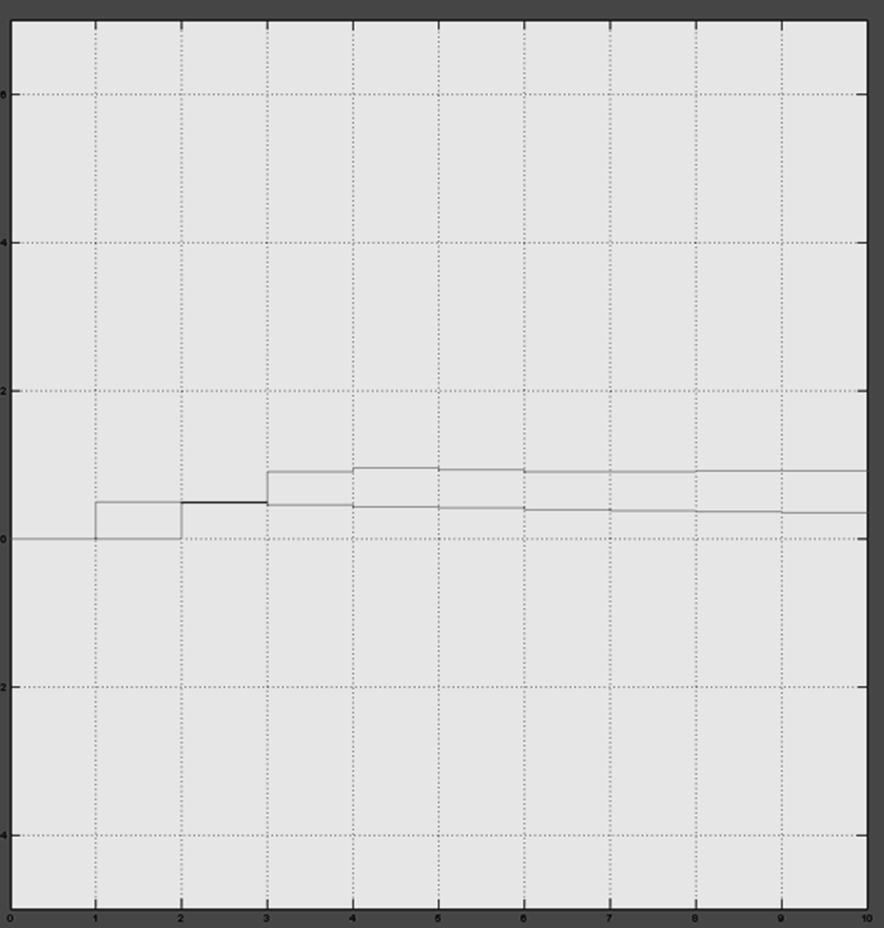
Рисунок 2 – Переходные процессы в системе без регулятора и с ним.
Вывод: Исследовали возможности модального метода синтеза цифровых регуляторов для линейных импульсных систем.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.