В качестве первой цели поставим задачу вычисления фонда страховых возмещений, который с надежностью γ =99% обеспечит все поступающие требования о выплате возмещений по данной совокупности договоров. Страховая компания исходит из того, что величина резерва страховых выплат должна быть такой, чтобы общие выплаты ее не превышали. Это условие можно записать формально как:
![]()
где U- величина резерва страховых выплат.
![]()
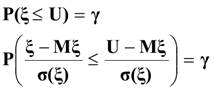
Обозначим как α (γ) правую часть неравенства, стоящего под знаком вероятности:
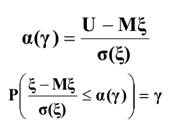
Согласно центральной предельной теореме, если ξ j – ограничены и одинаково распределены, то при больших значениях n:
![]()
- функция распределения вероятностей нормальной случайной величины.
По таблице значений распределения нормальной случайнойвеличины находим, что
α(99%) = 2,33. Следовательно, величина страхового резерва может быть рассчитана как:

Страховая компания со всех клиентов данной совокупности должна собрать U. Следовательно, если сложить все премии, слева получим U, а справа:
![]()
где как Lобщ. мы обозначим фонд суммарной страховой надбавки.
Отсюда получим что:
![]()
Остается задача разделения фонда суммарной страховой надбавки между различными договорами. Существуют различные способы и подходы к решению этой задачи. Здесь мы приведем наиболее часто используемые, отличающиеся подходами к учету интереса страхователя.
IСПОСОБ заключается в том, что страховая надбавка пропорциональна индивидуальным средним выплатам, т.е.:
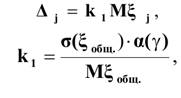
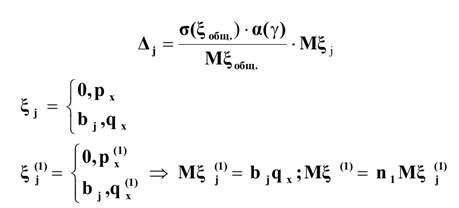
Аналогичным образом определяются риски остальных частей совокупности:
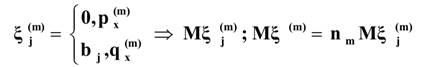
nm- ожидаемое количество договоров в доле m-ом субпортфеле
![]()
- суммарное среднее ожидаемое значение страховых выплат.
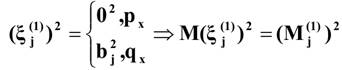
Аналогичным образом определяется дисперсия для отдельных частей совокупности:
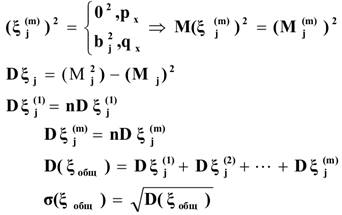
σ- общее среднеквадратическое отклонение,
γ- уровень выполнения обязательств по выплатам страховой компанией. Каждая страховая компания определяет для себя различный уровень надежности выполнения обязательств (который, однако, должен быть не ниже регламентируемого Страхнадзором). Если уровень надежности равен, например, 99%, то получим:
α(99%) = 2,33.
Здесь, согласно закону больших чисел, использована нормальная аппроксимация, и соответствующее табличное значение.
II. СПОСОБ заключается в том, что страховая надбавка устанавливается пропорционально индивидуальной дисперсии выплат, т.е.:
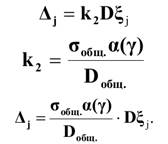
Недостатком этого способа является несоответствие единиц измерения: страховая надбавка измеряется в единицах дисперсии, т.е. в руб2. (Это учитывается в размерности коэффициента k).
III.СПОСОБ заключается в том, что страховая надбавка пропорциональна среднеквадратическому отклонению, т.е.:
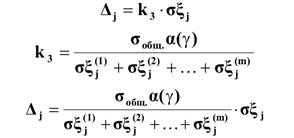
Этот способ используется наиболее часто.
Заключение
Из вышеизложенного можно сделать следующие выводы: вероятность разорения страховщика, можно получить, применяя функцию распределения случайной величины. Так же, использовав математическое ожидание этой функции, определим суммарную рисковую премию. Что же касается степени риска – была выведена формула, включающая в себя, как мат. ожидание, так и дисперсию. Эти данные, в практике, могут заметно облегчить проблему страховой компании в определении оптимальных тарифов, но, заметим, не гарантируют достоверных результатов. Так как в конечном итоге, все опирается на вероятность наступления страхового случая, который, в свою очередь является непредсказуемым.
Список используемых источников:
1. Корнилов И.А. – Элементы страховой математики. 2003 г.
2. Статья: Мат статистика. URL: 2013 г.
3. Фалин Г.И – Актуарная математика в задачах. 2003 г.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.