Использование функции распределения ущерба при оценке вероятности разорения страховщика, страница 6

и  указана  корректировка  представлений  по  мере поступления новой информации:

Дальнейшее  развитие  этого  направления  и  применение  этого аппарата  для  решения  более  сложных  актуарных  задач  достаточно подробно изложено в кн. Карри/6/ .

6.  Некоторые проблемы определения рисковой надбавки.

При  исследовании  портфеля  долгосрочных  договоров  также возникает задача оценки вероятности разорения. Здесь анализируется поток  заявок (исков). В  результате  получается  формула,  аналогичная формуле  для  краткосрочной  модели.  Это  позволяет  указать  правила расчета рисковой премии и рисковой надбавки в зависимости от объема собственных  средств.  Разумеется,  в  долгосрочном  страховании повышается  роль  задачи  определения  коэффициента  рассрочки  при переходе от единовременной премии к периодической.

Кроме  того,  здесь  не  учитывается  время  фактического предъявления  требования  о  выплате.  Рассматривается  фиксированная совокупность договоров, по которым в момент времени t=0 поступают  премии, формирующие резерв страховых выплат, который к моменту t=1 должен обеспечить все выплаты с некоторым достаточно высоким уровнем надежности.

Рассмотрим договор с фиксированным ущербом (смерть, кража, угон автомобиля), в котором человек  платит  страховой  компании“п” (руб.) -  страховую  премию. Компания соглашается выплатить сумму b(руб.), если страховой случай произойдет в течение года. Иначе страховая компания ничего не платит.

Известно, что b больше «п». Купив за“п” (руб.) страховой полис,  застрахованный  избавил  свою  семью  от  риска  финансовых  потерь, связанных  с  неопределенностью  момента  наступления  страхового случая  и  величиной  потерь.  Этот  риск  приняла  на  себя  страховая компания. Если страхового случая нет, то иск к страховой компании равен нулю. Иначе иск к страховой компании составит b(руб.). Для упрощения  расчетов  положим  b=1 - единица  денежной  суммы. (В страховании принят термин «единица страховой суммы».)  

Этот индивидуальный риск является элементарной составляющей финансового  риска  страховой  компании.  Случайную  величину,  определяющую данный элементарный риск, обозначим, как ξ_j. Индекс j означает, что данная случайная величина описывает выплаты на одного (скажем,  с  номером  j) клиента.  Вероятность  наступления  страхового случая  может  зависеть  от  некоторых  факторов (при  страховании автомобиля от угона– от марки и возраста автомобиля, а также, от его состояния). При страховании жизни вероятность зависит, прежде всего,  от  возраста  застрахованного.  В  дальнейшем,  для  определенности, рассматриваем именно такой договор(на случай смерти).

Распределение ζ _j имеет следующий вид:

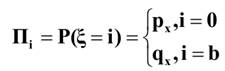
x- возраст застрахованного,

p_x- вероятность того, что человек в возрасте x лет проживет еще по меньшей мере один год,

q_x- вероятность того, что человек в возрасте x лет умрет в течении ближайшего года.

Рисковая  премия  обеспечивает  выполнение  принципа эквивалентности  финансовых  обязательств страховщика  и страхователя,  состоящего  в  том,  что,  в  среднем,  и  страхователь,  и страховщик  должны  платить  одинаково.  Следовательно,  рисковая премия одного договора должна быть равна математическому ожиданию величины индивидуального иска:

Страховая (рисковая) надбавка еще называется платой за риск и должна  отражать  возможные  флуктуации(колебания,  отклонения)  индивидуального иска. Так как риск перераспределяется между многими участниками  страховой  совокупности,  то  страховая  надбавка определяется для всей совокупности договоров.

Понятно, что чем больше совокупность одинаковых независимых рисков, тем меньше фактический суммарный риск отличается от своего математического  ожидания.  В  качестве  критерия  оценки  суммарного риска  в  страховании  используется «степень  риска» - коэффициент вариации суммарных выплат по данной страховой совокупности.