Подход, основанный на ковариации, имеет практическое применение при страховании(и перестраховании) крупных промышленных рисков. В этих договорах подобный контроль(проверка, не содержатся ли в ранее сформированном портфеле элементы нового риска) имеет решающее значение. И размер премии существенно повышается с ростом страховых сумм.
Иногда строят конструкцию надбавки, опираясь на так называемую производящую функцию, для которой очень удобно использовать логарифм:
![]()
но не ![]()
Иногда возможен вариант, основанный на принципе максимального возможного возмещения риска:
![]()
Замечание: в этой формуле необходимо предполагать конечность MAX(Z), в противном случае P= ∞, то есть риск нестрахуем.
Ранее отмечено, что на практике часто нагрузку конструируют:
![]()
В теоретическом плане весьма интересен подход, основанный на функции полезности.
4. Сравнение различных договоров с помощью функции
полезности
Пример2. Пусть функция полезности имеет вид:
U(x) = x 2/3, x>0.
Ущерб X равномерно распределен на(0;100). Есть возможность застраховать риск в трех компаниях на следующих условиях: а) полная страховая защита за взнос 52; в) защита с безусловной франшизой в 10, (при взносе 42), т.е. выплата равна 0, если X<10, и равна X-10, если X>10;
c) частичная защита(при взносе 45): выплата X, если X<50, и выплата (50 + (X-50)/2), при X>50.
Возможен и отказ от страхования. Владелец располагает капиталом в 150. Какой вариант ему предпочесть?
Решение. Сначала заметим, что если убытков не будет, то
U(150 - 0) = U(150) = 1502/3= 28.23
Если убытки максимальны, то
U(150 - 100) = U(50) = 502/3= 13.57
Таким образом, получены данные для построения шкалы. Сравним варианты.
1) Отказ от страхования. Ожидаемая полезность:
![]()
2) Страховаться в компанииA. Капитал к концу срока:
150-52 = 98, а его полезность: U(98) = 982/3= 21.26
3) Страховаться в компании B. Капитал: (150-42-X) приX<10, или(150-42-10) при X>10, тогда его полезность:
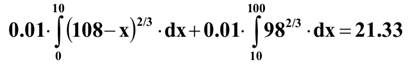
4) Страховаться в компании C.
Капитал: 105, при X<50; либо (150-45-X+(50+(X-50)/2)) = 130 - 0.5⋅X, при X>50.
Тогда полезность:
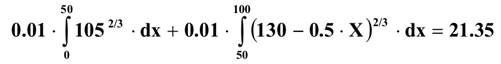
Теперь сравниваем результаты и выбираем max функции полезности. Очень маленькое преимущество у компании С при всей парадоксальности предложенных ей условий и предварительных наших представлений.
Рассмотрим еще некоторые примеры. Пусть имущество не подвергнется ущербу с вероятностью 0.75. Ущерб, если он будет, распределен экспоненциально со средним, равным 100. Тогда ожидаемые убытки составят 25. В данном случае используется условное математическое ожидание.
Для дальнейших исследований необходимо построить функцию полезности. В частности, можно показать (см. Карри/6/), что если клиент использует функцию:
![]()
То при полной защите ему придется согласиться заплатить 44.63 (при средних убытках 25, он переплатит 19.63). А если договор предусматривает возмещение лишь половины ущерба(то есть в среднем не 25, а 12.5), то клиент заплатит 28.62(больше на 16.12).
5. Понятие о доверительных оценках в страховании
В страховой компании часто возникает ситуация, при которой конкретный клиент в течение длительного времени периодически продлевает свой страховой договор(например, страхование дома). Компания накапливает информацию о нем за это время. Поэтому к данному клиенту может быть применен как подход, общий для всех клиентов из некоторой однородной группы, так и индивидуальный, основанный на его специфике. Следовательно, у компании есть два источника информации об этом клиенте.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.