Задачи оптимизации. Определение оптимального управления

Лекция №5

ЗАДАЧИ ОПТИМИЗАЦИИ

Определение оптимального управления состоит в выборе таких управляющих воздействий, при которых критерий качества принимал бы в зависимости от его смысла максимальное или минимальное значение и включает в себя три задачи:

выбор и математическое описание цели оптимального управления в виде соответствующих критериев оптимальности;

определение математической модели объекта и установление ограничений на векторы Y, X и u, а также оценку свойств объекта и влияния возмущений f(t);

выбор метода синтеза оптимального управления .

Принято различать статический (установившийся) и динамический режимы работы объекта. Соответствующие уравнения математических моделей используют при формулировке задач оптимизации.

Процессы, протекающие в объектах общего типа, полностью определяются математической моделью в виде системы нелинейных дифференциальных уравнений состояния и выхода, например, вида

,              (1.24)

где f(...) и j(...) – матрицы-столбцы, состоящие из n и m элементов соответственно.

Часто эта модель для упрощения задачи при удовлетворительной точности результатов может быть сведена к линейной, представленной в виде линейных уравнений состояния и выхода:

,     (1.25)

где А, В, В_f, С, D – матрицы коэффициентов, размерность которых зависит от размерности векторов X, u, Y и f_в(t).

В статических режимах работы стационарных объектов компоненты векторов управления U при отсутствии или постоянных возмущениях f_в(t) неизменны во времени, а значения составляющих вектора выхода Y определяются статическими характеристиками объекта. Для нестационарных объектов координаты объекта и его характеристики изменяются во времени. В случае квазистационарных объектов можно рассматривать квазистатические режимы на отдельных интервалах времени [t_i, t_i + T_i], где i=1, 2, ..., k;  k = (t_к – t₀)/N; N – число интервалов квазистационарности.

Задачи оптимизации по скалярным критериям. Оптимизацию по скалярным критериям производят как для статических, так и для динамических критериев.

1. При оптимизации статических и квазистатических режимов скалярный критерий качества может быть нелинейным и линейным соответственно:

;                                (1.31)

,                            (1.32)

где C₀(t) – коэффициент, изменяющийся во времени из-за влияния неконтролируемых возмущений f_в(t) для нестационарных объектов; С_u и C_z – матрицы-строки постоянных коэффициентов.

Оптимальное управление объектом в квазистатических или статических режимах состоит в определении таких векторов U°(T_i) или U°, которые удовлетворяли бы условиям (1.26), если объект нелинейный, и условиям (1.28) или (1.29), если объект линейный, а также доставляли минимум или максимум критерию качества, заданному в виде (1.31) или (1.32). При этом на компоненты вектора управления накладываются ограничения U° Î Wu. Эти ограничения могут быть различными. Наиболее распространенными типами ограничений являются двусторонние ограничения U_min £ U £ U_max. При U_min = 0 и U_max = ¥ ограничения имеют вид U ³ 0 (неотрицательность переменных).

2. При оптимизации динамических режимов объекта по скалярным критериям уравнения состояния нелинейного нестационарного объекта могут быть записаны в неявном виде:

.              (1.36)

Применяя скалярные критерии оптимальности динамических режимов, задачи оптимального управления нестацио­нарным объектом в динамике для детерминированного и стохастиче­ского объектов запишем в виде

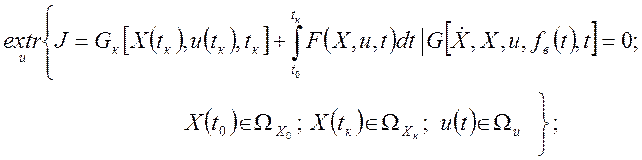          (1.37a)

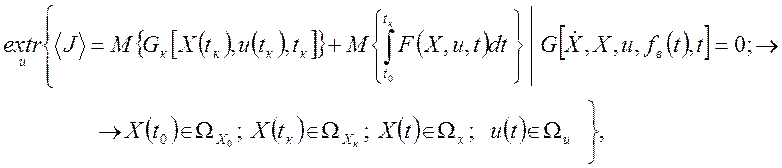          (1.37б)

где условия  означают, что начальное и конечное значения векторов состояния заданы и принадлежат множествам .

В экстремальных задачах (1.37а) и (1.37б), кроме ограничений фазовых координат и управлений, имеются функциональные ограничения, заданные в виде уравнений G(...) = 0 – математических моделей динамики объектов (1.36), являющихся дополнительными условиями при отыскании min (или max) критериев J или <J>.

Задачи оптимизации по векторным критериям. Для сложных технологических процессов и объектов, представляющих собой «большие» системы, задача оптимизации формулируется по векторному критерию оптимальности (см.§1.2). Такие задачи называют многокритериальными или задачами векторной оптимизации.

При векторном критерии оптимальности

J =Q(Y, U, Z, T_i)                                   (1.38)

задача оптимизации квазистатических режимов может быть сформулирована, подобно (1.33), как векторная задача нелинейного программирования общего типа:

,   (1.39)

где Q(...) – вектор-столбец l функций частных критериев.

Задача (1.39) вырождается в задачу линейного программирования, если все частные критерии и уравнения объекта являются линейными.

При решении задачи (1.39) необходимо так выбрать вектор управлений U(Т_i), чтобы каждому частному критерию J_j обеспечить минимум (или максимум). Для стационарных объектов вектор U⁰ не зависит от времени.