Дифференциальные уравнения и передаточные функции линейных непрерывных систем автоматического регулирования

Лекция 2

(6 часов)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ

Математический аппарат при анализе непрерывных САР.

Понятие оператора

Простейшим математическим понятием является число, выражающее количественно величину параметра либо воздействия.

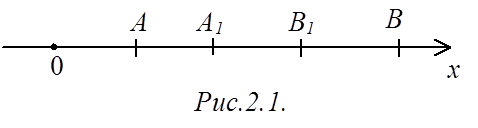Более широким понятием является числовая ось, на которой расположено бесконечное множество чисел (рис.2.1). На отрезках AB и A₁B₁ также расположено бесконечное число точек. В таких случаях говорят, что множество AB шире множества A₁B₁. Сами эти множества, закон пересчета чисел которых неизвестен, называют континуальными. Когда удается указать закон пересчета чисел, множество называют счетным. Если все точки множества можно пересчитать, то множество называют конечным.

На практике инженерам приходится иметь дело именно с континуальными множествами чисел, которые могут отражать диапазон изменения некоторого воздействия (управляющего или возмущающего) или какого-либо параметра.

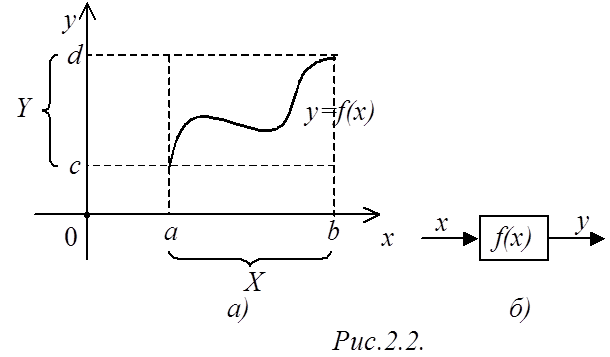Уточним понятие функции. Функцией называется всякое соответствие между точками одного множества и точками другого множества (каждой точке одного множества соответствует точка другого множества). Например (рис.2.2а), если заданы множества чисел  и , и функция , то в этом случае говорят, что функция f определена (задана) на множестве U со значениями на множестве X.

Функция в инженерном сознании ассоциируется с безынерционными звеньями (рис.2.2б), реализующими требуемую функциональную зависимость.

Функционалом называется всякое соответствие между функциями одного множества и точками другого множества (каждой функции соответствует точка). Функционалы задаются на множестве функций. Типичный пример функционала:

          ,

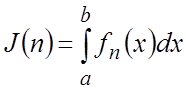где f(x) – некоторая заданная функция;  – варьируемое количество элементарных участков интегрирования.

Другой пример – если известна функция двух переменных , то можно построить функционалы типа

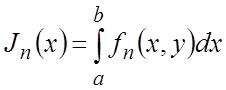
при разных значениях аргумента x и фиксированном .

В ТАУ функционалы используются при построении оптимальных САУ для определения требуемого соотношения между параметрами САР.

Всякое соответствие между функциями одного множества (X) и функциями другого множества (Y) называется оператором. Например (рис.2.3а), пусть A – оператор, отражающий коэффициент передачи (усиления) некоторого устройства (). Тогда оператор A связывает все входные функции x(t) с выходными y(t), воздействуя на входной сигнал (в нашем примере – умножая его в каждый момент времени на коэффициент k – усиливая его). Такое звено в результате формирует выходную функцию y(t), отличающуюся от входной x(t) на постоянный множитель (рис.2.3б).

Понятие оператора широко используется в ТАУ. Наиболее широко используемыми являются операторы дифференцирования и интегрирования (определения неопределенного интеграла).

В частности, если оператор

          A=TD,

где 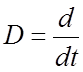 – символ (оператор) дифференцирования по времени, T – некоторая постоянная времени [c], то воздействие оператора на некоторую входную функцию x(t) дает выходную функцию

                    .

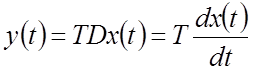То есть, результатом использования оператора TD есть то, что он, воздействуя на входной сигнал x(t), выдает производную от этого сигнала по времени в каждый момент t, помноженную на коэффициент T (рис.2.4).

Обратный оператор 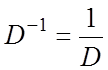 соответствует интегрированию. Например, если

          ,

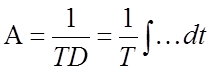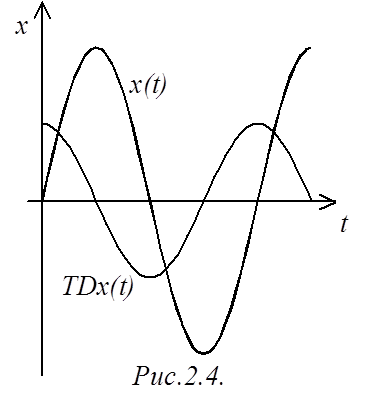то выходной сигнал

                    .

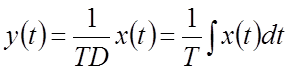Результатом использования оператора интегрирования есть то, что он, воздействуя на входной сигнал x(t), выдает для каждого нового значения t, новое значение площади. Геометрический смысл оператора интегрирования понятен из рис.2.4.

Таким образом, если оператор дифференцирования "проникает" внутрь сигнала, в его отдельные точки, то оператор интегрирования выдает самые обобщенные представления о входном сигнале.

Более сложными операторами, используемыми в ТАУ, являются операторы-полиномы (многочлены) вида

          .

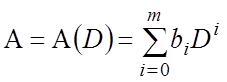Их называют еще дифференциальными операторами. Смысл такого оператора в том, что входной сигнал преобразуется в выходной вида:

              .

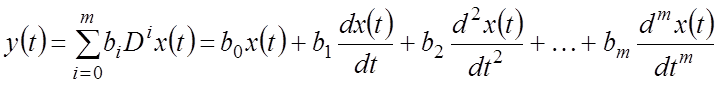Полезность этой записи в том, что дифференциальные уравнения высокого порядка можно записать в краткой операторной форме.

Самыми сложными операторами, используемыми в ТАУ, являются операторы, представляющие собой отношение операторов-полиномов:

,

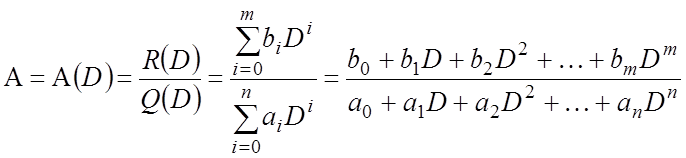причем  – это ограничение накладывается условиями физической реализуемости.

Смысл любой операторной записи вида

          ,

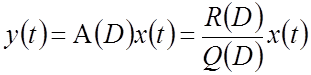заключается в том, что ей соответствует дифференциальное уравнение, связывающее вход x(t) с выходом y(t) (рис.2.3а):

                    .

При этом оператор  при входной переменной  называют оператором воздействия, а оператор  при выходной переменной y – собственным оператором.

Математическое определение линейных САР

Выше было сказано, что непрерывные САР подразделяются на линейные и нелинейные. Для линейных систем, в отличие от нелинейных, справедлив принцип суперпозиции, математическая сущность которого заключается в следующем:

Пусть известно, что реакцией САР (рис.2.5) на воздействие g₁(t) является сигнал x₁(t)=Ag₁(t), реакцией САР на воздействие g₂(t) – сигнал x₂(t)=Ag₂(t), …, реакцией на воздействие g_n(t) – сигнал x_n(t)=Ag_n(t), где A – оператор преобразования входной функции в выходную. В роли воздействий g_i(t) могут выступать как управляющие, так и возмущающие воздействия.

САР является линейной, если ее реакция на линейную комбинацию функций (сигналов) g_i(t), i=1,2,…,n

              ,

где k_i – произвольные действительные числа, является также линейной комбинацией сигналов x_i(t), i=1,2,…,n:

.

Проще говоря, реакция линейной системы на сумму сигналов равна сумме реакций на каждый сигнал в отдельности.

Если все элементы САР (АР, ПУ, ОУ) являются линейными, то и САР в целом будет линейной. Наличие же в САР хотя бы одного нелинейного элемента делает систему нелинейной.

Линейные САР подразделяются на стационарные и нестационарные. Нестационарными являются САР, оператор A которых сам является функцией времени. Отметим, что это не противоречит принципу суперпозиции, поскольку САР остается линейной.

Большую часть реальных САР можно считать линейными, разумеется, с наложением при этом некоторых ограничений. Для получения соответствующей линейной модели используется линеаризация всех или некоторых уравнений исходной САР.

Линеаризация динамических САР

Линеаризацией нелинейных дифференциальных уравнений (ДУ) реальной САР является процесс их преобразования в линейные уравнения, суть которого заключается в следующем:

В САР должен поддерживаться некоторый заданный режим работы, в котором входные и выходные величины изменяются по определенному закону. Но из-за наличия возмущающих факторов реальные значения переменных состояния отличаются от заданных значений, причем в нормально работающей системе эти различия достаточно малы. Это позволяет разложить нелинейные функции, входящие в уравнения, в ряд Тейлора в окрестности точки, соответствующей заданному (нормальному) режиму работы САР.