Дифференциальные уравнения и передаточные функции линейных непрерывных систем автоматического регулирования, страница 3

где  – коэффициент передачи усилителя мощности.

Узел сравнения

Составленное ранее уравнение оставляем без изменения:

              .                        (5)

Цепь корректирования

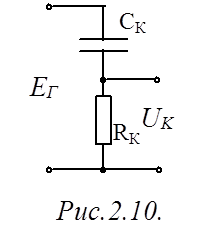ДУ для цепи корректирования (рис.2.10) имеет вид:

         

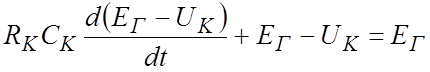
или

                        ,                                  (6)

где  – постоянная времени цепи, с.

Очевидно, цепь корректирования работает только в переходных режимах. В установившихся режимах, когда , правая часть (6) равна нулю.

Передаточные функции

Для установления взаимосвязи между входом и выходом САР используются передаточные функции в операторной форме и передаточные функции в изображениях Лапласа.

Передаточная функция в операторной форме

Передаточной функцией (ПФ) САР или звена в операторной форме называется отношение оператора воздействия к собственному оператору.

Например, пусть САР описывается ДУ:

,              (*)

где  – входное воздействие;   – выходная переменная;

       – оператор воздействия;

       – собственный оператор САР.

Передаточная функция САР в операторной форме, согласно определению, имеет вид:

              .                        (**)

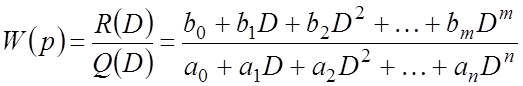Степень полинома знаменателя называют порядком ПФ, а разность между степенями полиномов знаменателя и числителя – относительным порядком ПФ.

Нулями и полюсами ПФ (**) называют нули ее числителя и знаменателя соответственно, то есть корни уравнений  и , где D рассматривается как алгебраическая переменная, а не как оператор. В то же время следует помнить, что ПФ в операторной форме является оператором, и поэтому ее нельзя рассматривать как обычную дробь. В частности, числитель и знаменатель нельзя сокращать на общий множитель, содержащих оператор дифференцирования D.

Для представления ПФ в эквивалентной алгебраической форме используют преобразование Лапласа. Оно особенно удобно при исследовании линейных стационарных систем.

Преобразование Лапласа

Преобразованием Лапласа называют соотношение:

          ,

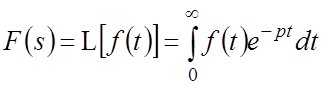которое ставит функции  действительного переменного в соответствие функцию  комплексного переменного ().

Функция , подвергающаяся преобразованию Лапласа, называется оригиналом, и должна обладать следующими свойствами:

·   определена и кусочно-дифференцируема на интервале ;

·   при ;

·  существуют такие положительные числа c и M, что при любом  выполняется неравенство .

Функция  называется изображением. Оператор  называют оператором преобразования Лапласа.

Соотношение

          ,

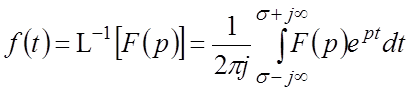определяющее по известному изображению его оригинал, называют обратным преобразованием Лапласа, а оператор  – оператором обратного преобразования Лапласа.

Таблицы соответствия между некоторыми оригиналами и изображения приведены в табл.2.1.

Рассмотрим основные свойства (теоремы) преобразования Лапласа (табл.2.2). Их доказательства несложны, и приводятся в специальной литературе.

Табл.2.1. Преобразования Лапласа [6]

Название функции	f(t)	F(p)	Название функции	f(t)	F(p)
Единичная ступенчатая функция			Синусоида
Единичная импульсная функция		1	Косинусоида
Единичная линейная функция	t		Затухающая синусоида
Степенная функция	tn		Затухающая косинусоида
Экспонента			Расходящаяся синусоида
Экспонента n-го порядка			Расходящаяся косинусоида

Передаточная функция в изображениях Лапласа

Передаточной функцией САР или звена в изображениях Лапласа называется отношение изображения выходной переменной к изображению входной переменной при нулевых начальных условиях, имеющее наименьший порядок.

Таким образом, согласно определению, ПФ в изображениях Лапласа не может иметь равные между собой нули и полюсы, так как в этом случае ее порядок следует понизить, сократив числитель и знаменатель на общий делитель.

Табл.2.2. Теоремы преобразования Лапласа [6]

Название операции	Формулировка теоремы	Название операции	Формулировка теоремы
Умножение оригинала на коэффициент k	, k=const	Чистое запаздывание
Сумма		Начальное значение
Производная		Конечное значение
Производная n-го порядка		Умножение оригинала на экспоненту
Интеграл		Интеграл свертки

Определим ПФ (в изображениях Лапласа) звена, описываемого ДУ (*), применив к обеим частями этого уравнения преобразование Лапласа, и используя свойство линейности преобразования (табл.2.2):

.

Учитывая, что начальные условия нулевые, с помощью табл.2.2 получаем:

.

Отсюда находим передаточную функцию от входа  к выходу :

.                                                                                        (***)

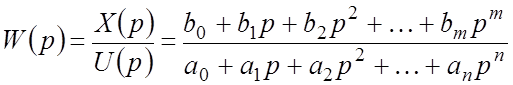Таким образом, ДУ в изображениях Лапласа легко получается из ДУ в операторной форме путем подстановки  и замене переменных их изображениями. Поэтому ПФ  в изображениях Лапласа связана с ПФ  в операторной форме соотношением

          .

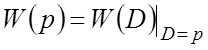При этом после подстановки следует сократить общие множители, если они присутствуют. Обратное соотношение

                   

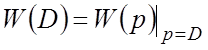
справедлива, если передаточная функция  не имеет равных между собой нулей и полюсов.

Следует отметить очень важные моменты:

1.  Последние два соотношения, устанавливающих соответствие между ПФ некоторой САР (или звена)  в операторной форме и ПФ  в изображениях Лапласа, справедливы только для стационарных САР. Поэтому в общем случае, когда говорят просто о передаточной функции САР или звена, имеют в виду ПФ в изображениях по Лапласу.

2.  При наличии равных между собой нулей и полюсов ПФ  в операторной форме некоторой САР (или звена) ПФ  в изображениях Лапласа не может служить его описанием при произвольных начальных условиях.

Передаточные функции линейных САР

Продолжим рассмотрение примера САР скорости двигателя постоянного тока (рис.2.7). По записанным ДУ (1) – (6) запишем ПФ элементов САР.

Генератор:

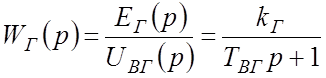              .                        (1’)

Двигатель:

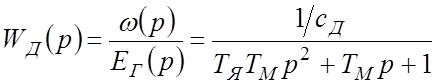              .                        (2’)

Тахогенератор:

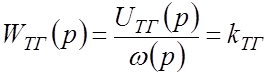              .                        (3’)

Усилитель мощности:

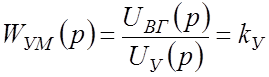              .                        (4’)

Уравнение узла сравнения для изображений:

              .                        (5’)

Цепь корректирования:

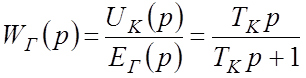                        .                        (6’)

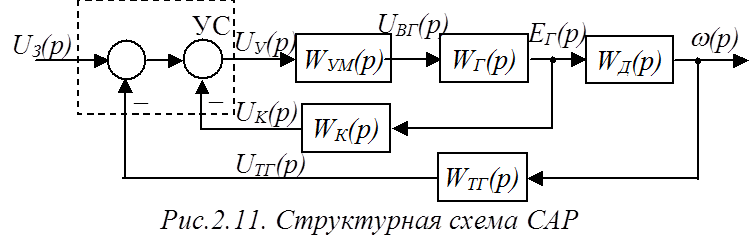
Имея ПФ элементов САР, по блок-схеме (рис.2.8) можно изобразить структурную схему САР (рис.2.11), помещая в каждом блоке соответствующее ему обозначение ПФ (рис.2.11а).