
















Федеральное агентство по образованию
Саратовский государственный технический университет
Кафедра технической кибернетики и информатики
Контрольная работа
по дисциплине
Теория автоматического управления
Выполнил
студент группы УИТ-21
Никандров П.Д.
Проверил
Садомцев Ю.В.
Саратов 2011
Содержание
Техническое задание на проектирование. 3
1. Синтез и анализ непрерывной модели управления. 6
1.1. Составление математической модели объекта управления. 6
1.2. Исследование на управляемость и наблюдаемость. 7
1.3. Составление структурной схемы.. 8
1.4. Исследование возможности решения задачи с помощью простейшего статического регулятора. 10
1.4.1. Построение области устойчивости. 10
1.4.2. Построение области требуемой точности. 12
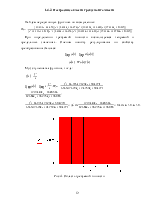
1.4.3. Построение области требуемого быстродействия. 13
1.5. Исследование возможности решения задачи с помощью динамического регулятора. 15
1.6. Анализ замкнутой системы управления с непрерывным регулятором.. 17
2. Синтез и анализ дискретной модели управления. 18
2.1. Составление структурной схемы дискретной системы.. 18
2.2. Составление и анализ замкнутой непрерывно-дискретной системы.. 19
Литература. 20
Приложения. 21
Техническое задание на проектирование
Система предназначена для стабилизации скорости вращения двигателя постоянного тока, работающего при изменяющемся моменте сопротивления нагрузки.
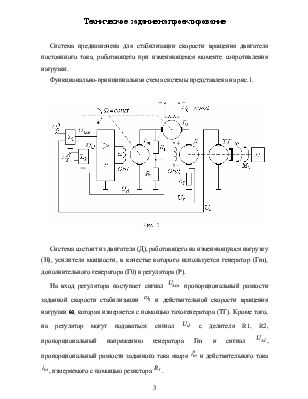
Функционально-принципиальная схема системы представлена на рис.1.
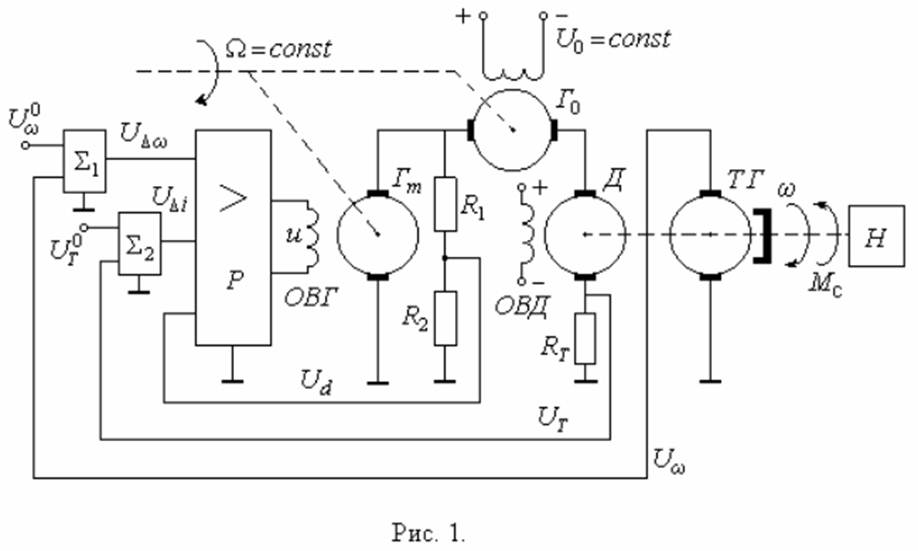
Система состоит из двигателя (Д), работающего на изменяющуюся нагрузку (Н), усилителя мощности, в качестве которого используется генератор (Гm), дополнительного генератора (Г0) и регулятора (Р).
На вход регулятора поступает сигнал ![]() пропорциональный разности заданной скорости
стабилизации
пропорциональный разности заданной скорости
стабилизации ![]() и
действительной скорости вращения нагрузки w,
которая измеряется с помощью тахогенератора (ТГ). Кроме того, на регулятор
могут подаваться: сигнал
и
действительной скорости вращения нагрузки w,
которая измеряется с помощью тахогенератора (ТГ). Кроме того, на регулятор
могут подаваться: сигнал ![]() c делителя R1, R2, пропорциональный
напряжению генератора Гm и сигнал
c делителя R1, R2, пропорциональный
напряжению генератора Гm и сигнал ![]() , пропорциональный разности заданного тока
якоря
, пропорциональный разности заданного тока
якоря ![]() и
действительного тока
и
действительного тока ![]() ,
измеряемого с помощью резистора
,
измеряемого с помощью резистора ![]() .
.
![]()
![]()
![]() Система работает следующим образом.
При номинальной нагрузке
Система работает следующим образом.
При номинальной нагрузке ![]() вал двигателя
вращается с заданной скоростью
вал двигателя
вращается с заданной скоростью ![]() под действием
напряжения с генератора Г0. При этом напряжение с
тахогенератора
под действием
напряжения с генератора Г0. При этом напряжение с
тахогенератора ![]() равно по величине и
противоположно по знаку напряжению задатчика
равно по величине и
противоположно по знаку напряжению задатчика ![]() ,
и с выхода сумматора
,
и с выхода сумматора ![]() сигнал равен нулю. Кроме
того, в этом режиме через двигатель протекает номинальный ток
сигнал равен нулю. Кроме
того, в этом режиме через двигатель протекает номинальный ток ![]() , и напряжение
, и напряжение ![]() на резисторе
на резисторе ![]() равно по величине и
противоположно по знаку напряжению
равно по величине и
противоположно по знаку напряжению ![]() ,
так что на выходе сумматора
,
так что на выходе сумматора ![]() сигнал также
отсутствует. Таким образом, при номинальной нагрузке, если
сигнал также
отсутствует. Таким образом, при номинальной нагрузке, если ![]() , на обмотку возбуждения генератора (ОВГ)
сигнал не подается, и напряжение на выходе генератора
, на обмотку возбуждения генератора (ОВГ)
сигнал не подается, и напряжение на выходе генератора ![]() равно
нулю.
равно
нулю.
При изменении нагрузки на величину ![]() изменяется
скорость двигателя и ток якоря, что приводит к появлению сигналов на входе
регулятора и, следовательно, к появлению напряжения на генераторе
изменяется
скорость двигателя и ток якоря, что приводит к появлению сигналов на входе
регулятора и, следовательно, к появлению напряжения на генераторе ![]() . В результате под действием суммарного
напряжения на генераторов
. В результате под действием суммарного
напряжения на генераторов ![]() скорость двигателя
становится близкой к номинальной.
скорость двигателя
становится близкой к номинальной.
Исходные данные для проектирования приведены в таблице 1.
Таблица 1
|
Ошибка регулирования |
0,4 |
|
Время
регулированиия |
1,5 |
|
Радиус
устойчивости |
0,75 |
|
Индуктивность
ОВ генератора |
6,8 |
|
Индуктивность
ОВ генератора |
97,0 |
|
Коэффициент
между ЭДС генератора и током ОВ генератора |
100,0 |
|
Индуктивность
якоря двигателя |
0,9 |
|
Сопротивление
якоря двигателя |
1,9 |
|
Момент
инерции на валу двигателя |
0,033 |
|
Постоянная
двигателя |
0,42 |
|
Постоянная
двигателя |
0,25 |
|
Коэффициент
передачи тахогенератора |
0,2 |
|
|
8,4 |
|
|
4,2 |
|
Изменение момента сопротивления нагрузки |
1,1 |
Примечания:
1. В качестве объекта управления принять
двигатель с усилителем мощности (генераторы ![]() ).
).
2. При составлении математической модели
объекта сопротивлениями и индуктивностями якорных обмоток генераторов ![]() пренебречь.
пренебречь.
3. При анализе и синтезе системы использовать описание объекта управления в отклонениях от режима стабилизации. При этом считать, что изменение момента сопротивления нагрузки от номинального значения носит ступенчатый характер.
1. Синтез и анализ непрерывной модели управления
1.1. Составление математической модели объекта управления
Запишем математическую модель системы в форме Коши:
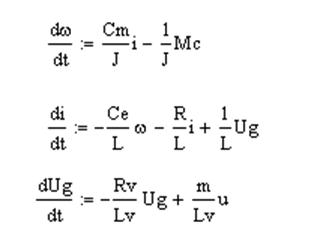

В векторно-матричной форме математическая модель будет иметь вид:
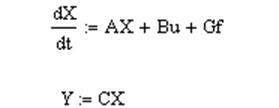
где 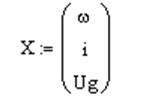 − вектор состояний
системы, f – внешнее возмущение,
− вектор состояний
системы, f – внешнее возмущение,
u- управляющее воздействие, 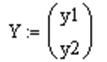 − вектор измеряемых переменных.
− вектор измеряемых переменных.
Численные значения матриц A,B,C,G:
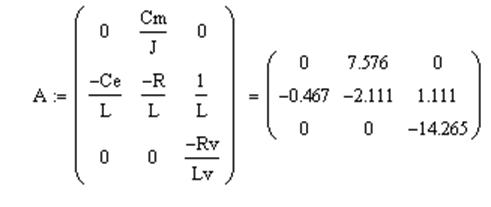
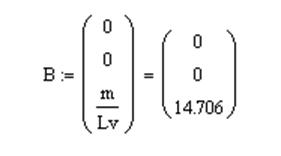
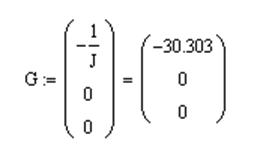
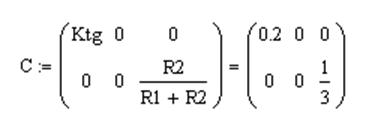
1.2. Исследование на управляемость и наблюдаемость
Критерий управляемости:
![]()
Так как матрица A квадратная, то критерий управляемости может быть переписан в виде:
![]()
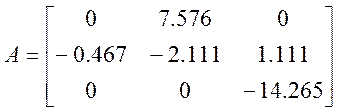
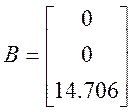
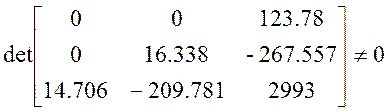
система полностью управляема.
Критерий наблюдаемости:
![]()
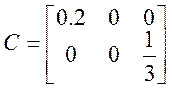
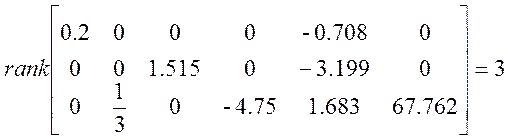
система полностью наблюдаема.
1.3. Составление структурной схемы
Для построения структурной схемы найдём изображения по Лапласу величин w(t), i(t), Ug(t). Для реализации ООС необходимо выполнение условия k1,k2 > 0.
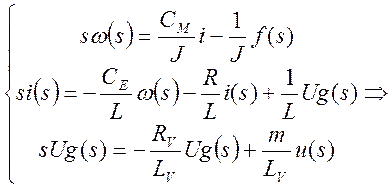
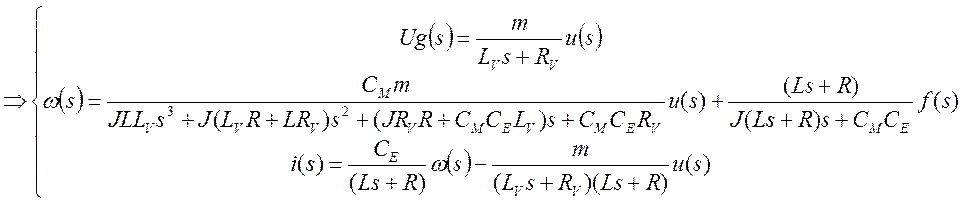
![]()
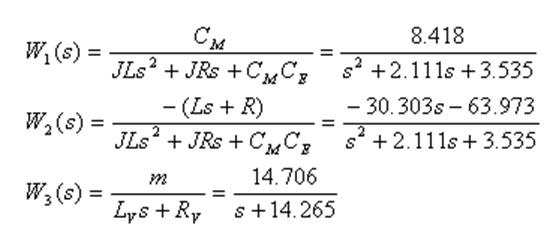
Найдем Wuω по управлению, полагая f=0:
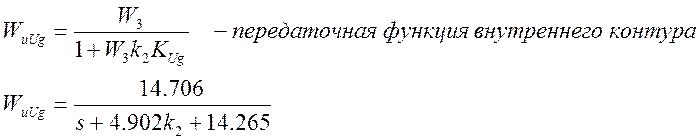
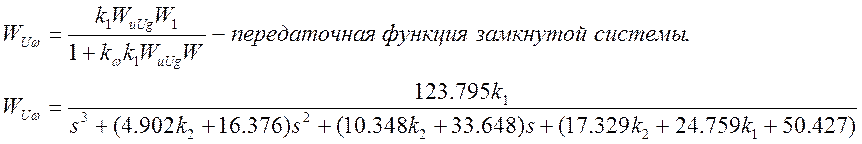
Структурная схема непрерывной замкнутой системы:
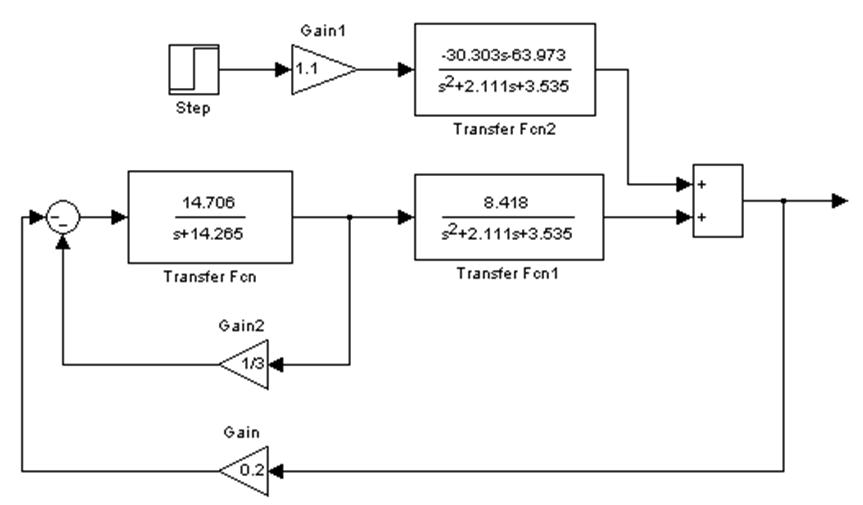
Рис 2. Структурная схема непрерывной системы
1.4. Исследование возможности решения задачи с помощью простейшего статического регулятора
На данном этапе курсовой работы за основу примем статический регулятор, как наиболее простой с точки зрения реализации. Уравнения такого регулятора имеют вид:
![]() ,
,
где k1, k2- искомые коэффициенты передачи
y1, y2 –измеряемые переменные.
Для определения области параметров k1 и k2 используем метод построения областей в плоскости этих параметров, в которых удовлетворяются те или иные требования. При этом в первую очередь строим область, в которой замкнутая система асимптотически устойчива. Далее, определяются условия, при которых выполняются условия точности стабилизации и требования к быстродействию.
1.4.1. Построение области устойчивости
Для устойчивости замкнутой системы, должно выполняться условие устойчивости внутреннего контура.
Запишем характеристический полином внутреннего контура:
![]() ,
,
тогда условием устойчивости будет:
![]()
Очевидно, что при условии реализации отрицательной обратной связи это
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.