условие выполняется при любых 
> 0.
Для определения области устойчивости всей системы, определим ее характеристический полином.
Запишем характеристический полином замкнутой системы:
Для определения параметров k1 и k2 воспользуемся критерием устойчивости Гурвица, для чего составим матрицу Гурвица и найдём главные миноры. Учтем также, что k1 >0 и k2>0 (по условию отрицательной обратной связи).
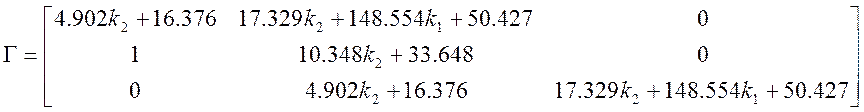
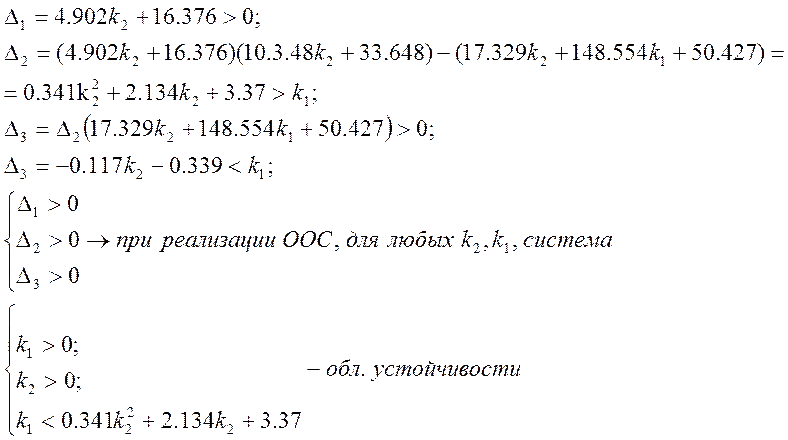
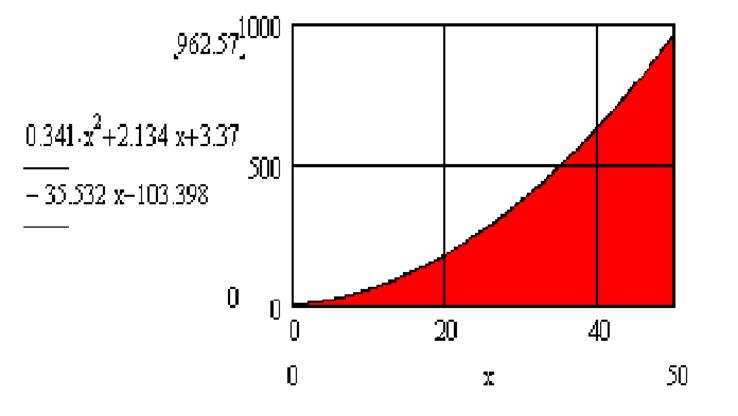
Рис 3. Область устойчивости замкнутой системы
1.4.2. Построение области требуемой точности
Найдём передаточную функцию по возмущению:
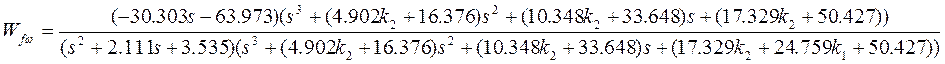
При определении требуемой точности воспользуемся теоремой о предельных значениях. Оценим ошибку регулирования по свойству преобразования Лапласа:
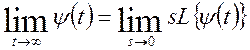
M(s) ступенчатая функция, тогда:
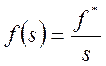
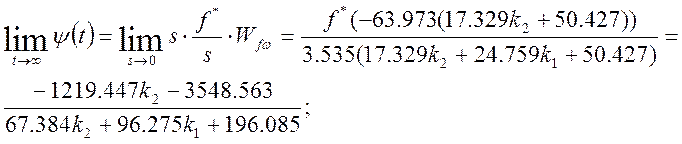
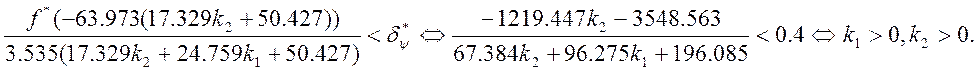
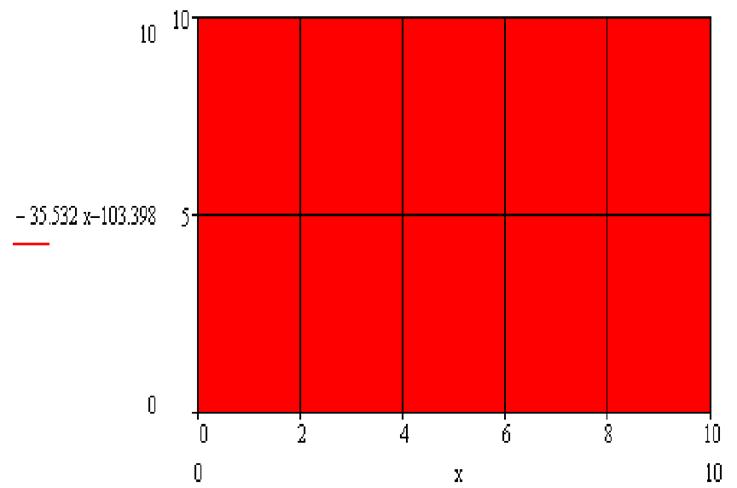
Рис 4. Область требуемой точности
1.4.3. Построение области требуемого быстродействия
Для определения условий и построения области требуемого быстродействия
воспользуемся понятием степени устойчивости 
.
Параметр 
определяется
абсолютной величиной вещественной части ближайшего к мнимой оси корня
характеристического полинома устойчивой замкнутой систему и связан с временем
регулирования приближенным соотношением: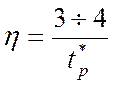 
.
Определим значение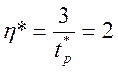 
Найдем область устойчивости для характеристического полинома 
, где 
Произведём замену в характеристическом полиноме 
, где , тогда 
.
Тогда:
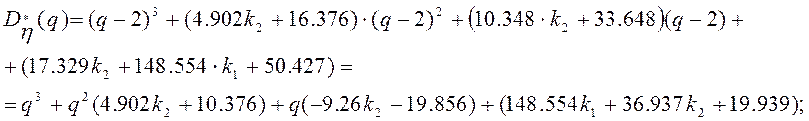
Для определения параметров k1 и k2 воспользуемся критерием устойчивости Гурвица, для чего составим матрицу Гурвица и найдём главные миноры:
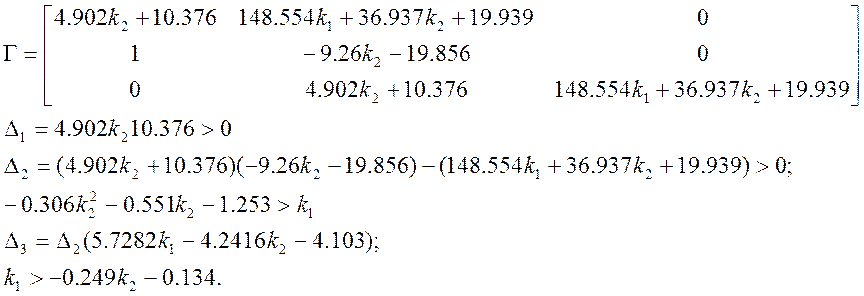
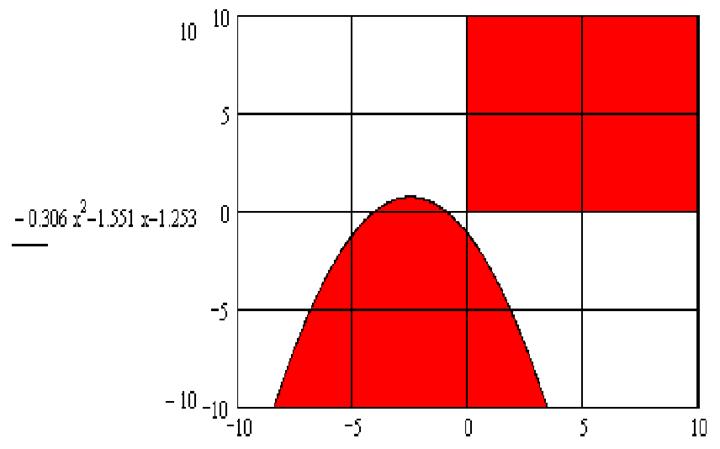
Рис 5. Область требуемого быстродействия
Как видно из рисунка, отображающего найденные условия, для системы со статическим регулятором области быстродействия не существует.
Таким образом, для данной системы не может быть построен статический регулятор, который удовлетворял бы всем требованиям, только частично скорректированный по точности и устойчивости.(k2>0; k1<0.341k22+2.134k2+3.37).
Из полученной области выбираем коэффициенты частично скорректированного статического регулятора k1 = 10 и k2 = 5.
1.5. Исследование возможности решения задачи с помощью динамического регулятора.
Внутренний контур системы имеет большой запас устойчивости, поэтому для построения динамического регулятора методом ЛАЧХ достаточно применить последовательную коррекцию.
Найдем передаточную функцию разомкнутой системы:
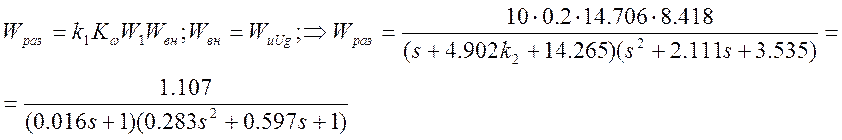
Тогда k=1.107, 20lg(k)=0.883, ω1=3.535, ω2=ω3=63.285.
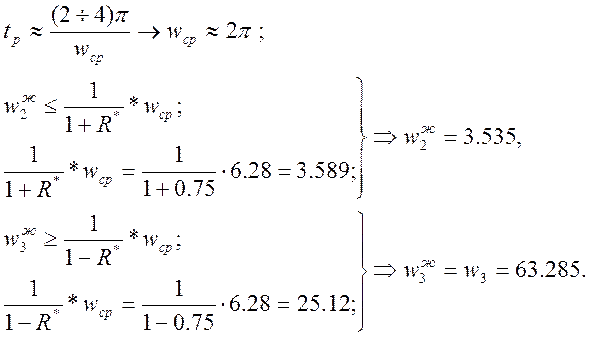
Далее методом ЛАЧХ находим динамический регулятор. Для этого в одной системе координат построим ЛАЧХ исходной разомкнутой системы и желаемую ЛАЧХ с учетом всех требований предъявляемых к заданной системе.
По построенной желаемой ЛАЧХ найдем ПФ Wжраз(s):
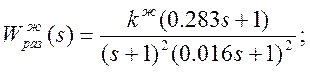
Найдем kж:
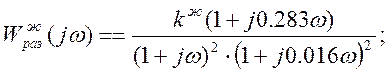
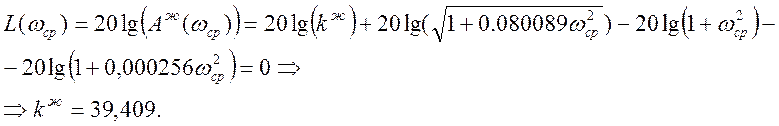
Таким образом получаем:
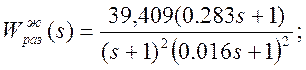
По найденной желаемой передаточной функции разомкнутой системы найдем передаточную функцию последовательного корректирующего устройства:
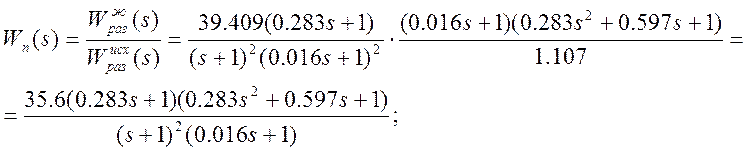
Таким образом структурная схема замкнутой системы с динамическим регулятором имеет вид:
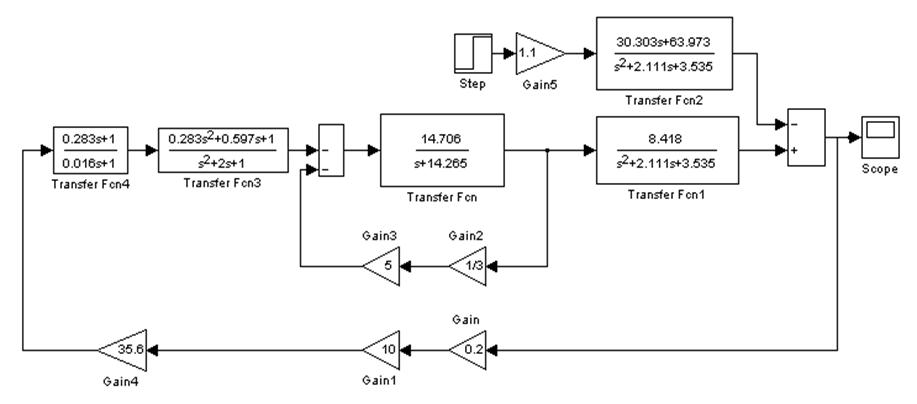
Рис 6. Непрерывная система с динамическим регулятором
1.6. Анализ замкнутой системы управления с непрерывным регулятором
Для анализа частотных показателей качества системы скорректированной с
помощью динамического регулятора построим частотные характеристики для 
. Тогда передаточная
функция с учетом найденных параметров k1 и k2 из области точности и
передаточной функции динамического регулятора будет иметь вид:
Подставляя числовые значения, получим:
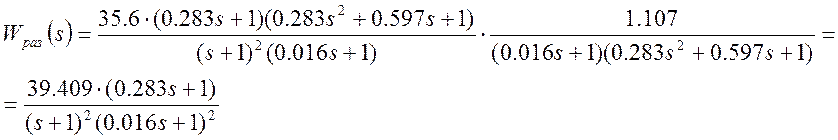
Система, скорректированная с помощью динамического регулятора должна удовлетворять заданным частотным показателям качества. В данном случае показатель радиуса устойчивости R*=0.75.
Для проверки этого условия необходимо построить в комплексной плоскости (U , jV) окружность с центром в точке (-1, j0) и радиусом R.
Для построения годографа нужно произвести замену s=jω в 
и произвести разделение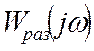 
на вещественную и мнимую часть 
.
Подставляя различные значения ω в 
можно
получить точки годографа. Годограф построен на ЭВМ в среде «Mathlab».
Система удовлетворяет частотным показателям качества, т.к. годограф не заходит в область ограниченную окружностью.
2. Синтез и анализ дискретной модели управления
2.1. Составление структурной схемы дискретной системы
Определим z-передаточные функции соответствующих звеньев непрерывной модели с помощью z-преобразования:
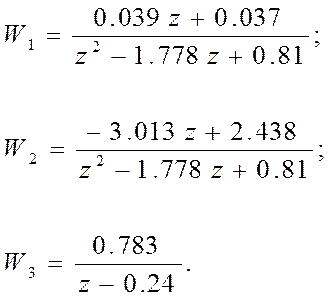
Составим структурную схему дискретной системы с учетом звена запаздывания:
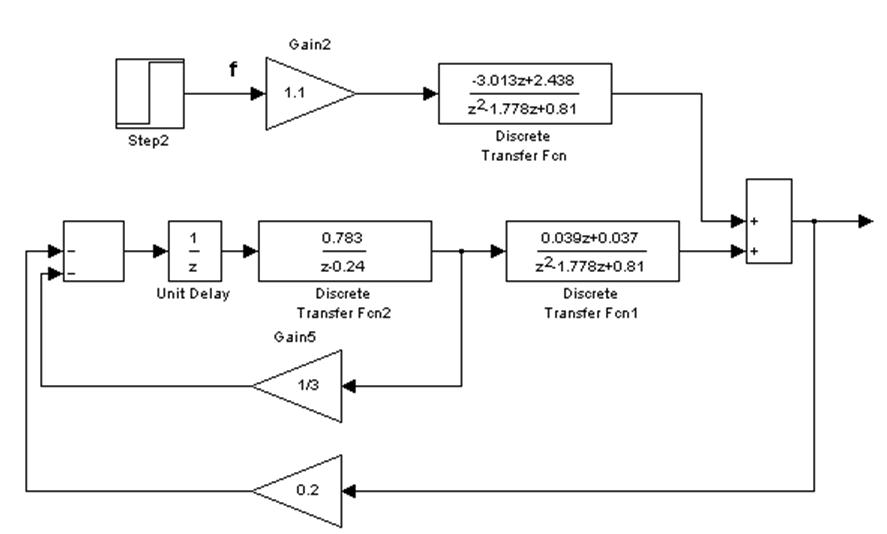
Рис 7. Структурная схема дискретной системы
2.2. Составление и анализ замкнутой непрерывно-дискретной системы
Составим структурную схему непрерывно-дискретной системы. Для этого в найденную ранее непрерывную систему с динамическим регулятором поместим АЦП на выходах датчиков (для каждой измеряемой переменной), а также, учитывая, что управляющий сигнал должен приходить с запаздыванием на один такт, на выходе регулятора необходимо поставить звено запаздывания. Также для корректирующего устройства необходимо найти z-передаточную функцию.
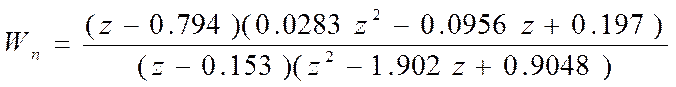
Таким образом, структурная схема непрерывно-дискретной системы имеет вид:
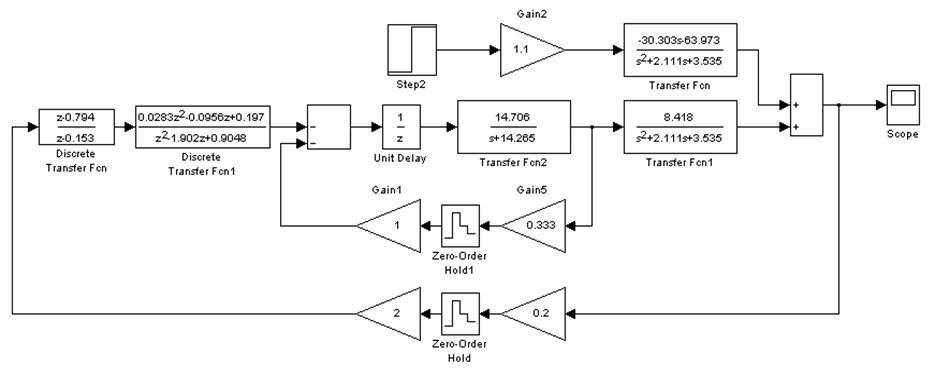
Рис 8. Структурная схема непрерывно-дискретной системы с k1=2, k2=1
Для исследования показателей качества регулирования полученной системы построим график переходного процесса замкнутой системы и годограф разомкнутой системы.
Как видно из построенных характеристик данная система удовлетворяет заданному частотному показателю качества регулирования (показатель радиуса устойчивости R*=0.75) – годограф не заходит в область, ограниченную окружностью с центром в точке (-1, j0) и радиусом R*.
Литература
1. Садомцев Ю.В. Модели систем автоматического управления. Непрерывные системы: Учебное пособие. Саратов. Изд-во СГТУ, 1990.
2. Садомцев Ю.В. Основы анализа дискретных систем автоматического управления: Учебное пособие. Саратов: СГТУ, 1998.
3. Теория автоматического управления. Часть I. Теория линейных систем автоматического управления / Под ред. Воронова А.А. М.: Высшая школа, 1986.
Приложение
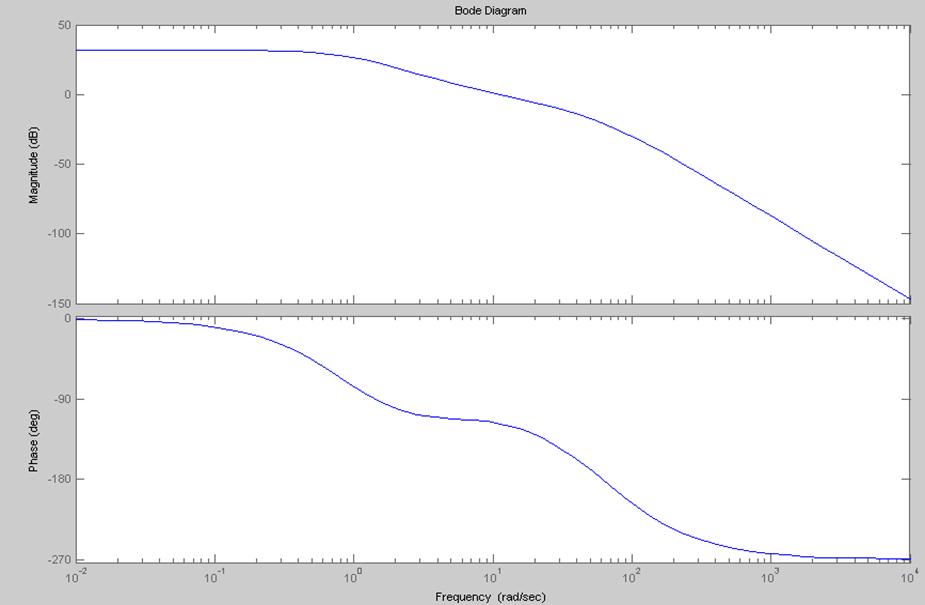
Рис.9. ЛАЧХ и ЛФЧХ разомкнутой непрерывной системы с динамическим регулятором.
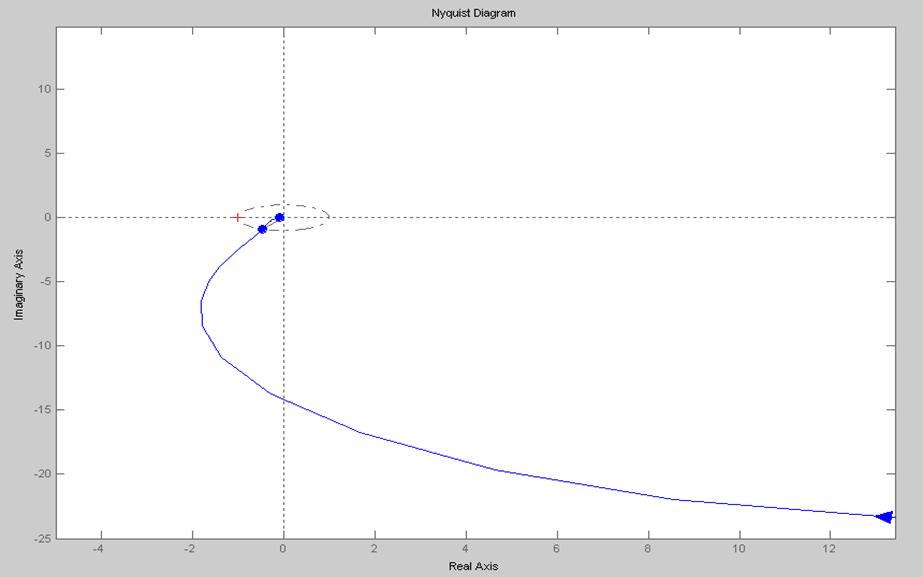
Рис.10. Годограф разомкнутой непрерывной системы с динамическим регулятором.
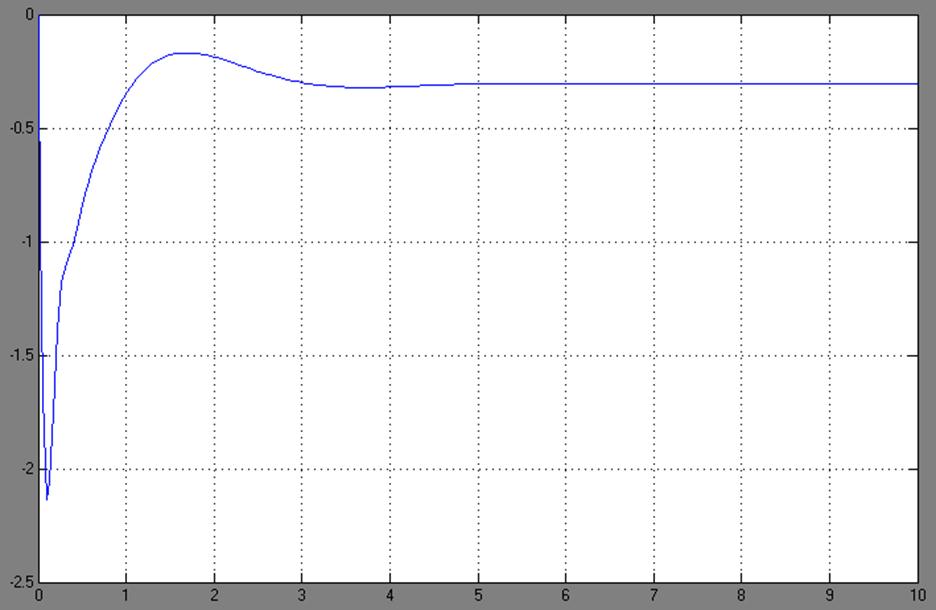
Рис.11. График переходного процесса замкнутой непрерывной системы с динамическим регулятором.
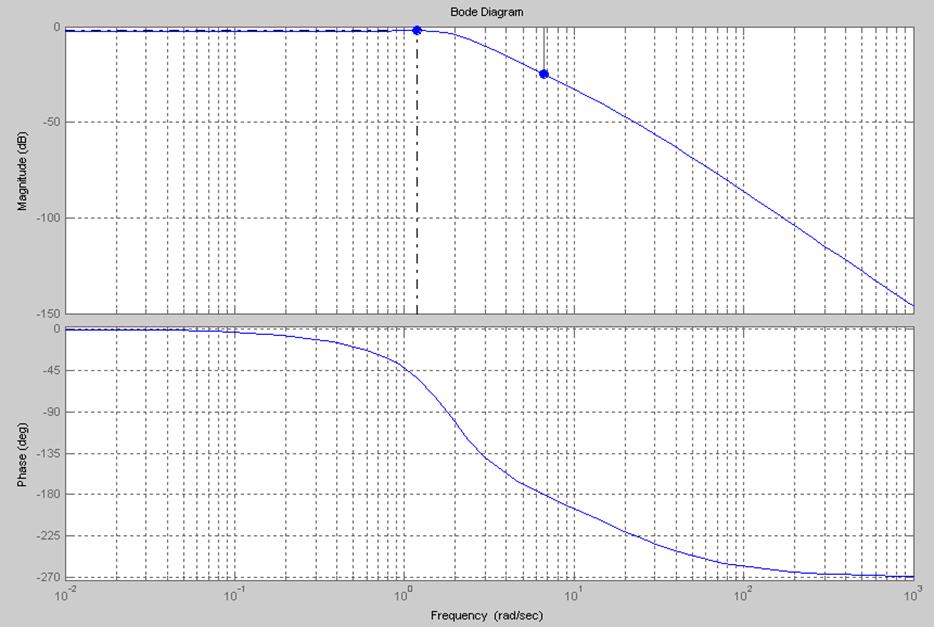
Рис.12. ЛАЧХ и ЛФЧХ разомкнутой непрерывно-дискретной системы с динамическим регулятором.
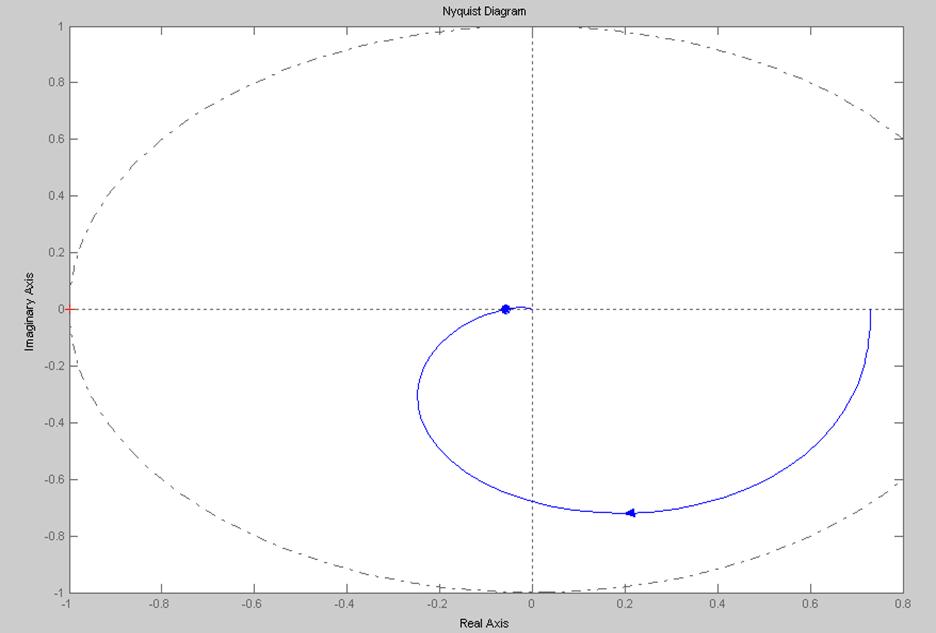
Рис.13. Годограф разомкнутой непрерывно-дискретной системы с динамическим регулятором.
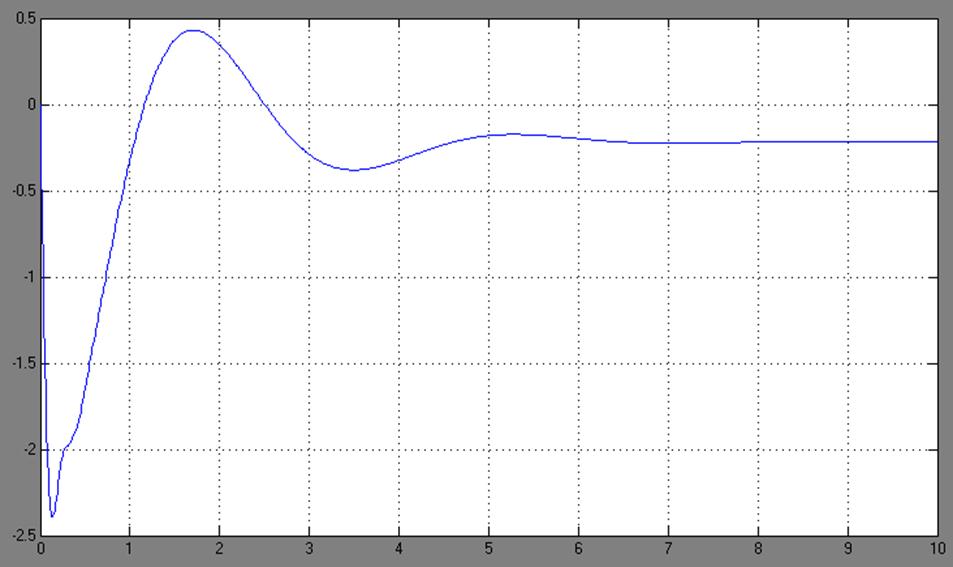
Рис.14. График переходного процесса замкнутой непрерывно-дискретной системы с динамическим регулятором.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.