Математика. Часть 4 (Вычислительная математика): План-конспект лекционного курса, страница 6

1. Постановка задачи и общие положения.

2. Интерполяция. Интерполяционные многочлены в форме Лагранжа
и Ньютона.

3. Погрешность и сходимость интерполяции.

4. Интерполяция сплайнами.

5. Метод наименьших квадратов.

Для практических приложений важными являются следующие задачи. Первая состоит в замене некоторой функции, заданной аналитически или таблично, другой функцией, близкой к исходной, но более простой и удобной для вычислений. Например, замена функции многочленом позволяет получить простые формулы численного интегрирования и дифференцирования; замена таблицы приближающей функцией позволяет получать значения в ее промежуточных точках. Возникает также и вторая задача – восстановление функции на некотором отрезке по значениям функции
в дискретном множестве точек. Кроме того, теория приближения функций является важным вспомогательным аппаратом при численном решении дифференциальных уравнений.

Аппроксимацией (приближением) функции  называется нахождение такой функции  (аппроксимирующей функции), которая была бы близка к заданной. Критерии близости функций  и  могут быть различные.

В том случае, когда приближение строится на дискретном наборе
точек, аппроксимацию называют точечной или дискретной. Когда
аппроксимация проводится на непрерывном множестве точек (отрезке), аппроксимация называется непрерывной или интегральной. Примером такой аппроксимации может служить разложение функции в ряд Тейлора, т.е. замена некоторой функции степенным многочленом.

В общем случае при постановке задачи приближения необходимо действовать по следующему алгоритму:

·  определить, какой класс приближенных функций необходимо
выбрать. Ответ на этот вопрос зависит от вида приближаемой функции и целей, для которых в дальнейшем будет использоваться полученная функция. Широко используются следующие классы функций: многочлены, тригонометрические функции, показательные функции и т.д.;

·  выбрать критерий близости исходной и приближающей функций. В качестве критерия можно выбрать, например, точное совпадение исходной и приближающей функций в узловых точках (интерполяция), минимум суммы квадратов отклонений в узловых точках (метод наименьших квадратов) и др. Как и при выборе класса функций, выбор критерия определяется целью аппроксимации
и может существенно повлиять на результаты;

·  необходимо указать правило, позволяющее с известной степенью точности получить значение функции в промежутках между узлами, в частности, ответить на вопросы, какие узлы использовать при аппроксимации и как их расположить.

Интерполяция

Наиболее часто встречающимся видом точечной аппроксимации является интерполяция.

Пусть на отрезке  задан дискретный набор несовпадаю-
щих точек , , называемых узлами, а также значения функ-
ции  в этих точках. Требуется построить функцию , проходящую через все заданные узлы, т.е. потребуем выполнения равенства

(4.1)

Этот способ построения приближающей функции, при котором
в узлах значения исходной и приближающей функций совпадают, называется интерполяцией. В том случае, когда  одинакова для всей
области интерполяции, говорят, что интерполяция глобальная. В тех случаях, когда между различными узлами функции  различны, говорят
о кусочной или локальной интерполяции.

Найдя интерполяционную функцию, мы можем вычислить значения функции  между узлами (провести интерполяцию в узком смысле слова), а также определить значение функции  даже за пределами
заданного интервала (провести экстраполяцию). Следует иметь в виду, что точность экстраполяции обычно очень невелика.

Наиболее распространен способ линейной интерполяции, в случае
которой  ищется в виде линейной комбинации некоторых базисных функций :

(4.2)

Подставляя функцию (4.2) в равенства (4.1), получаем систему линейных уравнений для определения коэффициентов :

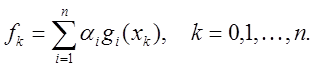
Система функций  должна быть линейно независимой для того, чтобы эта система имела единственное решение.

В качестве базисных функций можно выбрать любую линейно независимую систему функций, но чаще всего выбирают степенные функции . В случае приближения многочленами ищем функцию
в виде многочлена степени n:

(4.3)

где нижний индекс n указывает на степень интерполяционного многочлена. Подставляя в функцию (4.3) значение узлов и используя условие , получаем систему для определения коэффициентов :

(4.4)

многочлен n-ой степени,  многочлен первой Определитель системы (4.4) отличен от нуля, поэтому верно следующее утверждение.

Утверждение. Интерполяционный многочлен степени n для функции , заданной таблично в  точках, существует и единственен.

Существуют некоторые стандартные формы записи интерполяционных полиномов.

Интерполяционный многочлен в форме Лагранжа

Введем вспомогательные многочлены  степени , удовлетворяющие условиям ,  при :

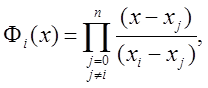
тогда интерполяционный многочлен в форме Лагранжа запишется
в виде

(4.5)

Перечислим основные достоинства многочлена Лагранжа:

·  число арифметических операций, необходимых для построения многочлена Лагранжа, пропорционально  и является наименьшим для всех форм записи;

·  формула (4.5) в явном виде содержит значения функция в узловых точках, что бывает удобно при некоторых вычислениях, в частности, при построении формул численного интегрирования;

·  формула (4.5) применима как для равноотстоящих, так и для
неравноотстоящих узлов;

·  многочлен Лагранжа особенно удобен, когда значения функции меняются, а узлы интерполяции неизменны, что имеет место
во многих экспериментальных исследованиях.

К недостаткам этой формы записи можно отнести то, что с изменением числа узлов приходится все вычисления проводить заново.

Приведем формулы линейной и квадратичной интерполяции по Лаг-
ранжу:

	(4.6)
.	(4.7)