Математика. Часть 4 (Вычислительная математика): План-конспект лекционного курса, страница 2

Пусть  – точное, вообще говоря, неизвестное числовое значение
некоторой величины, а  – известное приближенное числовое значение этой величины, тогда число , про которое известно, что

называют абсолютной погрешностью числа , а величину , про которую известно, что

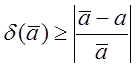
– его относительной погрешностью.

В записи приближенных чисел абсолютная и относительная погрешности указываются так: ; .

Нетрудно показать, что при сложении и вычитании абсолютные
погрешности складываются, а при делении и умножении складываются относительные погрешности.

Погрешность суммы. Пусть , тогда

,

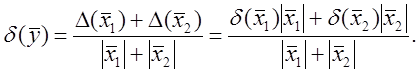
Для n слагаемых , а ,
где , .

Погрешность разности. Пусть , тогда

,

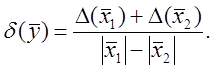
Если величины  и  близки, то относительная погрешность разности может оказаться намного больше, чем  или .

Погрешность произведения. Пусть , тогда

,

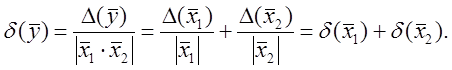
Погрешность частного. Пусть 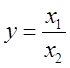, тогда

,

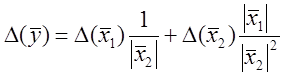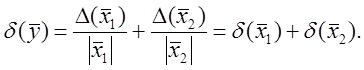
Погрешность функции. Пусть искомая величина является функцией параметров , : . Область G допустимого изменения параметров  известна, требуется получить приближение к y и оценить его погрешность. Если  – приближенное значение, то предельной абсолютной погрешностью называется величина

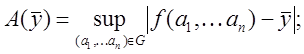
при этом предельной относительной погрешностью называется величина .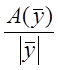

Определение. Значащими цифрами приближенного числа называют все цифры в его записи, начиная с первой ненулевой слева.

Первые n значащих цифр приближенного числа называются верными, если абсолютная погрешность этого числа не превышает половины единицы разряда, соответствующего n-й значащей цифре, считая слева направо.
Излишние сохраненные цифры, помимо верных, называются сомнительными.

Вычислить приближенное число с точностью  означает, что
необходимо сохранить верной значащую цифру, стоящую на n-м разряде после запятой.

На практике возникает надобность в округлении приближенного числа, т.е. замене его числом с меньшим количеством значащих цифр. При этом возникает ошибка округления, которая может накапливаться при расчетах.

Ошибку округления поясним на простом примере. Сначала вычислим n раз корень квадратный из числа 10, а затем n раз возведем полученное число в квадрат. Очевидно, что должно получиться число 10. Однако
результат вычислений на калькуляторе или ЭВМ может существенно
отличаться от теоретического. В таблице приведены результаты вычислений с точностью до 8 верных знаков после запятой.

n	10	20	30	32
n-кратное извлечение корня	1,002251148	1,000002195	1,000000002	1,000000000
n-кратное возведение в степень	9,999997842	9,989948090	8,562917590	1,000000000

Правила округления:

1.  Если первая из отброшенных цифр меньше 5, то оставшиеся десятичные знаки сохраняются без изменений.

2.  Если первая из отброшенных цифр больше 5 либо равна 5 и среди остальных отброшенных цифр есть ненулевые, то к последней
оставшейся цифре прибавляется единица.

3.  Если первая из отброшенных цифр равна 5 и остальные отброшенные цифры нулевые, то последняя цифра не изменяется, если она четная, и увеличивается на единицу, если она нечетная.

Погрешности округления в ЭВМ числа , обусловленные конечностью разрядной сетки, для различных компьютеров могут быть вычислены по формуле

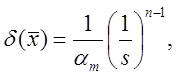
где  – первая значащая цифра; s – основание системы счисления (для десятичной ); n – разрядность компьютера.

Подробнее см.: 1, 3, 4.

Тема 2. Методы решения алгебраических уравнений

Основные вопросы темы

1. Общие положения.

2. Метод деления отрезка пополам.

3. Метод простой итерации.

4. Метод Ньютона. Метод секущих.

Пусть дана непрерывная на некотором промежутке функция .
Необходимо найти принадлежащие этому промежутку корни уравнения

(2.1)

Как правило, алгоритм приближенного метода состоит из двух этапов:

- поиск приближенного значения корня или содержащего его отрезка;

- уточнение приближенного значения до некоторой заданной степени точности.

Иногда ограничиваются только первым этапом. При этом могут
использоваться решения близких задач, графические методы, физические соображения и т.д. На втором этапе для уточнения приближенного значения обычно строится последовательность, элементы которой в пределе сходятся к точному значению корня. Сам метод решения при этом называется итерационным или методом последовательных приближений.

Первый этап не может быть алгоритмизован, т.е. нельзя указать способ, который можно применять ко всем типам уравнений. Однако существует несколько способов, которые можно применять для поиска приближенного корня или отрезка.

В ряде случаев может оказаться полезной теорема из курса математического анализа.

Теорема 1. Если функция  на концах отрезка  принимает значения разных знаков, т.е. , то на этом отрезке содержится по крайней мере один корень уравнения. Если же функция  непрерывна и дифференцируема и ее производная сохраняет знак внутри отрезка , то на этом
отрезке находится только один корень уравнения (2.1).

Если на концах отрезка функция имеет одинаковые знаки, то корни либо отсутствуют, либо их четное число.

Для многочлена n-ой степени 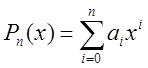 известно, что интервал,
на котором расположены корни , определяется следующим соотношением:

.

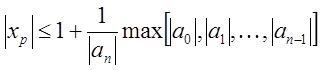Для отделения корня многочлена полезно также использовать следующие теоремы.

Теорема 2. Если все корни уравнения являются действительными числами, то для последовательности коэффициентов   квадрат каждого
некрайнего коэффициента больше произведения соседних с ним коэффициентов, т.е. ,

Теорема 3. Если для каких-либо k выполнено неравенство ,
то многочлен имеет, по крайней мере, пару комплексных корней.

На втором этапе уточнения корня используется два типа методов: прямые и итерационные. В прямых методах корень уравнения может быть найден за конечное, заранее известное число операций. Прямыми методами удается решить некоторые простейшие уравнения.

В итерационных методах корень  определяется как предел последовательности , и решение не может быть найдено за конечное число операций.