Математика. Часть 4 (Вычислительная математика): План-конспект лекционного курса, страница 10

	(6.9)
	(6.10)
	(6.11)

Формулы (6.4)-(6.11) носят название безразностных формул численного дифференцирования.

Применение ряда Тейлора для численного дифференцирования

Можно также находить производные, разлагая функцию  в ряд Тейлора по степени h, где h достаточно мало:

	(6.12)
	(6.13)

Из этих формул получаем

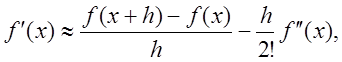
Вычитая соотношение (6.13) из (6.12), получаем

(6.14)

Первые два выражения называются односторонней правой и левой производной, а выражение (6.14) – центральной или симметричной производной.

Складывая соотношения (6.12) и (6.13), получаем для второй производной:

(6.14)

Подробнее см.: 1, 3, 4.

Тема 7. Численное интегрирование

Основные вопросы темы

1. Постановка задачи.

2. Формулы численного интегрирования.

3. Метод Ромберга повышения порядка точности.

В тех случаях, когда при вычислении определенного интеграла

(7.1)

невозможно найти первообразную или она очень сложна для вычислений, обращаются к формулам численного интегрирования. При этом
подынтегральную функцию аппроксимируют более простой функцией,
интеграл от которой может быть легко вычислен. Обычно в качестве
аппроксимирующей функции используют полином в форме Лагранжа,
т.е. , где  – остаточный член интерполяции. Подставляя этот многочлен в (7.1), получаем

Здесь R – остаточный член формулы численного интегрирования или ее погрешность.

Приближая  многочленами различной степени, получают различные формулы численного интегрирования с разной степенью точности.
В случае полинома нулевой степени метод численного интегрирования
называют методом прямоугольников (средних), в случае полинома первой степени – методом трапеций, в случае полинома второй степени – методом Симпсона.

Формулы численного интегрирования

Заменим  на многочлен нулевой степени, проходящий через середину отрезка – точку . Тогда площадь криволинейной трапеции под функцией  можно заменить площадью прямоугольника, т.е.

(7.2)

Погрешность формулы прямоугольников (7.2) составляет

(7.3)

Разлагая  в ряд относительно середины отрезка, получим приближенное значение

	(7.4)

Значение остаточного члена в формуле прямоугольников может быть велико, так как разность  может быть достаточно большой. Для
повышения точности введем сетку

с достаточно малым шагом  и применим формулу прямоугольников на каждом шаге сетки. Тогда получим обобщенную формулу прямоугольников

(7.5)

с величиной остаточного члена

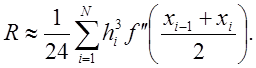
Если шаг сетки постоянен, то эти формулы упрощаются

(7.6)

Для справедливости оценки величины R необходимо существование непрерывной второй производной; если  – кусочно-непрерывна,
то можно сделать оценку сверху, заменяя  на максимальную величину , т.е.

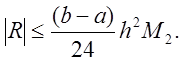
В том случае, когда  задана таблично, ее значение в середине
отрезка интервала может быть неизвестно. Это значение находится, как правило, интерполированием, что приводит к ухудшению точности формулы прямоугольников.

В случае таблично заданных функций удобнее в качестве узлов
интерполяции выбрать начало и конец отрезка интерполирования, т.е.
заменить функцию  многочленом Лагранжа первой степени (прямой линией). Это значит, что вместо площади криволинейной трапеции мы
будем искать площадь прямоугольной трапеции. Приближенное значение интеграла вычисляется по формуле трапеций и равно

,

имея в виду, что , .

Погрешность интегрирования вычисляется по формуле

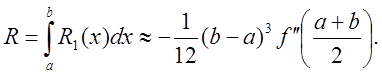
Для повышения точности введем сетку . Подсчитывая значение интеграла для каждого интервала и суммируя эти значения, получаем обобщенную формулу трапеций и формулу для вычисления
погрешности:

(7.7)

Эти формулы упрощаются на сетке с постоянным шагом h:

(7.8)

Аналогично, как и для формулы прямоугольников, можно получить оценку для R

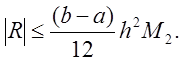
Таким образом, формула трапеций (как и формула прямоугольников) имеет второй порядок точности относительно шага сетки, и погрешность асимптотически стремится к нулю при  с точностью до членов более высокого порядка малости.

Для повышения порядка точности формулы численного интегрирования заменим  параболой – интерполяционным многочленом Лагранжа второй степени, выбирая в качестве узлов интерполяции концы и середину отрезка интегрирования: , , .

В этом случае, проинтегрировав многочлен, получим формулу Симпсона и ее погрешность

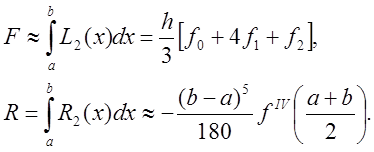
Как и в предыдущих двух случаях, для повышения точности введем сетку с достаточно малым шагом. Суммируя значения интегралов для каждого интервала, получаем обобщенную формулу Симпсона, которая
на равномерной сетке имеет вид

	(7.9)
	(7.10)

Таким образом, формула парабол имеет четвертый порядок точности относительно шага сетки. Вводя обозначение 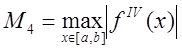, получим оценку сверху для погрешности

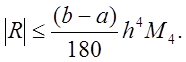
Метод Ромберга повышения порядка точности

В вычислениях с помощью формул численного интегрирования
результат получается тем точнее, чем с большим числом узлов используется сетка. Однако при этом формулы оказываются достаточно громоздкими. Метод Ромберга позволяет получить более высокий порядок точности
без значительного увеличения узлов.

Пусть для вычисления величины   имеется функция , дающая возможность приближенного расчета величины  на равномерной сетке с шагом h. Значение остаточного члена можно представить в виде

(7.11)

где p – порядок точности расчетной формулы, а  – главный член погрешности. Например, для формулы прямоугольников и трапеций , а для формулы парабол .

Если провести расчет на другой сетке с шагом rh, приближенное значение  величины  окажется другим. В этом случае остаточный член примет вид

(7.12)

Значение главного члена погрешности определяется вычитанием
выражения (7.12) из (7.11):

(7.13)