Математика. Часть 4 (Вычислительная математика): План-конспект лекционного курса, страница 20

Приведем несколько примеров барьерных функций. Например,
если , где  непрерывна на X, ,
то в качестве барьерной функции можно взять ,
или , или . Если же , то можно принять , или .

Пусть некоторое множество  и его барьерная функция уже заданы. Введем функции

где  – положительная последовательность барьерных коэффициентов, сходящаяся к нулю. Обозначим , тогда последовательность  определяется из условий

(12.14)

где . Если окажется, что , то в (12.14) допускается .

Для поиска  при фиксированном k и определения  
из условий (12.14) могут быть использованы различные методы минимизации. В частности, если  и , то можно воспользоваться градиентным методом:

Поскольку , то при достаточно малых  и точка  также попадет в , и мы избавимся от проблем с границей множества. Нужно лишь следить за величиной шага  и уменьшать его,
если .

Метод барьерных функций иногда называют методом внутренних штрафов или методом внутренней точки. Теперь сформулируем утверждение о сходимости метода.

Теорема 3 [2]. Пусть , , и

.

Пусть  – барьерная функция подмножества , а последовательность  определена  условиями (12.14). Тогда

Кроме того, если X ограничено и замкнуто, а  полунепрерывна снизу
на X, то  сходится к .

В заключение приведем пример барьерной функции в случае, когда

здесь  – заданное множество из , функции  непрерывны
на . Положим

 хотя бы для одного .

Тогда барьерная функция может быть задана выражениями

.

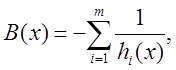
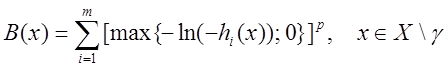О методах случайного поиска

Метод случайного поиска, в отличие от ранее рассмотренных методов, характеризуется намеренным введением элемента случайности в алгоритм поиска. Будем строить последовательность  по правилу:

(12.15)

где  – некоторая положительная величина;  – некоторая реализация n-мерной случайной величины ξ с известным законом распределения. Например, координаты  случайной величины ξ могут представлять независимые случайные величины, распределенные равномерно на отрезке .

Приведем несколько вариантов метода случайного поиска для поиска минимума функции  на множестве , предполагая, что приближение  уже известно.

Алгоритм с возвратом при неудачном шаге. Задается некоторая величина шага t. С помощью датчика случайного вектора получают некоторую его реализацию ξ и в пространстве  определяют точку , . Если  и , то сделанный шаг считается удачным, и полагается , а шаг t  увеличивается вдвое. Если  или же ,
то сделанный шаг считается неудачным и полагается , а шаг t уменьшается вдвое.

Если окажется, что  для достаточно большого N, то точка  может быть принята в качестве приближения искомой точки минимума.

Алгоритм наилучшей пробы. Берутся какие-либо s реализаций  случайного вектора ξ и вычисляются значения функции  
в тех точках , которые принадлежат множеству X.
Затем полагается , где  определяется условием

.

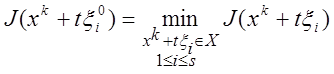Величины  являются параметрами алгоритма и могут меняться в процессе поиска минимума.

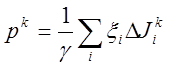Алгоритм статистического градиента. Берутся какие-либо s реализаций  случайного вектора ξ и вычисляются разности  для всех . Затем полагают , где сумма берется по всем тем i, , для которых . Если , то принимается . Если же , то повторяют описанный процесс с новым набором реализаций случайного вектора ξ. Величины  является параметрами метода, который может варьироваться в процессе вычислений. Вектор  называют статистическим градиентом. Если ,  и векторы  являются неслучайными
и совпадают с соответствующими единичными векторами , то описанный алгоритм превращается в разностный аналог градиентного метода.

В описанных вариантах метода случайного поиска предполагается, что закон распределения вектора ξ не зависит от номера итерации. Такой поиск называют случайным поиском без обучения. Такие алгоритмы
не обладают способностью анализировать результаты предыдущих итераций и выделять направления, более перспективные в смысле убывания минимизируемой функции, и сходятся медленно.

Между тем ясно, что более эффективно на каждой итерации учитывать накопленный опыт поиска минимума на предыдущих итерациях
и перестраивать вероятностные свойства поиска так, чтобы более перспективные направления вектора ξ становились более вероятными. Иначе говоря, желательно иметь алгоритмы случайного поиска, которые обладают способностью к самообучению и самоусовершенствованию в процессе поиска минимума в зависимости от конкретных особенностей минимизируемой функции. Такой поиск называется случайным поиском с обучением.
Обучение алгоритма осуществляется посредством целенаправленного
изменения закона распределения вектора ξ в зависимости от результатов предыдущих итераций таким образом, чтобы “хорошие” направления,
по которым функция убывает, стали более вероятными, а другие направления – менее вероятными. Подробнее эти методы случайного поиска
с обучением и без обучения и вопросы их сходимости обсуждаются в 2, 6, 7.

Подробнее см.: 2, 6, 7.

Тема 13. Вариационное исчисление

Основные вопросы темы

1. Постановка задачи и основные определения.

2. Простейшая вариационная задача.

На практике существуют задачи оптимизации, в которых не удается описать качество выбранного решения с помощью целевой функции.
В этих задачах критерий зависит от функции, определить которую необходимо так, чтобы критерий принял минимальное или максимальное значение.

Вариационными задачами называются задачи о поиске экстремума функционалов, т.е. величин, численное значение которых определяется выбором одной или нескольких функций.

Приведем пример такой задачи. Пусть на плоскости  заданы две точки  и . Требуется соединить эти две точки гладкой кривой (рис. 5).

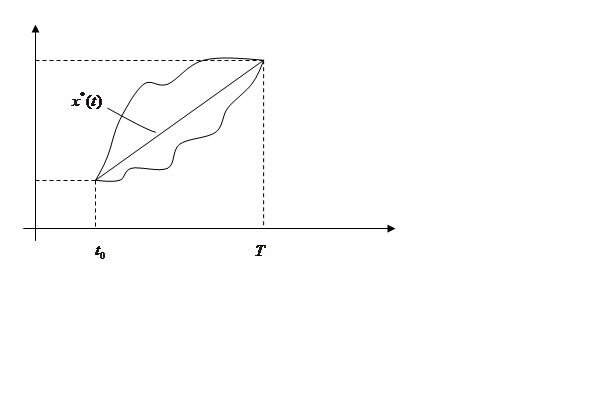
Рис. 5

Длина кривой, соединяющей две заданные точки, находится по формуле

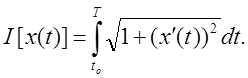
Таким образом, решение задачи сводится к определению такой непрерывной функции , имеющей на отрезке  непрерывную производную и удовлетворяющей заданным граничным условиям  
и , на которой критерий  примет минимальное значение. Критерий зависит от функции  и представляет собой функционал. Очевидно, решением является прямая , соединяющая две заданные точки.