Математика. Часть 4 (Вычислительная математика): План-конспект лекционного курса, страница 19

(11.12)

где последовательности ,  по-прежнему удовлетворяют условиям (11.11). Сходимость метода (11.12) можно ускорить, если длину
шага  менять лишь при изменении знака , сохраняя  постоянным в остальных случаях.

При некоторых предположениях относительно функции  и вероятностных характеристиках случайной величины  можно доказать
сходимость по вероятности последовательности , определяемой формулами (11.10) или (11.12), к точке глобального минимума  на .

Заметим, что скорость сходимости методов стохастической аппроксимации обычно значительно меньше детерминированных методов. Различные варианты метода стохастической аппроксимации и других методов стохастического программирования, а также различные их приложения можно найти в [9].

Подробнее см.: 2, 7.

Тема 12. Численные методы условной оптимизации

Основные вопросы темы

1. Необходимые и достаточные условия минимума.

2. Метод условного градиента.

3 Метод барьерных функций.

4. О методах случайного поиска.

Сначала рассмотрим задачу поиска минимума функции с ограничениями в виде равенств

,	(12.1) (12.2)

при этом предполагается, что функции  и  определены
и имеют непрерывные частные производные на всем пространстве .

В тех случаях, когда систему (12.2) удается преобразовать к эквивалентному виду

(12.3)

выразив s переменных через остальные, рассматриваемую задачу
на условный экстремум можно свести к задаче на безусловный экстремум функции

которую можно исследовать по схеме, описанной в теме 11. Однако этот подход имеет ограниченное применение из-за того, что явное выражение вида (12.3) одной группы переменных через остальные переменные удается получить лишь в редких случаях.

Более общий подход к исследованию задачи поиска дифференцируемой функции  при ограничениях (12.2) дает метод множителей
Лагранжа. Этот метод заключается в следующем. Вводится функция
Лагранжа

,

(12.4)

где  и называется вектором множителей Лагранжа. Этот вектор подчиняется дополнительному условию нормировки

(12.5)

Если векторы  линейно независимы, то условие нормировки (12.5) заменяется на более простое .

Теорема 1 [2]. Пусть: 1) функции ,  дважды непрерывно дифференцируемы в точке ; 2) точка  удовлетворяет условиям (12.5) и

;

(12.6)

3) квадратичная форма  для матрицы вторых производных функции  такова, что

(12.7)

при всех u, для которых

(12.8)

Тогда в точке v функция  на X имеет локальный минимум.

Теорема 1 дает необходимые (12.6) и достаточные условия (12.7)–(12.8) условия минимума в задаче (12.1)–(12.2). Если система (12.6) имеет решения  такие, что , то задачу минимизации  при условиях (12.2) называют регулярной (невырожденной) в точке v. В регулярной задаче можно считать .

Метод множителей Лагранжа может быть применен для решения
задач с ограничениями типа неравенств, однако в этом случае он становится достаточно сложным и неудобным для использования.

Замечание. У множителей Лагранжа имеется экономическая интерпретация. Пусть одно из ограничений имеет вид , тогда оптимальное значение  при изменении  на единицу равно , где  – значение множителя Лагранжа, соответствующего этому ограничению.
Если , то  нечувствительно к изменению правой части соответствующего ограничения.

Далее рассматриваются несколько методов решения задачи условной оптимизации. Описание других численных методов можно найти в [2, 7].

Метод условного градиента

Этот метод предназначен для решения задачи

,

(12.9)

где X – выпуклое замкнутое ограниченное множество из , функция  является непрерывно дифференцируемой. Пусть известно приближение , тогда следующее приближение будем искать в виде

(12.10)

где величина  определяется из условий

(12.11)

В зависимости от способа выбора  в (12.10) можно получить различные варианты метода. Будем задавать эти величины априорно из условий

(12.12)

например, . Можно задать  и проверять условие монотонности , а затем при необходимости дробить  до тех пор, пока не выполнится условие монотонности. Возможны и другие способы выбора  (см. 2, c. 293).

Рассмотрим сходимость метода условного градиента.

Теорема 2 [2]. Пусть X – выпуклое замкнутое ограниченное множество
из , функция  и ее градиент удовлетворяет условию Липшица
на множестве X с постоянной L

.

Тогда при любом  для последовательности , определяемой условиями (12.10)–(12.12) выполнено:

1)  сходится к некоторой стационарной точке;

2) если  является выпуклой на X, то справедливы равенства

.

(12.13)

Если при этом , , то

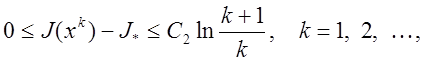
а если ,  , то

здесь  – некоторые положительные постоянные.

Метод барьерных функций

В методе барьерных функций минимизирующая последовательность  строится так, чтобы каждый член последовательности лежал вне некоторого заданного запрещенного подмножества . В качестве
запрещенного множества  может служить, например, граница  множества X или какая-нибудь часть границы. Дело в том, что при применении того или иного метода решения задачи (12.1) при  может оказаться, что каждое получаемое приближение  будет принадлежать . Однако если структура границы множества слишком сложна, то реализация такого метода может потребовать большого объема вычислений и, кроме того, сходимость метода может оказаться очень медленной. В таких случаях можно попробовать как-то построить “барьер” вблизи всей границы  или какой-нибудь ее части  (или какого-
нибудь другого заданного подмножества ), который исключил бы возможность попадания очередного приближения  на .

Определение. Пусть  – некоторое подмножество из X. Функцию  назовем барьерной функцией подмножества , если  определена,
конечна и неотрицательна во всех точках , причем  для всех последовательностей , которые сходятся к какой-либо точке .

Если , то будем считать, что .