Вероятность того, что за время ∆t система не освободится, т. е. останется в S1, по тому же закону Пуассона, но с
интенсивностью завершения обслуживания заявок 
, равна e–µ∆t. (Это вероятность того, что за время ∆t не
произойдет окончания обслуживания заявки.)
Вероятность того, что за ∆t система перейдет из S1 в S0, равна вероятности завершения обслуживания заявки за ∆t 1 – e–µ∆t .
При µ∆t <<1 1 – e–µ∆t ≈ µ∆t .
Этой вероятностью на рис. 15,б помечена дуга из состояния S1 в состояние S0.
Следовательно,
Р(В) = P1(t) µ∆t
Это вероятность того, что система находилась в состоянии S1 и перешла в S0, так как обслуживание заявки закончилось за время ∆t.
Таким образом:
P0(t +∆t ) = P0(t)(1– λ∆t) + µP1(t)∆t = P0(t) – λ∆tP0(t) + µP1(t)∆t.
Перенесем P0(t) в левую часть и разделим обе части на ∆t
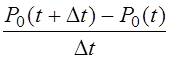= – λP0(t) + µP1(t).
При ∆t 
0 получаем
P0’(t) = – λ P0(t) + µ P1(t).
Рассуждая аналогично, для Р1(t) получим
P1’(t) = λ P0(t) – µ P1(t).
В результате мы получили систему дифференциальных уравнений, описывающих поведение вероятностей состояний системы во времени.
Размеченный граф, полученный в процессе составления системы дифференциальных уравнений, показан на рис. 15,б.
Система дифференциальных уравнений уже не содержит интервала времени ∆t, поэтому граф переходов системы можно упростить, представив его в виде, показанном на рис. 15,в.
По графу переходов рис.15,в можно составить систему дифференциальных уравнений следующим образом:
В левой части записываем производную вероятности нахождения системы в соответствующем состоянии. В правой части для каждой стрелки, связанной с этим состоянием, записываем произведение интенсивности на вероятность состояния, из которого стрелка выходит. Перед произведением ставим знак –, если стрелка выходит из рассматриваемого состояния, ставим +, если стрелка входит в состояние.
Итак, получили систему уравнений:
P0’(t) = – λ P0(t) + µP1(t);
P1’(t) = λ P0(t) – µP1(t).
Кроме того, вероятности удовлетворяют условию
P0(t) + P1(t) = 1.
Для решения этой системы воспользуемся преобразованиями Лапласа.
Нам потребуются:
Прямые преобразования
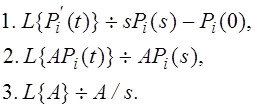
Здесь Pi(0) – начальное значение Pi(t).
Обратные преобразования
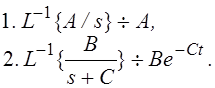
Примечание. Прямое преобразование Лапласа преобразует систему дифференциальных уравнений, описывающих зависимость вероятностей состояний системы от времени, в систему алгебраических уравнений. Обратное преобразование переводит результаты решения в функции времени.
Решим эту систему при начальных условиях
P0(0) = 1; P1(0) = 0.
После преобразования получим
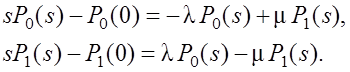
Подставим начальные значения вероятностей и запишем уравнения в упорядоченном виде
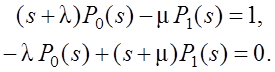
Решение будем искать по правилу Крамера (через определители)
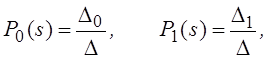
где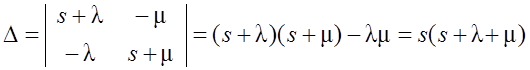 
– определитель
системы,
– определитель
для вычисления P0(s),
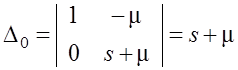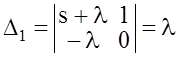– определитель
для вычисления P1(s).
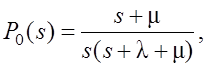(1)
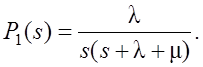
Чтобы применить обратные преобразования Лапласа, выражение (1) для P0(s) надо представить в виде суммы простых дробей
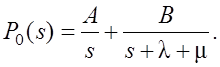(2)
Для этого заготовку суммы (2) приведем к виду полученного решения (1)
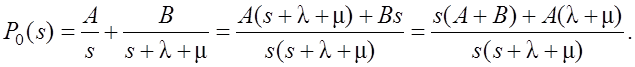(3)
Сравниваем коэффициенты при степенях s в числителях (1) и (3), находим
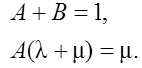
Решая эту систему, получаем
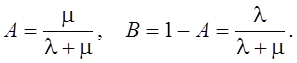
Таким образом,
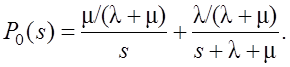
Применив обратное преобразование, получаем
Р0(t) =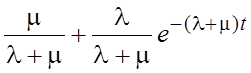
.
Вероятность P1(t) найдем из выражения
P1(t) = 1 – P0(t).
Р1(t) =1 –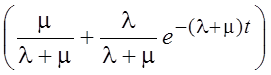 
=
.
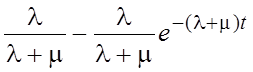При t = 0: P0(0) = 1; P1(0) = 0.
При t = ∞ – наступает стационарный режим
P0(∞) =
;
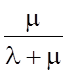P1(∞) =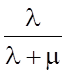 
.
При начальных условиях
P0(0) = 0; P1(0) = 1 получим такое решение
P0(t) =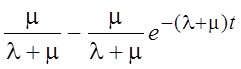 
, (4)
P1(t) =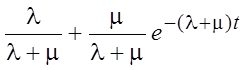 
.
Как долго будет существовать неустановившийся режим?
Обозначим относительную ошибку символом 
(см. рис. 16)
,
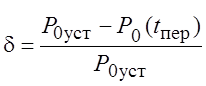где P0уст =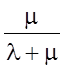 
.
Из уравнения (4) получаем
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.