можем ввести допущение
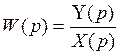
Теперь свяжем нашу функцию с параметрами уравнения (*)
![]()
![]()
Пользуясь свойством линейности найдем изображение левой части уравнения (*)
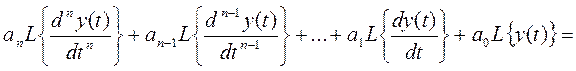
Теперь преобразуем правую часть уравнения (*):
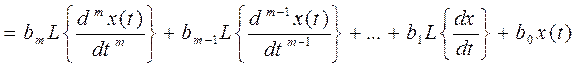
приравняем левую и правую части уравнения к изображению, это даст уравнение для получения передаточной функции:
![]()
![]()
пользуясь теоремой об дифференциальном интеграле, запишем
![]()
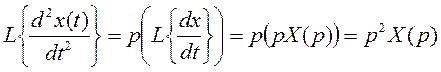
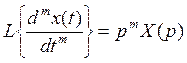
![]() уравнение
получилось алгебраическое, в котором Y(p) и X(p)
можно вынести за скобку
уравнение
получилось алгебраическое, в котором Y(p) и X(p)
можно вынести за скобку
![]()
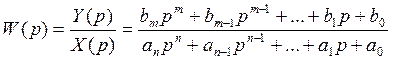
передаточная функция линейного звена W(p) является дробно-рациональной функцией от p и содержит коэффициенты дифференциального уравнения исходно-описывающего это звено
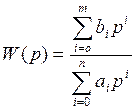 .
.
Ограничения:
1. Понятие передаточной функции справедливо только для линейных звеньев
2. Начальные условия на сигнал были нулевыми.
Теорема Пезу.
Если
полином вида: ![]() имеет п- корней
(
имеет п- корней
(![]() )
)
![]() i=1…n
i=1…n
Аналогично
![]()
![]() - нули переходной функции
- нули переходной функции
![]() - полюса переходной функции
- полюса переходной функции
2.5Временные характеристики звеньев.
Для изучения свойств элементарных звеньев удобно использовать типовые воздействия. По характеру отклика на эти воздействия мы можем судить об их динамических свойствах.
1.Переходная функция
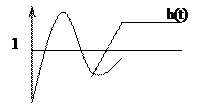
Переходная функция h(t) есть функция, описывающая реакцию системы (звена) на единичное ступенчатое воздействие при нулевых начальных условиях
h(t)![]() x(t)=1(t)
x(t)=1(t)
 |
|||
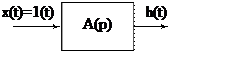 |
|||
![]()
График переходной функции – кривая зависимости функции h(t) от времени t – называют переходной или разгонной характеристикой.
Свяжем переходную функцию с передаточной, для этого найдем преобразование Лапласа:
L{x(t)} = L{1(t)}
= ![]()
Y(p) A(p)X(p)
= 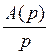
h(t) = L-1 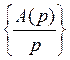
Например:
W(p)=![]()

![]()
Y
М
Мы приложили постоянный ступенчатый сигнал
М(t)=1(t)
Чему будет равно ![]()
![]()
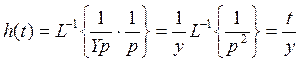
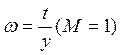
![]()
![]()
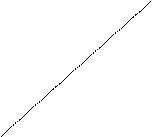
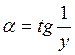
![]()
![]()
![]() t
t
2.Весовая функция
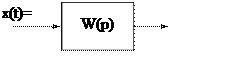 Весовой
или импульсной переходной функцией системы называют функцию, описывающую
реакцию звена на единичное импульсное воздействие при нулевых начальных
условиях; обозначают эту функцию
Весовой
или импульсной переходной функцией системы называют функцию, описывающую
реакцию звена на единичное импульсное воздействие при нулевых начальных
условиях; обозначают эту функцию ![]() .
.
![]()
![]()
![]()
Определим связь между передаточной и весовой функцией:
![]() - входной сигнал
- входной сигнал
![]()
![]() - выходной сигнал
- выходной сигнал
Как видим изображение выходной функции равно передаточной функции
![]()
![]()
Рассмотрим пример:
Нам
дана передаточная функция 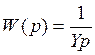 и переходная
и переходная ![]()
Найдем
весовую функцию 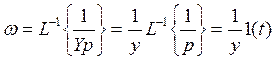
Представим графически
![]()
![]()
![]()
![]() M(t)
M(t)
![]()
![]()
![]()
![]()
![]() t
t
3.Статистическая характеристика линейных звеньев
Это зависимость между установившимися весовой и динамической характеристиками:
![]() - статистическая
характеристика
- статистическая
характеристика
Для линейных звеньев такая характеристика будет иметь вид линейных звеньев
![]()
![]()
![]()
 к
– коэффициент передача,
к
– коэффициент передача,
коэффициент усиления
![]()
![]()

![]()
![]()
Пользуясь теоремой о конечном значении, свяжем переходную функцию с к
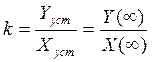
можем связать с к
![]()
перейдем к изображению Лапаласа
![]()
![]()
![]() - теореме о
конечном значении
- теореме о
конечном значении ![]()
![]()
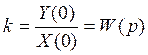
![]()
4.Частотные характеристики звеньев.
Важное значение при описании линейных стационарных систем (звеньев) имеют частотные характеристики. Они получаются при рассмотрении вынужденных движений системы при подаче на ее вход гармонического воздействия.
Предположим к звену приложено Sinое воздействие
 |
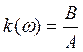 - коэффициент
передачи амплитуды, амплитудно-частотная характеристика (АЧХ)
- коэффициент
передачи амплитуды, амплитудно-частотная характеристика (АЧХ)
![]() - фазовый сдвиг, фазо-частотная характеристика
(ФЧХ)
- фазовый сдвиг, фазо-частотная характеристика
(ФЧХ) ![]() -безразмерное
время
-безразмерное
время
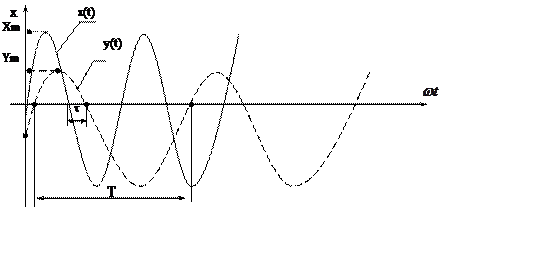 |
Эксперимент по прохождению гармонического сигнала предоставляет нам 2 характеристики: АЧХ и ФЧХ
Удобно ввести комплексно-значную
частотную характеристику ![]() , которая
содержала бы в себе всю информацию об объекте, т.е. объединила АЧХ и ФЧХ
, которая
содержала бы в себе всю информацию об объекте, т.е. объединила АЧХ и ФЧХ
![]()
![]() - частотная характеристика (ЧХ)
- частотная характеристика (ЧХ)
Для введения ЧХ на входе будет обобщенный гармонический сигнал
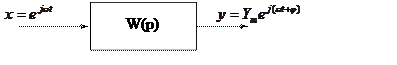 |
X = ejwt =1 - обобщенный гармонический сигнал, комплексное число интегрируемое как вектор, проекции которого дают обычные тригонометрические функции времени.
![]()
![]()
![]() -
переменная частота
-
переменная частота
Рассмотрим прохождение гармонического сигнала через линейное звено, описываемое уравнением (*).
На выходе будет сигнал
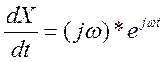
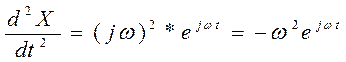
……………………………………………
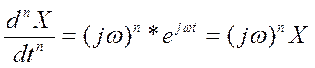
Также будут выражаться производные для выходного сигнала
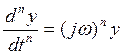
Определим частотой характерной Ф(jw) отношение общего выходного сигнала Y к общему входному сигналу.
Ф(jw) º ![]() в соответствии со (*)=
в соответствии со (*)=
=
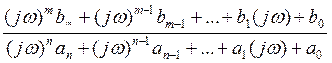 , видимо, что Ф(jw) = W(p) при условии, Р заменим на jw.
, видимо, что Ф(jw) = W(p) при условии, Р заменим на jw.
 |
Ф(jw) = W(p)|p ® tw
Частотная характеристика является частотно – зависимым комплексным числом, где w - круговая частота составляющих обобщенного гармонического сигнала.
Установим связь АЧХ, ФЧХ с ЧХ, для этого представим комплексное число
![]()
![]() +j
+j
![]()

![]() - вещественная частотная
характеристика (ВЧХ)
- вещественная частотная
характеристика (ВЧХ) ![]()
![]() - мнимая (МЧХ)
- мнимая (МЧХ) ![]()
![]() Тогда можно утверждать
Тогда можно утверждать ![]()
![]()
![]()
![]()
![]() +1
+1
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.