Основы теории автоматического управления. Основные термины и определения, страница 21

	Правая часть

 

Переходим к оригиналу:

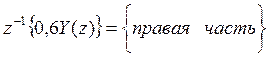
  алгоритм расчета переходного процесса

Рекуррентное (возвратное) уравнение. На данном шаге мы используем ранее вычисленное значение.

Составим расчетную таблицу

Рассмотрим

      

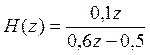
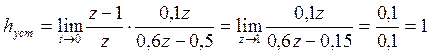
Построим график переходной функции

 

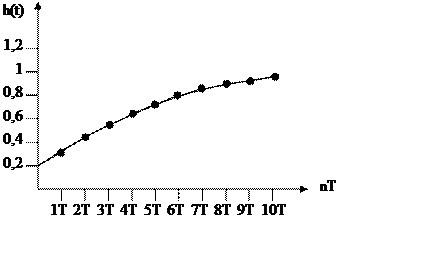8.7 Синтез цифровых регуляторов путем аппроксимации непрерывных передаточных функций.

Идея синтеза: синтезируется непрерывный вариант регулятора, который затем переводится в цифровую форму.

 

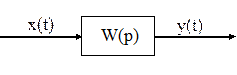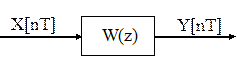Нужно найти:

           

Покажем, что

а)

 это можно делать если использовать уравнение из 8.4

б)

 

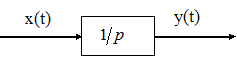В дискретном варианте:

 

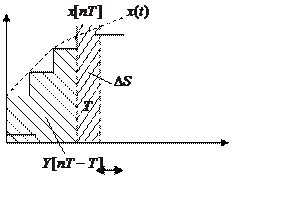Перейдем от оригиналов к изображениям

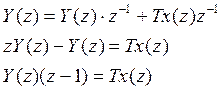
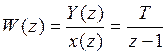 дискретная передаточная функция интегратора в цифровой форме

В качестве уточнения можно полагать, что приложения надо рассчитывать как площадь трапеции.

Это рассмотренный метод аппроксимации по методу прямоугольника.

Более точный метод трапеции

 - рассчитывается по двум значениям.

 

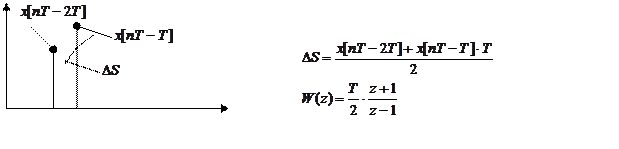8.8 Обобщение метода аппроксимации непрерывных регуляторов произвольной сложности.

1) Основан на разложении параметра z в ряд Маклорена

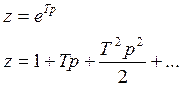
Заменим:

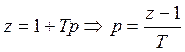
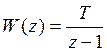
2)  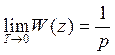                    метод прямоугольника для интегратора

                 

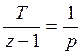
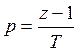
3) Основан на замене используя аппроксимацию по методу трапеции.

             

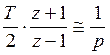
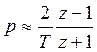
Процедура получения дискретной передаточной функции сводится к замене через  одним из трех способов.

Нам дан аналоговый регулятор

 

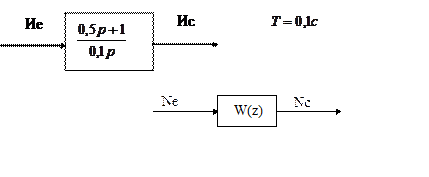Требуется найти

Используем для аппроксимации метод прямоугольника

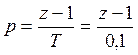
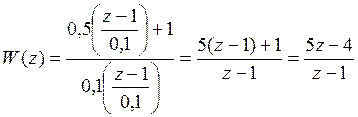
Найдем алгоритм цифрового регулятора от передаточной функции

           

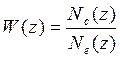
Переходим к оригиналам

Используя различные аппроксимации  мы будем получать различные дискретные передаточные функции, которые в пределе будут давать одни и те же передаточные функции.

8.9 Постановка задачи анализа цифровых аналитических систем ЦСАУ (цифровые системы)

8.9.1. Функциональные схемы ЦСАУ

Одноконтурная ЦСАУ

 

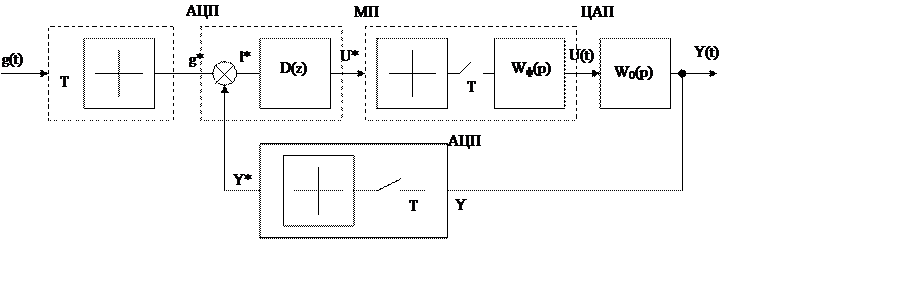
АЦП – аналогово-цифровой преобразователь, на входе непрерывный сигнал на выходе код

g(t) – задание

y – выходная координата

D(z) дискретная передаточная функция определяет алгоритм обработки сигнала рассогласования ε

y* - вых. код процессора

ЦАП – цифро-аналоговый преобразователь

- экстраполятор фиксирующий вых напряжение U(t) на период Т

Передаточная функция нулевого порядка

 - перед. функция непрерывной части системы

8.9.2 Структурные схемы ЦСАУ

Одноконтурная ЦСАУ

 

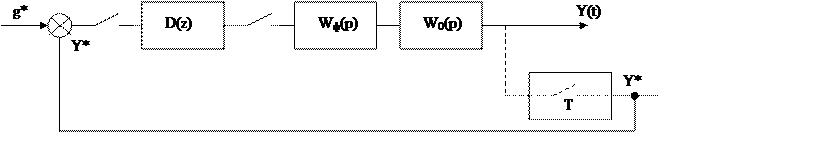Дополнительные фиктивные квантоват. по времени (ключ), импульсный модулятор – формирователь y* по непрерывному сигналу Y(t)

Введем дискретную передаточную функцию

Дискретная передаточная функция объекта

Передаточная дискретная функция разомкнутой системы (без обратной связи)

 - последовательное соединение звеньев

Справедливы все формулы непрерывных систем

Для параллельного соединения

 

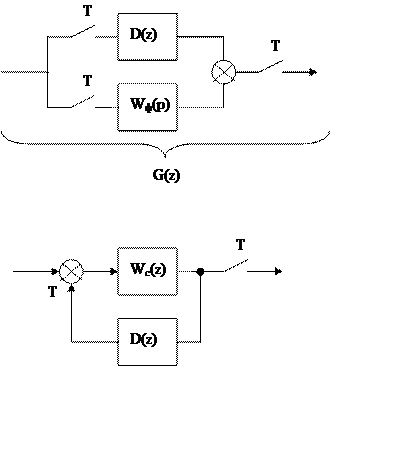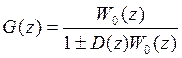
 дискретная передаточная функция замкнутой системы

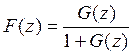
8.10 Анализ устойчивости ЦСАУ

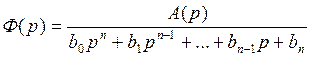
Корни полинома знаменателя определяют устойчивость системы

 - характеристическое уравнение

              корни

            

Если все корни имеют отрицательную часть, то система устойчива. Если если - положительную то не устойчива

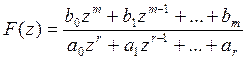
Переф. критерий устойчивости с учетом этой связи

Установим соответствие между точкой p-плоскости и точкой z-плоскости

 - действительная часть  - мнимая

                                                                

 

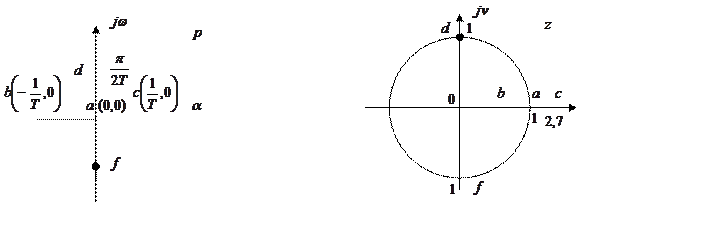
Точка
a	0	0	1	0
b		0		0
c		0		0
d	0		0	1
f	0		0	-1

Точки мнимой оси р отображения в единичной окружности плоскости z. Точки левой полуплоскости р отображаются внутрь единичного круга, точки правой – находятся вне единичного круга.

Общий критерий устойчивости: система устойчива если полоса передаточной функции замкнутой системы находятся внутри единичной окружности

              

            

Если выполняется для всех корней то система устойчива

Если =1 то система на грани устойчивости

Знак строгого равенства – граница устойчивости.

8.11 Выбор периода квантования Т.

Теорема Котельникова: для того чтобы импульсно модулируемый сигнал , содержащий частоты до  (ширина спектра) можно было восстановить в непрерывный сигнал, необходимо чтобы период квантования Т удовлетворял.

Приемлемое качество работы системы. «Стробоскопический эффект»