Учебно-справочное руководство по статистическим расчетам в изучении курса "Математическая статистика", страница 4

3. Используя метод “условного нуля”, определить числовые характеристики выборок по каждому признаку: выборочное среднее; выборочную дисперсию; исправленную выборочную дисперсию; исправленное выборочное среднее квадратическое отклонение. Дать объяснение полученным результатам.

4. Для каждого признака построить 99% или 95% доверительные интервалы для оценки генеральных средних, генеральных средних квадратических отклонений. Дать объяснение полученным результатам.

5. При уровне значимости a=0,05 или a=0,1 проверить гипотезы о нормальных законах распределения генеральных совокупностей по каждому признаку.

6. Для признаков X и Y построить корреляционное поле, эмпирическую ломанную регрессии и дать предварительный анализ зависимости между признаками.

7. Для признаков X и Y вычислить эмпирический коэффициент детерминации и эмпирическое корреляционное отношение.

8.  Определить параметры уравнения линейной регрессии.

9. Определить коэффициент корреляции и проверить его на значимость. Сделать вывод о наличии линейной связи между признаками.

10. Составить нелинейное уравнение регрессии, выбрав подходящий тип нелинейности.

11. Построить полученные линии регрессии в одной системе координат.

12. Для всех моделей рассчитать теоретический коэффициент детерминации и теоретическое корреляционное отношение; среднюю квадратическую погрешность уравнения; среднюю относительную погрешность аппроксимации.

13. Используя лучшее из полученных уравнений регрессии дать точечный прогноз  значения У при мощности пласта X = 1,8м .

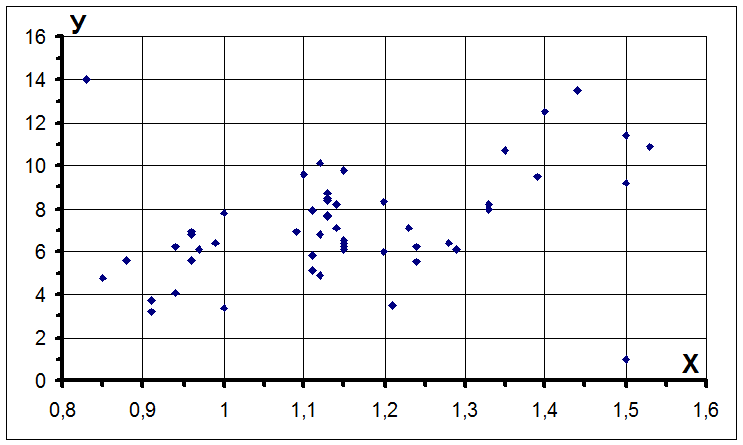
Решение задачи начнем с проверки исходных данных. Построим корреляционное поле, в котором будут представлены 52 точки (объем выборки  n = 52).

 

Из построенной диаграммы видим, что две точки (0,83; 14) и (1,5; 1) “выскакивают” из общей совокупности. Анализ исходных данных с позиции возможности большой  производительности (у=14 т/вых) при малой мощности пласта   (х = 0,83 м) и малой производительности (у=1 т/вых) при большой мощности пласта (х=1,5 м) позволяет отнести эти точки к ошибочным и исключить их из дальнейшего рассмотрения. Следовательно, объем выборки на этом этапе принимается n = 50.

Продолжим решение задачи.

а) Для признака Х  определим наибольшее и наименьшее значение признака:   X_min=0,85 ;   X_max=1,53  ;     

Число интервалов разбиения определим по формуле Стэрджесса:

k =1 + 3,322× lg n =  1 + 3,322× lg 50 = 6,6 » 7.

Найдем шаг разбиения  h = (Х_max – X_min) / k.

В данном случае  h = (1,53 – 0,85) / 7 = 0,097. Примем  h  = 0,1.

Произведем группировку данных для признака Х. Для этого подсчитаем, сколько значений признака Х  попадет в каждый из интервалов разбиения. Причем, при совпадении значения признака с одной из границ интервала, включаем это значение в  левый   интервал. Результаты группировки заносим в табл.2.  В третьем столбце таблицы заносятся штриховые отметки. Это удобный прием подсчета частот. Начинают с первого элемента выборки. В нашем случае он равен 1,13. Затем находят интервал (1,05 – 1,15), в который это наблюдение попадает, и ставят в третьем столбце штриховую отметку. Остальные наблюдения обрабатывают аналогично в том порядке, в котором они представлены в начальной выборке.

Если пользователь может использовать табличный процессор Excel, то после ввода  признака Х можно данные рассортировать в порядке возрастания, и тогда штриховые отметки не понадобятся.

б)  Для признака У  определим наибольшее и наименьшее значение признака:  у_min=3,2 ;       у_max=13,5  Число интервалов разбиения определим по формуле Стэрджесса:

k =1 + 3,322× lg n =  1 + 3,322× lg 50 = 7

Найдем шаг разбиения  h = (y_max – y_min) / k.

В данном случае  h = (13,5 – 3,2) / 7 = 1,471. Примем  h  = 1,48.

Произведем группировку данных для признака У. Результаты группировки заносим в табл.3

Таблица 2  Обработка признака Х

№	Интервалы	Штриховая отметка	Частоты   ni	Середина интервала хi	Частости	Ордината гистогр.	Накопленные частоты	Ордината кумуляты
1	0,85 - 0,95	IIIIII	6	0,9	0,12	1,2	6	0,12
2	0,95 -1,05	IIIIIII	7	1	0,14	1,4	13	0,26
3	1,05 -1,15	IIIIIIIIIIIIIIIIIIII	20	1,1	0,4	4	33	0,66
4	1,15 -1,25	IIIIII	6	1,2	0,12	1,2	39	0,78
5	1,25 -1,35	IIIII	5	1,3	0,1	1	44	0,88
6	1,35 -1,45	III	3	1,4	0,06	0,6	47	0,94
7	1,45 -1,55	III	3	1,5	0,06	0,6	50	1
S			50		1	10

Таблица 3    Обработка признака У

№	Интервалы	Штриховая  отметка	Частоты   ni	Середина интервала yi	Частости	Ордината гистогр.	Накопленные частоты	Ордината кумуляты
1	3,2 - 4,68	IIIII	5	3,94	0,1	0,068	5	0,1
2	4,68 - 6,16	IIIIIIIIIIII	12	5,42	0,24	0,162	17	0,34
3	6,16 - 7,64	IIIIIIIIIIIIII	14	6,9	0,28	0,189	31	0,62
4	7,64 - 9,12	IIIIIIIIII	10	8,38	0,2	0,135	41	0,82
5	9,12 - 10,6	IIII	4	9,86	0,08	0,054	45	0,9
6	10,6 -12,08	III	3	11,34	0,06	0,041	48	0,96
7	12,08-13,56	II	2	12,82	0,04	0,027	50	1
S			50		1	0,676