Учебно-справочное руководство по статистическим расчетам в изучении курса "Математическая статистика", страница 12

Условный нуль : С=600.

Проверка: 74 = 122 + 2·(–44) + 40  –  верно.

Из таблицы находим условные моменты:

М₁ =  -44/40 = –1,1;   М₂ = 122/40 = 3,05.

Выборочная средняя равна:

 =М₁·h +C =  380.

Выборочная дисперсия равна:

D_в = [M₂  - (M₁)²]·h²  =  73600          

Выборочное среднее квадратическое отклонение равно

271,2932 .

S ² =  ;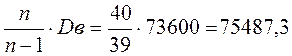

 .

Полученные результаты позволяют сделать следующие выводы.

Среднее время безотказной работы путевого стопора по выборке равно 380 час. Средний разброс времени безотказной работы путевого стопора вокруг среднего  по выборке равен 274,749 час.

Проверим гипотезу о показательном законе распределения распределении признака Х.  Используем критерий Колмогорова –Смирнова.

Показательный закон распределения является однопараметрическим распределением с параметром l.  Оценим параметр l с помощью характеристик выборки  следующим образом

l   .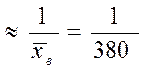

Для каждого интервала признака Х необходимо вычислить вероятности попадания признака  в данный интервал. Используем готовую формулу из теории вероятности для величины, имеющей показательное распределение:

.

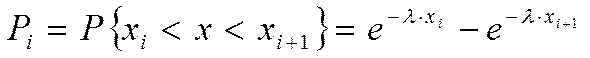Далее  заполним таблицу, причем крайнюю левую точку интервала заменяем на 0 ; крайнюю правую точку заменяем на + ¥, поскольку теоретическое показательное распределение определено для положительных значений аргумента.

Теоретические частоты найдем по формуле:

 ,       n=40 .

Находим накопленные частоты: для эмпирических частот – n×F_n(x) ; для теоретических частот – n×F(x).  Для этого следует для каждого интервала последовательно складываем частоты, начиная с первого интервала и заканчивая текущим интервалом. Затем вычисляем модуль разности накопленных частот в каждом интервале ôn×F_n(x) – n×F(x)ô = n×ôF_n(x) – ×F(x)ô. Заполним таблицу.

X i	X i+1	n i	Pi	n×Pi	n×Fn(x)	n×F(x)	ôn×Fn(x)–n×F(x)ô
100	300	24	0.55	21.84	24.00	21.84	2.16
300	500	6	0.19	7.43	30.00	29.27	0.73
500	700	4	0.11	4.39	34.00	33.66	0.34
700	900	3	0.06	2.59	37.00	36.25	0.75
900	1100	2	0.04	1.53	39.00	37.79	1.21
1100	1300	1	0.06	2.21	40.00	40.00	0.00
Итого		40	1.00	40.00

Из последнего столбца таблицы находят наибольшее из полученных модулей

  n ×D = max{n×ôF_n(x) – ×F(x)ô} = 2,16.

Определяем наблюдаемое значение критерия согласия Колмогорова

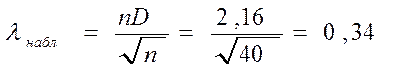                       .                              Этот критерий является случайной величиной, которая подчиняется закону распределения  Колмогорова.

По таблице критических точек (приложение 8), используя заданный уровень значимости a = 0,2  находят критическое значение критерия

         l_кр =  l(0,2) = 1,07.

Сравниваем: l_набл < l_кр, значит, нет оснований отвергнуть нулевую гипотезу H₀. Следовательно, гипотезу о  показательном законе  распределения времени безотказной работы стопора можно считать правдоподобной.

5 Элементы корреляционного и регрессионного анализа

          Зависимость между переменными случайными величинами Х и У, при которой каждому значению одной из них соответствует определенное среднее значение другой величины, называется корреляционной.  Функция, описывающая такую зависимость, называется регрессией. По виду функции  различают  линейную и нелинейную регрессии, по количеству зависимых переменных –  одномерную и множественную регрессии. Признак Х, соответствующий независимой переменной, будем называть факторным, признак У, соответствующий зависимой переменной, будем называть результативным.

5.1 Корреляционное поле

Пусть статистические данные представляют собой ряд пар связанных значений числовых признаков Х и У:

 (х₁ ;y₁),  (х₂ ;y₂), ..., (х_i ;y_i), …, (х_n ;y_n)  .  

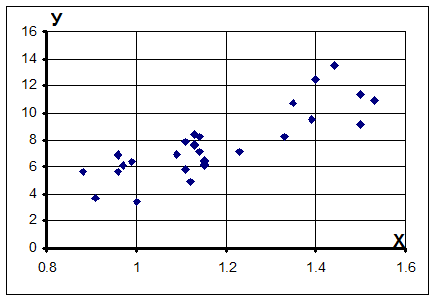Корреляционное поле – это графическое представление статистических данных в прямоугольной системе координат ХОУ, где каждой паре на плоскости соответствует точка. Построенное корреляционное поле позволяет на начальном этапе исследования сделать предварительный вывод как о наличии зависимости между признаками Х и У, так о виде этой зависимости.

5.2 Эмпирическая ломаная регрессии

          Эмпирическая ломаная регрессии строится по точка,  где  х_j – середины интервалов разбиения признака Х;  – средние групповые значения признака У в каждом интервале признака Х:   = (Σ y_i)/n_j . Здесь суммирование ведется только по тем значениям y_i , для которых значение х_i попало в j-тый интервал; n_j – берется из интервального статистического ряда  признака Х для j-го интервала.

5.3 Эмпирический коэффициент детерминации и эмпирическое корреляционное отношение

          Для измерения тесноты связи между признаками Х и У применяются эмпирический коэффициент детерминации и эмпирическое корреляционное отношение.

          Эмпирический коэффициент детерминации находится по формуле:

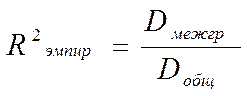 , где D_межгр – межгрупповая дисперсия результативного признака У; D_общ – общая дисперсия результативного признака У ( можно использовать выборочную дисперсию признака У, найденную при одномерном анализе).

Можно также дисперсии определять по формулам:

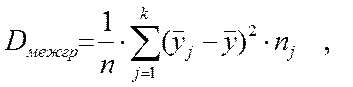                                                   (1)

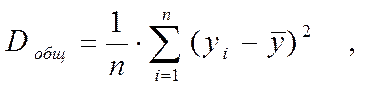                                             (2)

где k – число групп по факторному признаку Х;

n – объем выборки;

y_i – индивидуальные значения результативного признака У;

– его средние групповые значения;

 – среднее значение признака У;

n_j – частота в j – той группе (берется из статистического рядя признака Х).

          Эмпирическое корреляционное отношение равно корню квадратному из коэффициента детерминации

                

5.4 Линейная регрессия