Расчет неразрезных балок, страница 7

(i = 1,...,n)

Для получения формул, позволяющих определять поперечные силы в неразрезной балке, воспользуемся дифференциальной зависимостью

Q= dM

dx

Тогда с учетом (10.27) и (10.28) формулы для определения поперечных сил имеют вид в случае действия нагрузки

и в случае действия осадки опор

Q=

li

X i  - X i -1

li

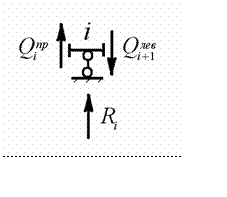
Опорные реакции неразрезной балки согласно рис. 10.20

Рис.10.20

определяются по формуле

R= Qлев+ Qпр

i             i +1              i

где     лев

(i = 0,1,...,n)

Qi +1  - поперечная сила в крайнем левом сечении пролета, примыкающе-

Qпр-  поперечная сила в крайнем правом сечении проле-

та, примыкающего слева к опоре

10.2.8.Алгоритмрасчетанеразрезнойбалки

Для заданной неразрезной балки:

1.При   наличии   защемляющих   опор   произвести   их   эквивалентное стержневое изображение.

2.Выполнить нумерацию опор и пролетов, начиная счет первых с 0 и счет вторых с 1.

3.Составить  уравнение  трех  моментов  для  каждой  промежуточной опоры.

4.Решить систему уравнений трех моментов и найти значения опорных моментов в сечениях промежуточных опор.

5.Определить  для  каждого  пролета  в  характерных  сечениях  значения изгибающих моментов и поперечных сил и построить их эпюры.

6.По найденным значениям поперечных сил в соответствующих сечениях, примыкающих к опорам, определить опорные реакции.

7.Выполнить  окончательные  статические  и  кинематические  поверки метода сил.

10.3. Расчет неразрезных балок на действие неподвижной нагрузки с использованием фокальных свойств

10.3.1.Фокальныесвойстванеразрезной балки

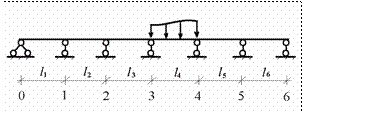
Рассмотрим  неразрезную  балку,  загруженную  неподвижной  нагрузкой в одном пролете (рис.10.21)

Рис. 10.21

При  таком  нагружении  схеме  деформирования  очертанию  изогнутой  оси неразрезной балки присуща определенная закономерность. Она заключается  в  чередовании  направления  прогибов  в  незагруженных  пролетах.  Поскольку  очертание  изогнутой  оси  неразрезной  балки  связано  с  изгибаю- щими  моментами  выясним,  какие  в  этом  случае  возникают  закономерно- сти распределения изгибающих моментов в незагруженных пролетах.

Запишем первое уравнение трех моментов, связанное с первой промежуточной опорой

~

(10.29)

Свободный член в уравнении (10.29) отсутствует, так как к первой проме- жуточной  опоре  примыкают  два  незагруженных  пролета.  Из  (10.29)  най- дем соотношение опорных моментов

~  ~

X1                        l2

(10.30)

Из (10.30) следует, что опорные моменты во втором незагруженном пролете имеют разные знаки. Их отношение является некоторой постоян- ной величиной k2, которая зависит только от геометрических и жесткост- ных параметров балки и не зависит от нагрузки. Модуль этого отношения не может быть менее 2.

Запишем второе уравнение трех моментов, связанное со второй промежуточной опорой

l2 X1

+ 2(~

+ ~)X

~

(10.31)

Свободный  член  в  уравнении  (10.31) отсутствует,  так  как  и  к  этой  опоре примыкают  два  незагруженных  пролета.  Из  (10.31)  найдем  отношение опорных моментов. С учетом ранее полученного  соотношения (10.30) оно имеет вид