Решение алгебраических и трансцендентных уравнений. Метод сеток решения уравнений параболического типа, страница 9

 Кубическим сплайном, соответствующим данной функции  и узлам , является функция , удовлетворяющая следующим условиям:

а) на каждом из отрезков  (i = 0, 1, 2,…, n) функция   является многочленом третьей степени вида

 i = 0, 1, 2,…, n-1;               (26)

б)  непрерывны на [a, b];

в) должно выполняться условие интерполяции, т. е.

, i = 0, 1, 2,…, n-1.                                                   (27)

Так как на каждом из n отрезков  между узлами сетки сплайн  определяется четырьмя коэффициентами , то для его полного построения необходимо найти 4n чисел.

Найдем первую, вторую и третью производные многочлена :

,                                                   (28)

,                                                                      (29)

.                                                                                     

Для любой точки  из (26), (28), (29) получим

.

Согласно условию интерполяции (27) будем иметь

, .                                                    (30)

, i = 0, 1, 2,…, n-1.                                                      

.                     (31)

Шаг разбиения интервала [a, b] (шаг сетки) , ()

Тогда (31) запишем в виде

.

Так как , то

.                                               (32)

Согласно условию б) (условие непрерывности) в каждом узле  левая и правая производные  должны быть равны, т. е. не должно быть точек разрыва и должны выполняться условия

,                                                                   (33)

.                                                                 (34)

.

.

Тогда

,  i = 0, 1, 2,…, n-2.                                     (35)

Используя (34), получим

.

.

,  i = 0, 1, 2,…, n-2.                                         (36)

Полученные соотношения представляют собой алгебраическую систему для определения (4n-2) коэффициентов. Недостающие два уравнения получают из граничных условий. В общем случае рассматривают три вида граничных условий, которым должен удовлетворять сплайн :

1)  или ;

2)  или ;

3) .

Условия 1), 2) применяют, если известны значения соответствующих производных функции  на концах отрезка [a, b]. Условия вида 3) называют периодическими и их выполнения требуют, если функция  периодическая с периодом (b-a).

Для концевых узлов  полагаем  (что соответствует нулевой кривизне графика на концах рассматриваемого отрезка). Тогда используя условия (11), получим

.                                                       (37)

Заметим, что условие  совпадает с (36) при , если положить .

Из (36) получим

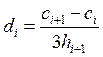.                                                                             (38)

После подстановки  и  в (31) получим выражение для :

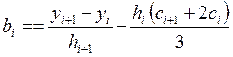.                                                   (39)

Далее подставим  и  в (35) (и уменьшим значение индекса i на единицу для симметрии записи) и приходим к уравнениям:

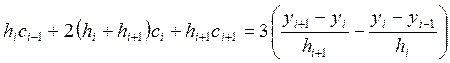 i = 1, 2,…, n-1.                               (40)

Система (40) вместе с условиями , образует систему для определения коэффициентов .  Матрица этой системы трехдиагональная, и система легко решается методом прогонки. Другие коэффициенты сплайна вычисляются по формулам (30), (38) и (39).

___________________________________________________________________________

3.1. Построить интерполяционный многочлен вида по следующим данным:

f(-2) = - 50, f(-1) = - 22,  f(0) = - 8,  f(1) = - 2,  f(2) =  26.

3.2. Построить интерполяционный многочлен вида  для функции  по ее значениям в точках x₀ = -1, x₁ = 0, x₂ = 1, x₃ = 2, x₄ = 3 и вычислить

f (-0,5).

3.3. Найти интерполяционные многочлены Лагранжа для следующих функций, заданных таблицами: