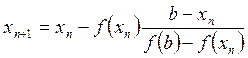 . (4)
. (4)
Пример.
Методом хорд
найти корни уравнения ![]() .
.
Построив
график функции ![]() , находим, что данное уравнение
имеет один действительный корень, лежащий в интервале [1,4; 1,5].
, находим, что данное уравнение
имеет один действительный корень, лежащий в интервале [1,4; 1,5].
Проверим
условие нахождения корня в данном интервале ![]() <
0.
<
0.
f(1,4) = - 0,05788 < 0,
f(1,5) = 0,21640 > 0.
![]() <0, следовательно, условие
нахождения корня в найденном интервале выполняется.
<0, следовательно, условие
нахождения корня в найденном интервале выполняется.
Далее найдем 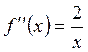 .
.
![]() = 1,42857 > 0,
= 1,42857 > 0,
![]() = 1,33333 > 0.
= 1,33333 > 0.
Определим
неподвижную точку согласно условию![]() >
0. Так как
>
0. Так как ![]() > 0, то точка
> 0, то точка ![]() =
1,5 является неподвижной, а в качестве начального приближения корня выбираем
точку
=
1,5 является неподвижной, а в качестве начального приближения корня выбираем
точку ![]() = 1,4.
= 1,4.
Каждое (n + 1) приближение корня
вычисляем по формуле 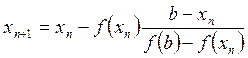 .
.
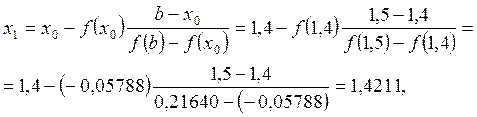
 = 1,42152,
= 1,42152,
![]() = 1,42153,
= 1,42153,
![]() = 1,42153.
= 1,42153.
Сравнивая ![]() и
и ![]() , видим, что корнем уравнения является
число
, видим, что корнем уравнения является
число ![]() = 1,42153.
= 1,42153.
Метод итерации (метод последовательных приближений)
Метод итерации является универсальным: его можно применять для решения обширного класса как линейных, так и нелинейных уравнений. Сущность этого метода заключается в следующем. Пусть дано уравнение
![]() , (5)
, (5)
где ![]() -
непрерывная функция, и требуется найти его вещественные корни. Преобразуем
уравнение (5) в эквивалентное уравнение вида
-
непрерывная функция, и требуется найти его вещественные корни. Преобразуем
уравнение (5) в эквивалентное уравнение вида
![]() . (6)
. (6)
Выберем начальное приближение x0
и, подставив его в правую часть уравнения (6), получим число ![]() . Затем вычислим
. Затем вычислим ![]() и
т. д. Получим последовательность чисел
и
т. д. Получим последовательность чисел ![]() ,
определяемую равенством
,
определяемую равенством
![]() , n = 0, 1,
2,... (7)
, n = 0, 1,
2,... (7)
Для того, чтобы последовательность ![]() сходилась к корню с уравнения (5),
необходимо выполнение условия сходимости: если функция
сходилась к корню с уравнения (5),
необходимо выполнение условия сходимости: если функция ![]() определена и дифференцируема на отрезке [a,
b] и
определена и дифференцируема на отрезке [a,
b] и ![]() £q<1 при всех a < x < b, то процесс итерации
£q<1 при всех a < x < b, то процесс итерации ![]() , n = 0, 1, 2,... сходится к корню с уравнения
, n = 0, 1, 2,... сходится к корню с уравнения ![]() независимо от начального значения
независимо от начального значения ![]() .
.
Условие сходимости метода итерации
![]() £q <1, (8)
£q <1, (8)
где q
– максимальное значение производной ![]() на
интервале, в котором находится корень уравнения (если корней несколько,
то условие сходимости должно выполняться для каждого интервала).
на
интервале, в котором находится корень уравнения (если корней несколько,
то условие сходимости должно выполняться для каждого интервала).
Чем ближе к нулю максимальное значение производной q, тем выше скорость сходимости метода.
Замечание. Пусть в некоторой окрестности [a,
b] корня с уравнения ![]() производная
производная ![]() сохраняет постоянный знак и выполнено
неравенство
сохраняет постоянный знак и выполнено
неравенство ![]() £q<1. Тогда, если
производная
£q<1. Тогда, если
производная ![]() положительна, т. е. 0£
положительна, т. е. 0£![]() £q<1,
то последовательные приближения
£q<1,
то последовательные приближения ![]() , n
= 0, 1, 2,...,
, n
= 0, 1, 2,..., ![]() сходятся к корню монотонно.
Если же производная
сходятся к корню монотонно.
Если же производная ![]() отрицательна, т.е. -1<-q£
отрицательна, т.е. -1<-q£![]() £0 то последовательные приближения колеблются около корня с.
£0 то последовательные приближения колеблются около корня с.
Для метода итерации большое значение имеет способ
преобразования уравнения (5) к виду (6), т. е. выбор функции ![]() , которая должна подчиняться условию
сходимости
, которая должна подчиняться условию
сходимости ![]() £ q <1.
£ q <1.
Рассмотрим один достаточно общий прием приведения уравнения (5) к виду (6), для которого обеспечено выполнение неравенства (8).
Пусть искомый корень лежит в интервале [a, b], причем
0 < m £
![]() £
M,
(9)
£
M,
(9)
для ![]() , где m
– наименьшее значение производной
, где m
– наименьшее значение производной ![]() на [a, b], а M – наибольшее значение производной
на [a, b], а M – наибольшее значение производной ![]() на [a, b].
на [a, b].
Если производная ![]() отрицательна,
то вместо уравнения
отрицательна,
то вместо уравнения ![]() рассматриваем уравнение
рассматриваем уравнение ![]() .
.
Заменим уравнение (5) эквивалентным уравнением вида
![]() , l
>0. (10)
, l
>0. (10)
Сравнивая (10) и (6), видим, что ![]() .
.
Так как метод итерации должен быть сходящимся и для
функции ![]() должно выполняться условие (8), то будем
иметь
должно выполняться условие (8), то будем
иметь
0 £ ![]() =
= ![]() £ q < 1. (11)
£ q < 1. (11)
Учитывая выражение (9), получим следующую оценку:
0 £ ![]() £
£
![]() £
q. (12)
£
q. (12)
Можно положить:
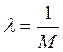 (13)
(13)
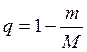 < 1. (14)
< 1. (14)
В методе итерации в качестве начального приближения ![]() чаще всего принимается один из концов
интервала [a, b].
чаще всего принимается один из концов
интервала [a, b].
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.