Решение алгебраических и трансцендентных уравнений. Метод сеток решения уравнений параболического типа, страница 7

Как для произвольно заданных узлов интерполирования, так и для равномерно отстоящих узлов применяется интерполяционная формула Лагранжа:

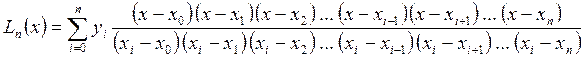.                 (6)

При  (линейная интерполяция) формула (6) представляет собой уравнение прямой , проходящей через две заданные точки :

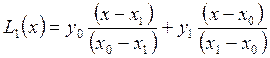.                                                        (7)

При  (квадратичная интерполяция) формула (6) представляет собой уравнение параболы , проходящей через три заданные точки :

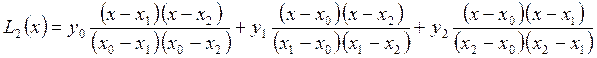.               (8)

Разность  называется погрешностью интерполяции или остаточным членом интерполяции.

В узлах интерполяции погрешность = 0, в остальных точках она отлична от нуля.

Если  имеет непрерывную  производную, то возможно представление остаточного члена интерполяции в виде

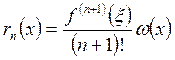,                                                               (9)

где  зависит от x и лежит внутри отрезка [a, b] (а = x₀ < x₁ < ... < x_n = b).

.

Формула (9) справедлива для всех точек отрезка [a, b], в том числе и для узлов интерполирования.

Принимая , получим оценку погрешности интерполяции в текущей точке :

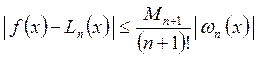.                                                           (10)

Оценка максимальной погрешности интерполяции на всем отрезке [a, b]:

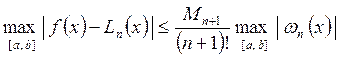.                                          (11)

Пример 1.

Построить интерполяционный полином Лагранжа для функции  на 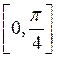, если  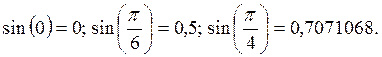С помощью интерполяционной формулы вычислить 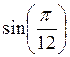 и оценить погрешность.

Имеем три узла интерполяции 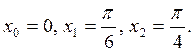 Так как , то строим полином второй степени .

Воспользуемся формулой (8).

 =

= .

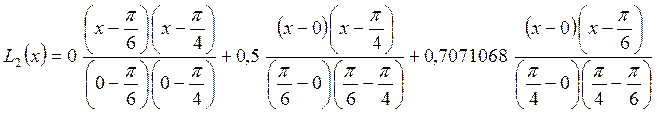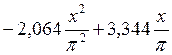Погрешность интерполяции оценим, используя формулу (10):

.

.

.

.

.

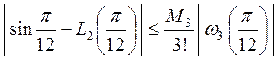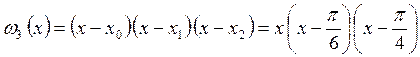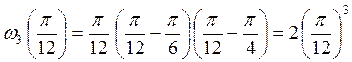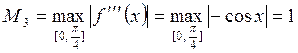Получим следующую оценку

.

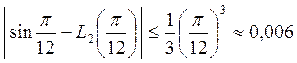Используя полученный интерполяционный полином , вычислим :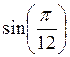

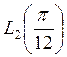= 0,264333.

Таким образом, .

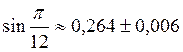(Точное значение ).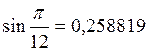

Пример 2.

Дана таблица значений

Найти значение .

Чтобы найти значение в любой промежуточной точке необходимо построить интерполяционный полином по табличным данным. Построим полином Лагранжа

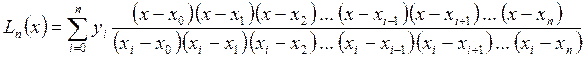
для n = 3 (i = 0,1,…, n).

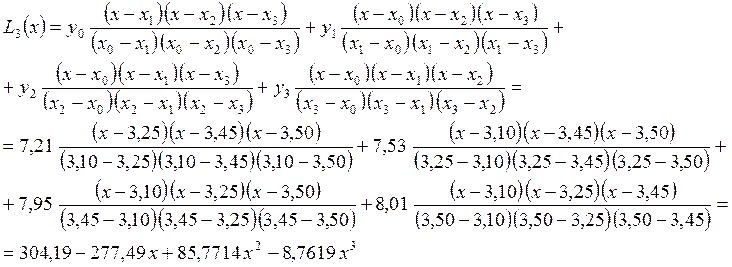
Итак, интерполяционный полином Лагранжа для заданных табличных данных имеет следующий вид .

Так как при интерполяции значение  в каждом узле  совпадает со значением , то, для нахождения значения  используем полученный полином Лагранжа, т. е.

Аппроксимация функций. Метод наименьших квадратов

Интерполяционный полином не всегда удобен для приближения функций. Если таблица значений содержит результаты какого-то эксперимента, полученные с погрешностью, то не целесообразно проводить кривую точно через все узлы, как при интерполяции. На практике часто используют другой способ приближенного представления (аппроксимации) функций, заданных таблицей, который называется методом наименьших квадратов.

Пусть функция  задана таблицей приближенных значений , . Согласно методу наименьших квадратов за меру отклонения полинома

                                                        (12)

от данной функции  на множестве точек  принимают величину

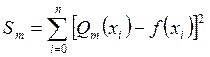,                                                                 (13)

равную сумме квадратов отклонений полинома  от функции  на заданной системе точек. Очевидно, что  - это функция коэффициентов . Эти коэффициенты нужно подобрать так, чтобы величина  была наименьшей. Полученный полином называется аппроксимирующим для данной функции, а процесс построения этого полинома – точечной квадратичной аппроксимацией функции.

Для нахождения коэффициентов  найдем частные производные от величины

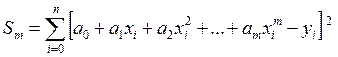,                                          (14)

где , по всем переменным . Приравнивая эти частные производные нулю, получим систему  уравнений с  неизвестными:

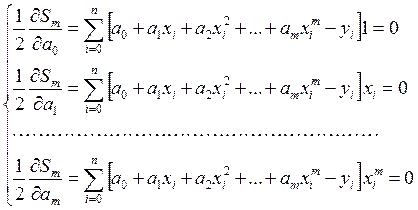.                          (15)

В общем случае, когда аппроксимирующий полином для данной функции является обобщенным: , где  - функции, находим частные производные от величины 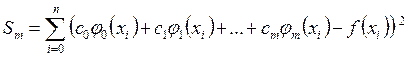. Согласно (15), будем иметь систему уравнений, позволяющую определить коэффициенты ,

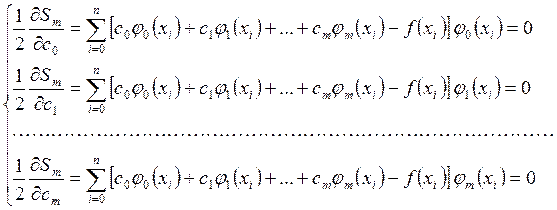.           (16)