Решение алгебраических и трансцендентных уравнений. Метод сеток решения уравнений параболического типа, страница 6

где матрица  имеет вид .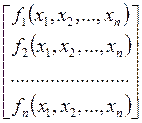

Пусть система (11) приведена к виду:

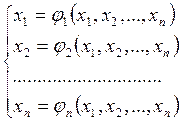,                                                              (13)

или в матричной форме

,                                                                    (14)

где матрица  имеет вид .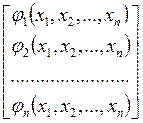

Каждое последующее (n+1) приближение можно вычислить по итерационной формуле

, (n = 1, 2, ...)                                                  (15)

Условие сходимости: процесс итерации (15) сходится к единственному решению системы (14), если выполняется одно из условий

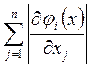£ q_i < 1, (i = 1, 2, …, n) или 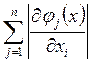£ q_i < 1, (i = 1, 2, …, n).

Начальное приближение 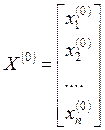 выбирают произвольно из области сходимости метода итерации.

Процесс итерации может быть применен также к общей системе нелинейных уравнений (12). Перепишем эту систему в виде

,                                                                      (16)

где L - неособенная матрица (определитель этой матрицы не равен нулю).

Сравнивая (14) и (16), видим, что

.                                                                 (17)

Если  имеет непрерывную производную 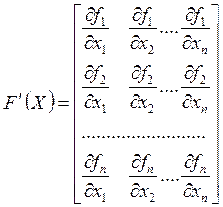 в некоторой

окрестности изолированного решения системы (11), то, учитывая (17), получим

.

Учитывая условие сходимости процесса итерации, матрицу L выбираем таким образом, чтобы . Отсюда, если матрица  неособенная, то будем иметь . Учитывая все это, получим итерационную формулу для нахождения корней системы (1)

.                                                     (18)

Замечание: в случае, если , то следует выбрать другое начальное приближение .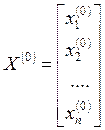

Пример.

Методом итерации решить систему нелинейных уравнений

.

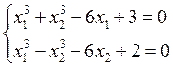В матричном виде заданная система уравнений имеет вид , где

.

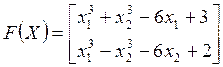Итерационная формула, по которой можно найти корни данной нелинейной системы, имеет следующий вид

.

В качестве начального приближения возьмем матрицу .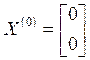

Тогда 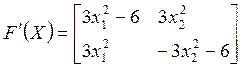; ; 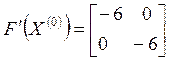= 36.

Если определитель матрицы  = 0, то необходимо выбрать другое начальное приближение .

;          .

;

.

.

; ; ; ; .

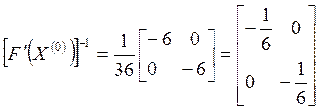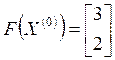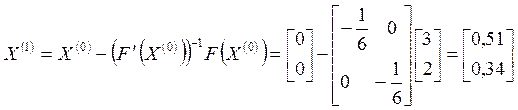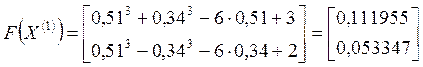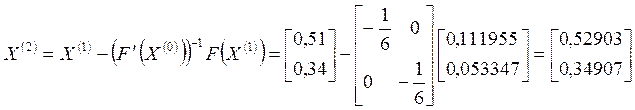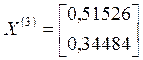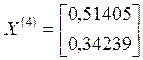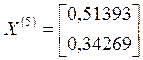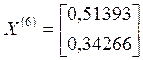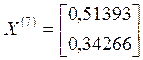Итак, решением данной системы нелинейных уравнений является матрица .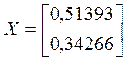

______________________________________________________________________________

Найти решения следующих линейных систем:

2.1.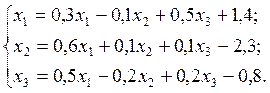              

2.2.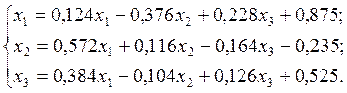

2.3.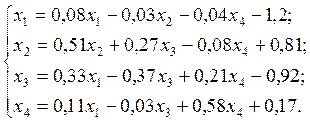

2.4.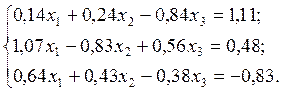

2.5.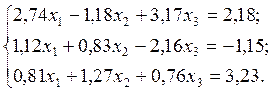

2.6.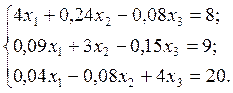

2.7.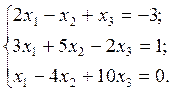

2.8.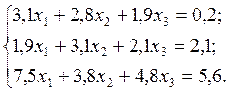

2.9.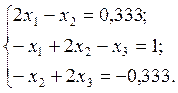

2.10.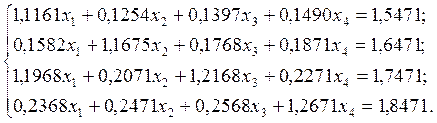

Найти решения нелинейных систем:

2.11. 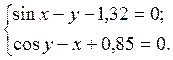                   2.15.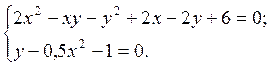

2.12. 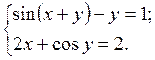                       2.16.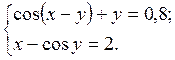                

2.13. 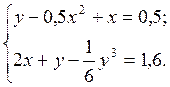                    2.17.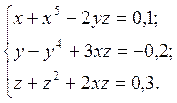

2.14.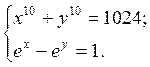            

3. Приближение функций

Интерполирование функций

Пусть в точках а = x₀ < x₁ < ... <x_n = b, называемых узлами интерполяции, функция  задана таблицей своих значений

.                                                 (1)

Задача интерполирования заключается в том, чтобы построить функцию  (интерполирующая функция), принадлежащую известному классу и принимающую в узлах интерполяции те же значения, что и , т. е. такую, что

.                                                   (2)

Геометрически это означает, что нужно провести кривую  некоторого определенного типа, проходящую через систему заданных точек.

Линейную комбинацию

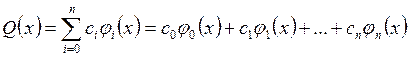                             (3)

с действительными коэффициентами  называют обобщенным многочленом (полиномом) по системе функций , i = 0, 1, …, n.

На практике чаще всего используются следующие системы:

1)  - алгебраическая интерполяция;

2)  - тригонометрическая интерполяция (применяется для приближения периодических функций);

3) , где - некоторая числовая последовательность попарно различных действительных чисел, - экспоненциальная интерполяция.

Рассмотрим интерполирование функции  полином  степени не выше n, удовлетворяющим условию (2), т. е. таким, что

.                                                    (4)

Такой полином называется интерполяционным. Как известно, существует единственный полином вида  степени не выше n, принимающий в точках  заданные значения. Коэффициенты а_i полинома можно определить из системы уравнений

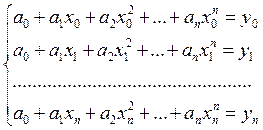,                                                         (5)

где . Определителем этой системы является определитель Вандермонда

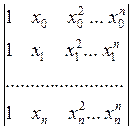 ¹ 0.

Он отличен от нуля при всяких различных между собой , и интерполяционный многочлен существует и он единственный.