В реальном
механизме ![]() . С учетом этого замечания (1) примет вид.
. С учетом этого замечания (1) примет вид.
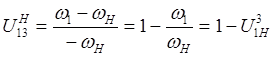 (2)
(2)
Из (2) найдем
![]()
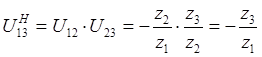 при неподвижном водиле – послед-ое сод.
зубчатых колес.
при неподвижном водиле – послед-ое сод.
зубчатых колес.
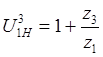
Кинематика дифференцированных зубчатых механизмов.
 Дифференцированным
называется механизм, который имеет один вход и несколько выходов.
Дифференцированным
называется механизм, который имеет один вход и несколько выходов.
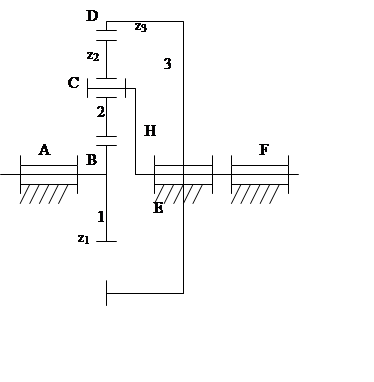
W = 3n – 2p1 – p2
n=4
p1 =4 (A, C, E, F)
p2 =2 (B, D)
![]() (установим
зависимость)
(установим
зависимость)
1. Рисуем кинематическую схему и проводим ее структурный анализ.
2. Создаем обращенный механизм, для чего каждому звену мысленно сообщаем угловую скорость – ωн, при этом водило останется неподвижным.
3. Находим передаточное отношение обращенного механизма.
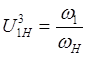 (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
![]()
Подставим (2) и (3) в (1).
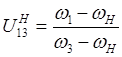
![]()
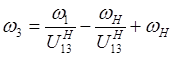 (4)
(4)
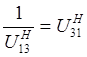 , так как
, так как 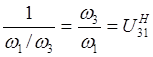 (5)
(5)
С учетом (5), (4) примет вид
![]() (6)
(6)
![]()
![]()
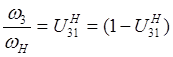 (7)
(7)
![]()
![]()
![]()
Кинематика замкнутых зубчатых дифференцированных механизмов.
Если в зубчатом дифференциале связать дополнительной (смыкающей) передачей два к.- л. звена, имеющих неподвижные оси вращения, то получится механизм с 1-ой степенью свободы, который получил название замкнутого дифференцированного зубчатого механизма.
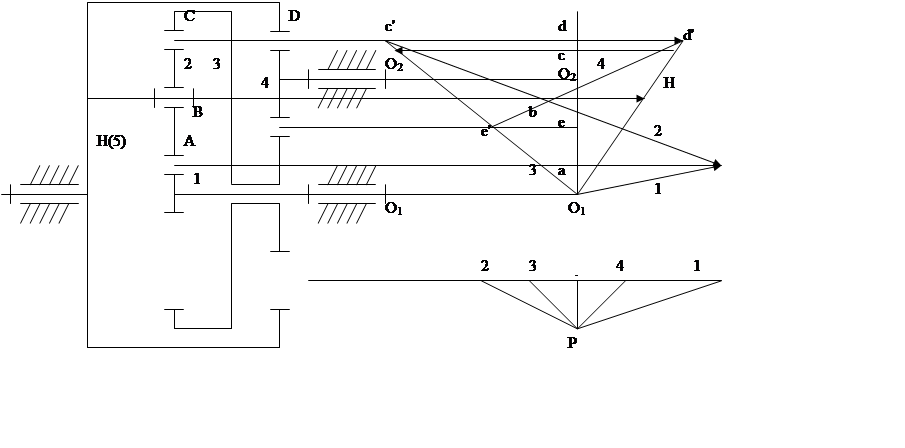 Аналитическое
определение
Аналитическое
определение
![]()
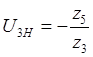 ,
, 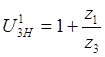 ,
, 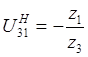
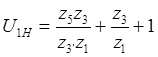
Синтез структурных групп с помощью математической модели.
![]()
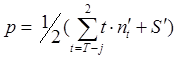
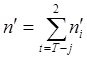
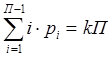
![]()
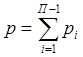
n' – число звеньев, входящих в группу Ассура
S' – число внешних кинематических пар структурных групп
Пример: Найдем
структурную группу при следующих условиях П=3, ![]()
![]()
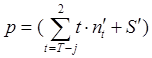
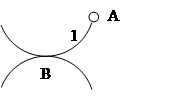
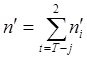
![]()
![]()
![]()
Система имеет
решение, если ![]() , тогда р=2, а n' =1/
, тогда р=2, а n' =1/
Практически реализовать получившиеся параметры можно только при линейном звене Т=2, значит решением системы будет n2 =1 и S'=2.
А – низшая одноподвижная кинематическая пара.
В – высшая двухподвижная кинематическая пара.
Подвижность кулачковых механизмов.
Кулачковые механизмы находят широкое применение в технике, благодаря простоте изготовления и эксплуатации. Формируя соответствующий профиль кулачка, можно получить практически любой закон движения его выходного звена.
Обычно подвижность кулачковых механизмов определяется формально, т. е. высшую кинематическую пару считают двухподвижной, сам механизм относят к плоскому, который, как подразумевается, существует в 3-хподвижном пространстве. Поэтому определение подвижности ведут по формуле Чебышева.
Такой подход не соответствует действительности и поэтому не верен. Рассмотрим примеры.
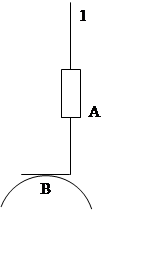
Пример 1. Плоский кулачковый механизм с точечным контактом в высшей кинематической паре.
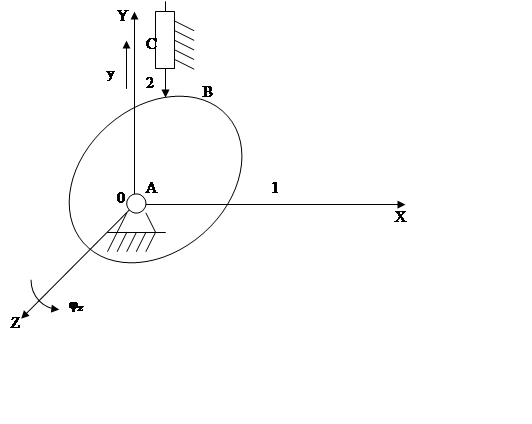 1 – кулачок
1 – кулачок
В – высшая кинематическая пара
С – вращающаяся одноподвижная пара
2 – толкатель
Механизм преобразует вращательное движение кулачка 1 в поступательное толкателя 2.
В исследованиях механизмов имеется2 простейших перемещения
(П=2) – одно вращательное вокруг оси Z и одно поступательное вдоль оси Y.
W
= Пn - 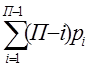
![]() , для исследуемых механизмов
, для исследуемых механизмов ![]()
или W = 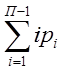 - kП, где
- kП, где ![]()
![]()
Пример 2. Плоский кулачковый механизм с плоским толкателем.
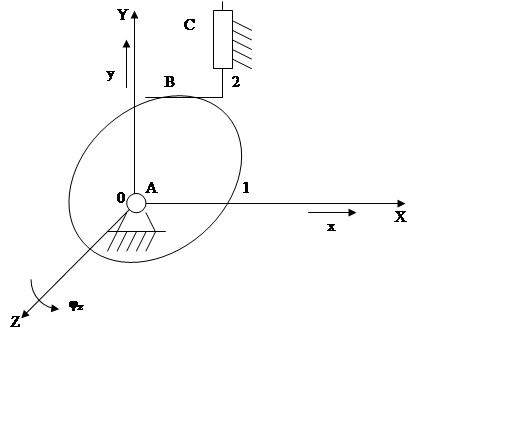
1 – кулачок
2 – толкатель
А – вращающая кинематическая пара
С - поступательная
кинематическая пара
В – высшая (двухподвижная, сложн. движ., которое можно разложить на движения вдоль X и Y.
П = 3, n = 2, p1 = 2, p2 = 1
или, для W
= 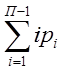 -
kП,
-
kП, ![]()
![]()
Пример 3. Плоский кулачковый механизм с толкателем и роликом.
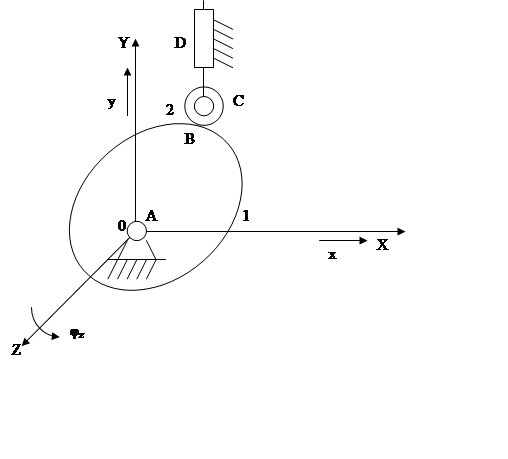
1 – кулачок
2 – ролик
3 – толкатель
П = 3, n = 2, p1 = 3 (A, C, D), p2 = 1(B)
W = 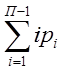 - kП,
- kП, ![]()
![]()
Пример 4. Плоский кулачковый механизм с коромыслом и роликом.
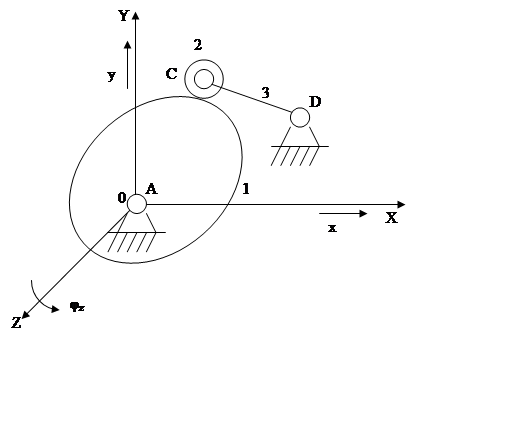
1 – кулачок
2 – ролик
3 – коромысло
П = 3 (φz, x, y)
n = 3, p1 = 3, p2 = 1
W = 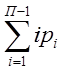 - kП,
- kП, ![]()
![]()
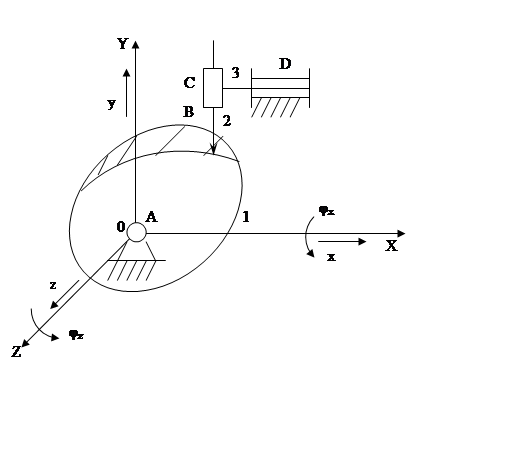 Пример 5. Объемный кулачковый
механизм с точечным контактом в высшей кинематической паре.
Пример 5. Объемный кулачковый
механизм с точечным контактом в высшей кинематической паре.
1 - кулачок
2 – толкатель
3 – звено
П = 4 (φх, φzx, y)
p1 = 3(A, C, D), p2 = 1(В)
W = 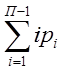 -
kП,
-
kП, ![]()
![]()
Пример 6. Объемный кулачковый механизм с плоским толкателем.
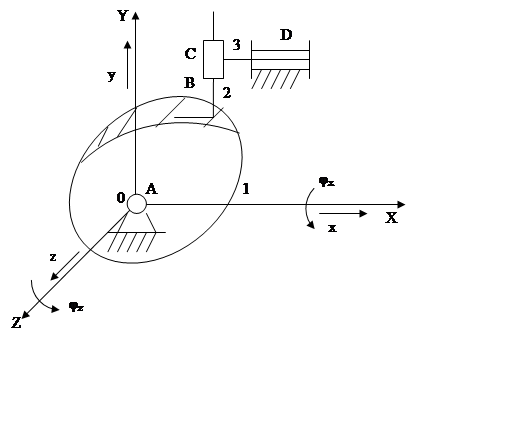
1 - кулачок
2 – толкатель
3 – звено
n = 3, П = 5 (φх, φzx, y, z)
p1 = 3(A, C, D), p3 = 1(В)
W = 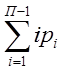 -
kП,
-
kП, ![]()
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.