Задачи, приводящие к появлению понятия иррационального числа. Разработка материалов для учебного модуля, страница 16

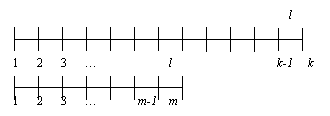
kl    =   k  

ml        m

 

…

Слово «соизмеримые» используется для описания двух длин, отношение которых есть рациональное число.»

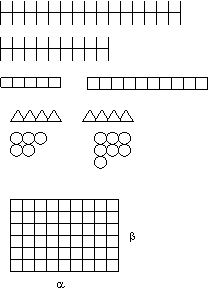
Задание 6. Найти общую меру величин a и b 

1.

2.

3.

4.

5.

Учитель: Давайте кто-нибудь к доске, будем вместе исткать общую меру для этих двух отрезков.

Ученик: (задание 6.1) отрезок a=9, b=15. Накладываем а на b, остается остаток 6, накладываем 6 на отрезок а, остается 3. Этим отрезоком можно измерить и отрезок a и отрезок b. Значит общая мера 3.

Учитель: теперь запиши все, что ты сказал, предлагаю обозначать получающиеся остатки r₁, r₂, r₃, …

Ученик: Значит так: a=15, b=9.

а= b+6, 6-это r₁, значит а= b + r₁   

b= r₁ + r₂,  r₂=3

r₁ = 2r₂  остаток r₃=0.

Учитель: Хорошо, следующие задания выполняете самостоятельно, если появляются вопросы – задавайте.

…

Ученик: а в последнем задании общую меру чего искать?…а понятно, сторон.

Обсуждение как выполняли задания, и какие были трудности. Решение

последнего выносится на доску.

…

Объяснение учителя: тот способ, которым вы искали общую меру в последнем задании, называется процедура последовательного взаимного отнятия квадратов (процедура антифайресиса). Этот метод можно использовать и для нахождения общей меры отрезков, если разместить отрезки так, чтобы они были сторонами прямоугольника. Эта процедура была описана Евклидом и поэтому может быть вам известна под названием алгоритм Евклида.

Работа с текстом [28]. «Процедура антифайресиса (алгоритм Евклида).

Наибольшая общая мера двух величин a и b  (b<a) может быть найдена с помощью процедуры антифайресиса («последовательное взаимное отнятие»), известной под названием алгоритм Евклида.

Будем отнимать b от a до тех пор, пока не получится остаток n<b. При этом искомая наибольшая мера a и b  будет также наибольшей общей мерой b и  n. Будем теперь отнимать n от b до тех пор, пока не получится остаток d<n. При этом искомая наибольшая мера b и n будет также наибольшей мерой n и d. Будем повторять описанный процесс последовательного взаимного отнятия до тех пор, пока на каком-нибудь шаге «мерка» не уложится в «вымеряемом» нацело. Эта последняя «мерка» и будет наибольшей общей мерой исходных величин a и b.  Идея процедуры антифайресиса может быть наглядно представлена на схеме «отнятия квадратов».

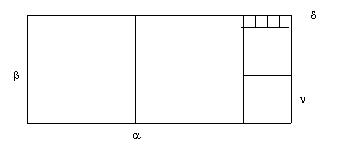
От прямоугольника a´b отнимаются квадраты b´b. От остатка b´g отнимаются квадраты g´g. От остатка g´d отнимаются квадраты d´d. И так до тех пор, пока на очередном шаге квадраты не заполнят соответствующий прямоугольник нацело. Если это произойдет, сторона последнего квадрата w´w будет служить наибольшей общей мерой отрезков a и b.

 

a=n₀b+n, b=n₁n+d, n=n₂d+e, n=n₃e+z, …

(числа n_0, n_1, n_2, n_3,…называют подходящими частными). Данным соотношениям может быть придан такой вид (если первое равенство разделить на b, второе на n, третье на d, и так далее):

 ,    ,    ,   ,……