Числовые характеристики случайных величин, страница 6

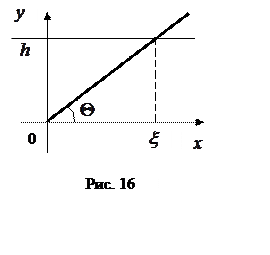
Как уже отмечалось, для распределения Коши характерно отсутствие моментов, т.к. интеграл 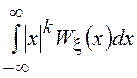 расходится при любых значениях =1,2,…

Характеристическая функция распределения Коши равна

=.

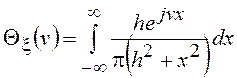Найдем ПВ суммы = 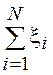независимых СВ , каждая из которых подчиняется распределению Коши с параметром . Пользуясь методом ХФ, получим , что 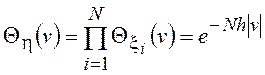, а ПВ 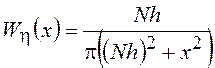, т.е. мы получили распределение Коши с параметром .

Полученный результат определяет устойчивость распределения Коши. В этой связи дадим определение [2].

Распределение с ХФ  называется устойчивым, если для любых ,  найдутся , >0 такие, что .

Наш случай соответствует =0 и =+. Это определение можно сформулировать и в терминах ПВ. Сделать это предлагается читателю.

3.5.5.4. Гамма-распределение.

Случайная величина  имеет гамма-распределение с параметрами (>0, >0), если

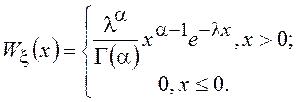
Функция распределения равна нулю при , а при  выражается через неполную гамма-функцию (см. главу 6)

.

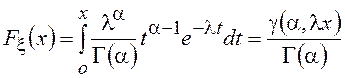Характеристическая функция имеет вид

.

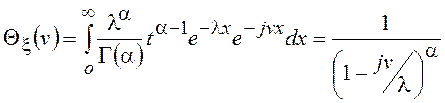Этот результат при целых  можно получить без вычисления интеграла с помощью следующих рассуждений. При =2,3,…, гамма-распределение дает ПВ суммы независимых СВ  , подчиненных показательному (экспоненциальному) распределению

,

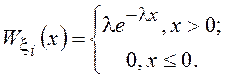имеющему ХФ 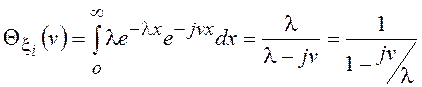. Учитывая свойство ХФ суммы независимых СВ, получим

.

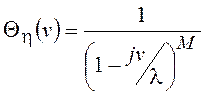Гамма-распределение при =1,2,3,… называется распределением Эрланга и играет важную роль в теории массового обслуживания и теории надежности. При = и  оно дает ПВ длительности интервала времени до появления  событий (вызовов, отказов) процесса Пуассона с параметром . Определение процесса Пуассона будет дано далее в разделах, посвященных случайным процессам.

Начальные моменты  равны 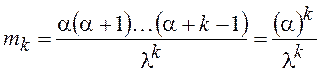, а дисперсия, асимметрия и коэффициент эксцесса определяются следующими выражениями: , , .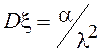

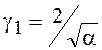При = и = гамма-распределение превращается в -распределение с  степенями свободы, играющем важную роль в задачах математической статистики. С ним мы познакомимся позже.

3.5.5.5. Распределение Лапласа.

Плотность вероятности распределения Лапласа, или двойного экспоненциального распределения, имеет вид

=, .

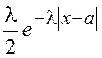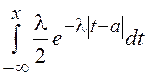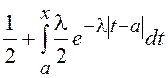Функция распределения может быть записана как = при  и = при  или окончательно

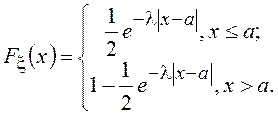
С помощью несложных вычислений можно найти ХФ для распределения Лапласа

=,

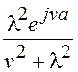начальные моменты

,

,

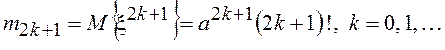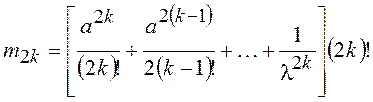дисперсию 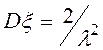, асимметрию  и эксцесс .

3.5.5.6. Бета-распределение.

Плотность вероятности случайной величины , принимающей значения на интервале  и имеющей бета-распределение с параметрами >0, >0, может быть записана как

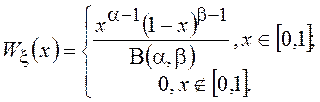
Функция распределения выражается через неполную бета-функцию

,

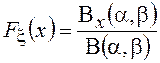см. главу 6 первой части пособия.

Начальные моменты 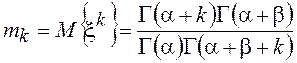, откуда для дисперсии , асимметрии  и коэффициент эксцесса  можно получить следующие выражения:

,

=,

=.

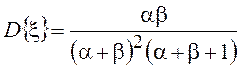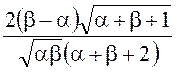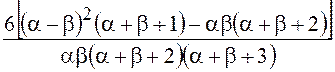Характеристическая функция представляется с помощью степенного ряда и здесь не приводится. При целочисленных значениях параметров = и = бета-распределение дает ПВ -ой порядковой статистики (-ого элемента в вариационном ряду ) , полученного путем упорядочивания (ранжирования) исходной выборки , состоящей из независимых и равномерно распределенных на интервале  СВ. При =1 и = мы имеем распределение наименьшего и наибольшего значений соответственно.

Для ФР наименьшего и наибольшего значений в выборке из  независимых СВ с ФР  будет иметь соответственно  и . Дифференцируя обе части, записанных равенств по , получим  и .

Читателю предлагается убедиться в этом. При ==1 бета-распределение совпадает с равномерным, а при == может быть сведено к закону арксинуса.

3.5.6. Распределения, связанные с нормальным.

С нормальным распределением мы сталкивались и знакомились на протяжении почти всего предшествующего материала второй части настоящего пособия. Фундаментальная роль нормального распределения определяется содержанием центральной предельной теоремы, простейший вариант которой (следствие из теоремы Линдеберга [1]) звучит так.

Если независимые случайные величины  одинаково распределены и имеют конечные отличные от нуля дисперсии, то при  равномерно по