Числовые характеристики случайных величин, страница 11

В результате этой операции мы получим нормальный случайный вектор с корреляционной матрицей  и вектором средних значений , где  и  – корреляционная матрица и вектор средних значений исходного случайного нормального вектора .

Важным и очень полезным свойством нормального n – мерного вектора является возможность выразить смешанный корреляционный момент вида 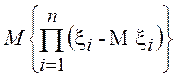 через ковариацию компонент вектора, т.е.  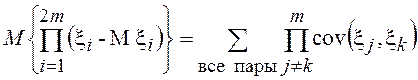и 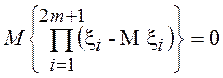. Число пар равно числу различных способов выбора пар из 2m различных элементов и как известно из комбинаторики, равно .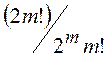

Например, для m = 2 имеется 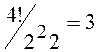 три способа разделения произведения 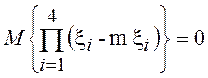 на произведение ковариаций, т.е.

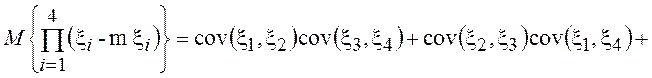
С помощью этой формулы можно найти ковариацию для квадратов нормальных СВ, положив  и .

Тогда

.

В ряде задач теории вероятностей и математической статистики приходится встречаться с многомерными аналогами рассмотренных выше одномерных распределений. Это распределение Дирихле, обобщающее бета – распределение, многомерное распределение Стьюдента и многомерный аналог  – распределения – распределение Уишарта. С указанными распределениями можно познакомиться с помощью [5].

Контрольные вопросы

1. Зачем для описания случайных величин вводятся числовые характеристики?

2. Дайте определение начальных  и центральных  моментов для непрерывных и дискретных СВ.

3. Что такое условное математическое ожидание? Что показывают кривой регрессии СВ  и .

4. Как связаны между собой начальные и центральные моменты СВ?

5. Назовите свойства математического ожидания и дисперсии.

6. Что характеризует асимметрия и коэффициент эксцесса?

7. Дайте определение -квантильи.

8. Что такое медиана, мода? Что называют наивероятнейшим значением СВ?

9. Дайте определение ковариация СВ  и .

10. Что такое коэффициент корреляции? В каких пределах он может меняться?

11. Найти коэффициент корреляции СВ = и =, где  - СВ с ПВ вида 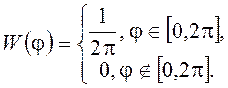. Объяснить результат.

12. Как определяются кумулянты? Что они характеризуют?

13. Для биномиального распределения с помощью ХФ найдите  и проверьте приведенные выражения для асимметрии биномиального распределения .

14. Определите , для геометрического распределения.

15. С помощью ХФ проверьте справедливость утверждения, что для распределения Пуассона с параметрами  математическое ожидание  и  дисперсия  равны .

16. Какие распределения, связанные с равномерным, вы знаете?

17. Постройте ФР для распределения Симпсона, приведенного на рис. 16. Найдите квартили  и . Определите интерквартильный размах и сравните его с СКО=.

18. Найдите ПВ случайных величин , если 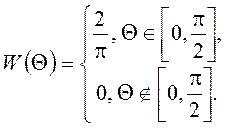. Вычислите  и .

19. Какие распределения называются устойчивыми? Как в терминах ПВ определяются устойчивые распределения?

20. Найдите квартили  и  для распределения Лапласа. Сравните интерквартильный размах с .

21. Найдите ПВ наибольшего и наименьшего значений в выборке из  независимых и равномерно распределенных на промежутке  СВ. Определите соответствующие найденным ПВ средние значения.

22. Какой будет кривая регрессии  на , если  и  образуют нормальный случайный вектор  с математическими ожиданиями , , и дисперсиями ,  соответственно и коэффициентом корреляции ?

23. Найдите ПВ разности двух нормальных СВ.

24. Построить эллипс с центром в точке , где  и  - средние значения совместно нормальных СВ  и  , вероятность попадания в который точки с координатами  и  равнялась бы 0,9. Считать ==4 и =0,5.

25. Какая СВ имеет распределение  с  степенями свободы?

26. Дайте определение понятия выборки из генеральной совокупности.

27. Опишите процедуру построения эмпирического распределения.

28. Что называется статистикой Пирсона? Каковы ее свойства?

29. Какому распределению подчиняется модуль и аргумент нормального случайного вектора , где  и  независимы и имеют математические ожидания ,  и одинаковые дисперсии ? Как изменятся распределения  и , если  ?

30. Вычислите для случая  математические ожидания модуля вектора, медиану и наивероятнейшее значение.

31. Сформулируйте важнейшие свойства многомерного нормального распределения.