Числовые характеристики случайных величин, страница 4

Заканчивая знакомство со случайными величинами, рассмотрим основные распределения, описывающие СВ, наиболее часто встречающиеся на практике.

3.5.1. Распределение Бернулли

Распределение Бернулли, введенное в начале первого раздела, пример 1, описывает дискретную СВ, принимающую значение 1 с вероятностью , и значение 0 с вероятностью . Плотность вероятности данной СВ имеет вид

.

Характеристическая функция

=.

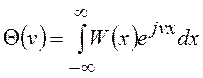Математическое ожидание и дисперсия равны соответственно

=, =-=-=.

3.5.2. Биномиальное распределение

Биномиальное распределение было достаточно подробно рассмотрено в примере 2 в начале раздела 1. Нам осталось определить только числовые характеристики и ХФ.

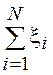Для решения этой задачи будем рассматривать результат (число успехов в серии из  последовательных испытаний) как сумму независимых СВ, подчиненных распределению Бернулли, т.е. принимающих значение 1 (успех в испытании) с вероятностью  и 0 (неудача) с вероятностью , т.е. СВ =, где  - независимые СВ, подчиненные распределению Бернулли.

Пользуясь правилами отыскания математического ожидания и дисперсии суммы (с учетом независимости СВ ), будем иметь:

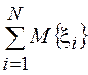== и ==().

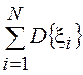Наивероятнейшее значение  находится в интервале . Учитывая независимость слагаемых, ХФ

.

Пользуясь приведенными выше соотношениями, нетрудно найти асимметрию распределения 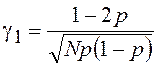 и коэффициент эксцесса 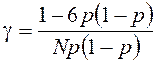. Видно, что с ростом  , что свидетельствует о справедливости локальной теоремы Муавра. Причем для величин  и  скорость сходимости к нормальному распределению в смысле, указанном в формулировке теоремы Муавра, зависит от величины , определяющей симметрию биномиального распределения. Скорость сходимости зависит от величины () и будет максимальна при . На практике, если  удовлетворяет условиям:

()>9 и ,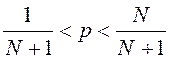

то для определения вероятности  можно пользоваться приближенными формулами вида

=.

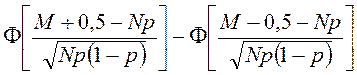Для ФР биномиальной СВ в этих условиях справедливо приближенное представление

,

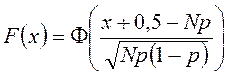причем если 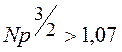, то ошибка при использовании нормального распределения вместе биномиального не превосходит 0,05 для всех . В приведенных формулах 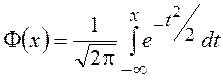 - подробно рассмотренный в главе 6 первой части пособия интеграл вероятностей.

3.5.3. Отрицательное биномиальное распределение (распределение Паскаля)

Случайная величина  описывается отрицательным биномиальным распределением с параметрами (,), если

, =0,1,2,…

При натуральном  это распределение дает вероятность того, что в схеме последовательных независимых испытаний с вероятностью успеха  до получения ровно  успехов пройдет  испытаний. При =1 данное распределение называют геометрическим. Числовые характеристики СВ , подчиненной отрицательному биномиальному распределению, имеют вид:

==; =; =; =.

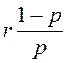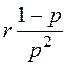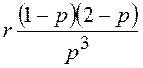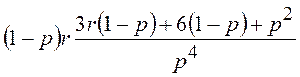В качестве упражнения читателю предлагается доказать справедливость формулы для  и  при =1.

3.5.4. Распределение Пуассона

К распределению Пуассона приходят, рассматривая схему последовательных независимых испытаний в условиях, когда вероятность успеха зависит от числа испытаний  и  при числе испытаний .

При этом в соответствии с теоремой Пуассона [1]:

,

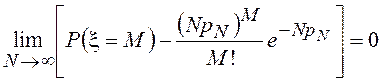иными словами, при  =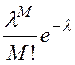, где = - параметр распределения Пуассона.

Рассмотрим конкретный пример, приводящий нас к распределению Пуассона. Пусть на телефонную станцию в случайные моменты времени поступают вызовы, относительно которых мы сделаем следующие предположения:

1. Вероятность поступления вызова в малый интервал  пропорциональна величине интервала , не зависит от положения интервала на оси времени и от того, поступил или нет вызов в предшествующем интервале.

2. Считается, что вероятность поступления двух и более вызовов в малый интервал  есть , т.е. бесконечно малая более высокого порядка, чем . Таким образом, в пределах промежутка времени  мы имеем = последовательных независимых испытаний с вероятностью успеха в одном испытании 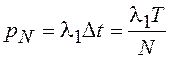. При сформулированных условиях мы имеем схему  последовательных независимых испытаний с вероятностью успеха в испытании 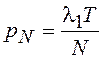, где  имеет смысл среднего числа успехов (вызовов) в единицу времени, а  - среднее число успехов за время . Тогда, в соответствии с теоремой Пуассона, вероятность того, что за время  интересующее нас событие (вызов) будет иметь место ровно  раз, равна