Глава 3. Числовые характеристики случайных величин
Рассмотренные выше функция распределения, плотность вероятности и характеристическая функция дают наиболее полное представление о СВ. Однако, являясь функцией одной или нескольких переменных, для многомерных СВ, они представляют собой достаточно сложные объекты. В многих случаях достаточно бывает использовать для описания СВ совокупность чисел, называемых числовыми характеристиками СВ. Познакомимся с этими числовыми характеристиками.
3.1. Моменты случайной величины
Под начальными моментами
СВ ![]() понимают величины
понимают величины 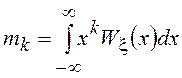 ,
среди которых особую роль играет
,
среди которых особую роль играет 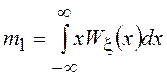 , называемый
математическим ожиданием или средним значением СВ
, называемый
математическим ожиданием или средним значением СВ ![]() . Моменты
СВ
. Моменты
СВ ![]() существуют тогда и только тогда, когда
существуют тогда и только тогда, когда 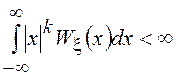 ,
, ![]() =1,2,…
Часто для записи математического ожидания используют символ статистического
усреднения, обозначаемый как
=1,2,…
Часто для записи математического ожидания используют символ статистического
усреднения, обозначаемый как ![]() ,
,![]() или
просто прямой чертой сверху, т.е.
или
просто прямой чертой сверху, т.е. ![]() ,
,![]() или
или
![]() . Для дискретных СВ, задаваемых распределением
(
. Для дискретных СВ, задаваемых распределением
(![]() ),
), ![]() =1,2,…,
=1,2,…,![]() , математическое ожидание равно
, математическое ожидание равно 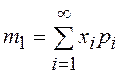 , если записанный ряд сходится абсолютно.
При использовании аппарата дельта-функций для дискретных СВ можно пользоваться
интегральной формой записи математического ожидания
, если записанный ряд сходится абсолютно.
При использовании аппарата дельта-функций для дискретных СВ можно пользоваться
интегральной формой записи математического ожидания
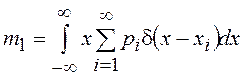 =
=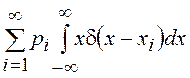 =
=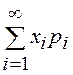 .
.
Математическое ожидание ![]() является точкой концентрации значений СВ в
том смысле, что среднеквадратический разброс значений СВ относительно
является точкой концентрации значений СВ в
том смысле, что среднеквадратический разброс значений СВ относительно ![]() минимален. Смысл понятия
среднеквадратический разброс будет уточнен ниже.
минимален. Смысл понятия
среднеквадратический разброс будет уточнен ниже.
 Являясь абсциссой центра тяжести
плоской фигуры, ограниченной осью абсцисс и кривой
Являясь абсциссой центра тяжести
плоской фигуры, ограниченной осью абсцисс и кривой ![]() ,
математическое ожидание характеризует положение ПВ относительно оси ординат.
Часто бывает полезно представление
,
математическое ожидание характеризует положение ПВ относительно оси ординат.
Часто бывает полезно представление ![]() с помощью ФР
с помощью ФР ![]() .
.
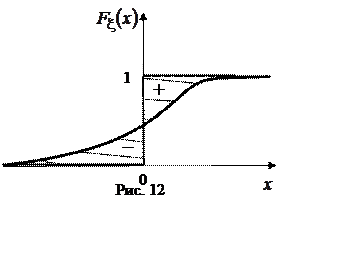
Можно показать [1,3,4,5],
что ![]() =
=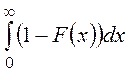 -
-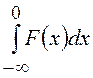 , т.е. математическое ожидание равно
разности площадей, заключенных между осью ординат, прямой
, т.е. математическое ожидание равно
разности площадей, заключенных между осью ординат, прямой ![]() =1 и кривой
=1 и кривой ![]() =
=![]() в интервале (
в интервале (![]() ) и
между осью абсцисс, кривой
) и
между осью абсцисс, кривой ![]() =
=![]() и
осью ординат в интервале (
и
осью ординат в интервале (![]() ). На рис. 12 указанные
площади заштрихованы и отмечен знак, с которым нужно взять соответствующие
площади.
). На рис. 12 указанные
площади заштрихованы и отмечен знак, с которым нужно взять соответствующие
площади.
Условное
математическое ожидание.Пусть дана условная ПВ ![]() .
Условным математическим ожиданием СВ
.
Условным математическим ожиданием СВ ![]() , относительно значения
, относительно значения ![]() СВ
СВ ![]() ,
относительно события {
,
относительно события {![]() =
=![]() },
называется выражение вида
},
называется выражение вида 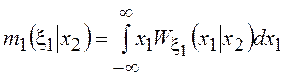 . Зависимость
. Зависимость ![]() от
от ![]() определяет кривую регрессии
определяет кривую регрессии ![]() на
на ![]() . При
этом переменную
. При
этом переменную ![]() , называют регрессионной переменной
или регрессором, а
, называют регрессионной переменной
или регрессором, а ![]() - откликом.
- откликом.
Математическое ожидание
может быть определено и для функций СВ ![]() , если
только существует интеграл
, если
только существует интеграл  , т.е.
, т.е. 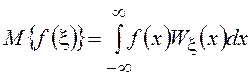 .
.
Для векторных и матричных
СВ (компоненты вектора и элементы матрицы есть СВ) математическое ожидание
определяется как вектор или матрица, в которых СВ заменены своими средними
значениями, т.е. ![]() , где
, где
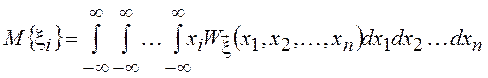 .
.
Аналогично определяется
математическое ожидание случайной матрицы. Читателю предлагается проверить
справедливость приведенной формулы для ![]() .
.
Наряду с начальными
моментами ![]() , для характеристики СВ используют
центральные моменты
, для характеристики СВ используют
центральные моменты ![]() =
=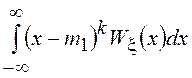 .
Важнейшим центральным моментом является
.
Важнейшим центральным моментом является ![]() ,
называемый дисперсией СВ
,
называемый дисперсией СВ ![]() и обозначаемый обычно
как
и обозначаемый обычно
как ![]() . Корень из дисперсии
. Корень из дисперсии ![]() называют среднеквадратическим отклонением
(значением) СВ
называют среднеквадратическим отклонением
(значением) СВ ![]() . В качестве упражнения рекомендуем
доказать, что если существует
. В качестве упражнения рекомендуем
доказать, что если существует ![]() , то
, то ![]() =0.
=0.
Теперь мы можем вернуться
к утверждению, что СВ имеет минимальный среднеквадратический разброс
относительно математического ожидания ![]() .
Запишем средний квадрат отклонения СВ
.
Запишем средний квадрат отклонения СВ ![]() от
некоторого значения
от
некоторого значения ![]()
![]() =
= . Раскрывая скобки и используя обозначения
начальных моментов, будем иметь
. Раскрывая скобки и используя обозначения
начальных моментов, будем иметь ![]() =
=![]() -2
-2![]()
![]() +
+![]() .
Исследуя данную функцию
.
Исследуя данную функцию ![]() на экстремум, получим
на экстремум, получим 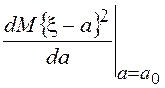 =0, откуда следует, что
=0, откуда следует, что ![]() =
=![]() . Вторая производная
. Вторая производная ![]() равна 2>0 и, следовательно,
равна 2>0 и, следовательно, ![]() =
=![]() соответствует минимуму
соответствует минимуму ![]() . Само минимальное значение
. Само минимальное значение ![]()
![]() =
=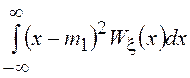 равно
дисперсии
равно
дисперсии ![]() .
.
Рассмотрим свойства математического ожидания и дисперсии.
1. Математическое ожидание постоянной (детерминированной величины) равно ей самой, а дисперсия равна нулю.
Так как для
детерминированной СВ ![]() , где
, где ![]() -
значение этой величины, то
-
значение этой величины, то 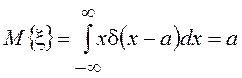 и
и 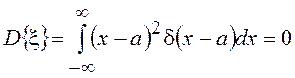 .
.
2. Математическое
ожидание суммы любых (зависимых и независимых) СВ равно сумме математических
ожиданий, т.к. ![]() =
=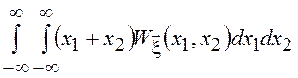 =
=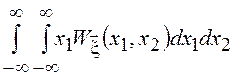 +
+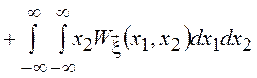 . Выполняя внутреннее
интегрирование в первом слагаемом по
. Выполняя внутреннее
интегрирование в первом слагаемом по ![]() , а во втором по
, а во втором по ![]() , получим
, получим
![]() =
=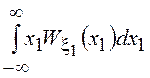 +
+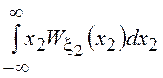 =
=![]() .
.
3. Постоянный множитель
можно выносить за знак математического ожидания, т.е. ![]() =
=![]() , т.к.
, т.к.
![]() =
=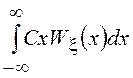 =
=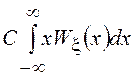 =
=![]() .
.
4. С учетом свойств 2 и 3
можно утверждать, что математическое ожидание линейной комбинации СВ 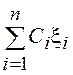 равно линейной комбинации с теми же
коэффициентами
равно линейной комбинации с теми же
коэффициентами ![]() математических ожиданий
математических ожиданий ![]() , т.е.
, т.е. 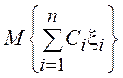 =
=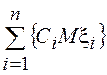 . Таким образом, для оператора
математического ожидания (статистического усреднения) справедлив принцип
суперпозиции, т.е. это – линейный оператор (функционал).
. Таким образом, для оператора
математического ожидания (статистического усреднения) справедлив принцип
суперпозиции, т.е. это – линейный оператор (функционал).
5. Математическое
ожидание произведения независимых СВ равно произведению их математических
ожиданий, т.е. ![]() =
=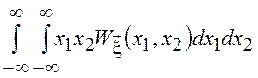 =
=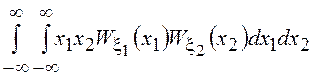 =
=![]() , т.к. переменные в
последнем двойном интеграле разделяются.
, т.к. переменные в
последнем двойном интеграле разделяются.
6. Дисперсия суммы или
разности независимых СВ равна сумме их дисперсий. Для суммы или разности
независимых СВ ![]() и
и ![]() дисперсия
равна
дисперсия
равна ![]() =
= ![]() =
=
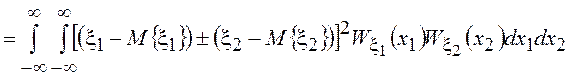 .
.
Возводя в квадрат и используя
введенные обозначения, будем иметь ![]() =
=![]() +
+![]() ±2
±2![]() =
=![]() +
+![]() ,
где
,
где ![]() - равные нулю первые центральные моменты СВ
- равные нулю первые центральные моменты СВ
![]() и
и ![]() .
Надеемся, что к этому времени читатель в этом убедился. Позже мы узнаем, что
для справедливости данного результата достаточно некоррелированности СВ
.
Надеемся, что к этому времени читатель в этом убедился. Позже мы узнаем, что
для справедливости данного результата достаточно некоррелированности СВ ![]() и
и ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.