![]() =
=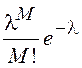 ,
, ![]() =0,1,2,…
=0,1,2,…
Это распределение и называется распределением Пуассона. Убедимся в том, что для записанного распределения выполняется условие нормировки
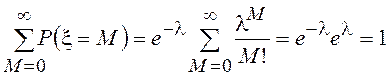 .
.
Характеристическая
функция для распределения Пуассона может быть найдена путем подстановки в ХФ
биномиального распределения 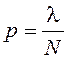 и предельного перехода
с учетом того, что
и предельного перехода
с учетом того, что 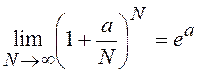 . В результате
. В результате
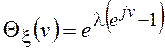 .
.
Математическое ожидание
СВ, описываемой распределением Пуассона, равно ![]() =
= 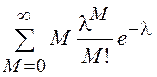 =
= 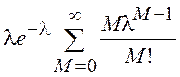 .
Учитывая, что
.
Учитывая, что 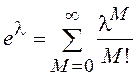 , ряд в выражении для
, ряд в выражении для ![]() есть
есть 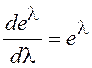 и
поэтому
и
поэтому ![]() =
=![]() . С помощью аналогичного
приема можно показать, что
. С помощью аналогичного
приема можно показать, что ![]() =
=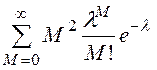 =
=![]() , и следовательно,
, и следовательно, ![]() =
=![]() -
-![]() =
=![]() ,
т.е. пуассоновская СВ имеет одинаковые математическое ожидание и дисперсию, равные
,
т.е. пуассоновская СВ имеет одинаковые математическое ожидание и дисперсию, равные
![]() .
.
Асимметрия и коэффициент эксцесса
распределения Пуассона равны соответственно 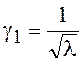 и
и 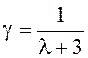 . С ростом
. С ростом ![]() распределение
Пуассона может быть аппроксимировано нормальным и при больших
распределение
Пуассона может быть аппроксимировано нормальным и при больших ![]() можно пользоваться приближенным выражением
можно пользоваться приближенным выражением
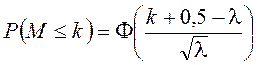 ,
,
где ![]() -
интеграл вероятности.
-
интеграл вероятности.
3.5.5. Распределения, связанные с равномерным
В начале главы была
рассмотрена СВ, все значения которой в интервале ![]() равновероятны.
ПВ такой величины
равновероятны.
ПВ такой величины ![]() имеет вид
имеет вид
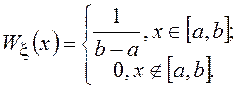 .
.
Характеристическая функция равномерного распределения равна
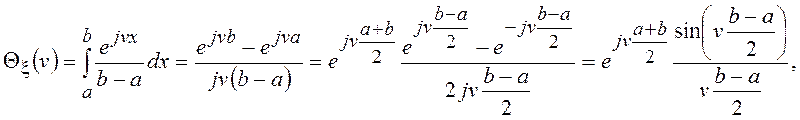
а для среднего значения и дисперсии справедливы соотношения
![]() =
=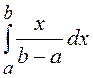 =
=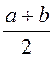 и
и ![]() =
=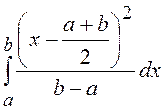 =
=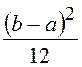 .
.
Асимметрия распределения
равна 0, коэффициент эксцесса ![]() .
.
С равномерным распределением приходится сталкиваться при изучении ошибок квантования (переход от непрерывного представления величины к дискретному, от аналогового сигнала к цифровому), при описании случайной начальной фазы гармонического колебания и во многих других случаях.
3.5.5.1. Рассмотрим задачу определения ПВ
случайной величины ![]() =
=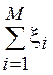 , где
, где ![]() - независимые СВ, каждая из которых
подчиняется равномерному распределению на промежутке
- независимые СВ, каждая из которых
подчиняется равномерному распределению на промежутке ![]() .
Эта задача может быть решена либо последовательным применением свертки, либо с
использованием ХФ. При большом числе слагаемых второй способ более
предпочтителен. При
.
Эта задача может быть решена либо последовательным применением свертки, либо с
использованием ХФ. При большом числе слагаемых второй способ более
предпочтителен. При ![]() =2, используя свертку двух
одинаковых равномерных распределений, будем иметь
=2, используя свертку двух
одинаковых равномерных распределений, будем иметь
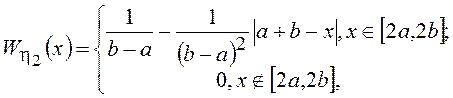
а ХФ
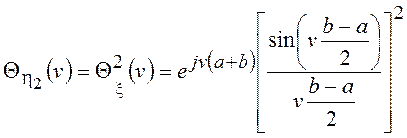 .
.
Полученное распределение по понятным причинам называется треугольным, или распределением Симпсона. Для определения среднего и дисперсии можно воспользоваться их свойствами, рассмотренными выше.
Так, математическое
ожидание будет равно сумме математических ожиданий слагаемых, т.е. ![]() =
=![]() +
+![]() =
=![]() . Дисперсия в силу независимости слагаемых
также равна сумме дисперсий слагаемых
. Дисперсия в силу независимости слагаемых
также равна сумме дисперсий слагаемых ![]() =
=![]() +
+![]() =
=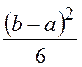 .
Асимметрия распределения равна нулю, а коэффициент эксцесса
.
Асимметрия распределения равна нулю, а коэффициент эксцесса ![]() . С ростом числа слагаемых
. С ростом числа слагаемых ![]() распределение суммы будет достаточно
быстро стремиться к нормальному закону
распределение суммы будет достаточно
быстро стремиться к нормальному закону
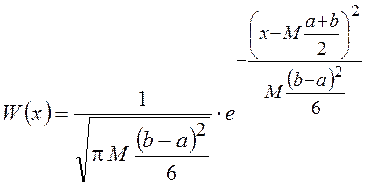 .
.

Рис. 15
Это часто используют при
моделировании нормальной СВ. Нужно, однако, помнить, что в отличие от
гауссовской, рассматриваемая СВ принимает значения в конечном интервале ![]() . На рис. 15 приведены графики равномерного
распределения (а) и ПВ суммы равномерно распределенных СВ при
. На рис. 15 приведены графики равномерного
распределения (а) и ПВ суммы равномерно распределенных СВ при ![]() =2, 3 (б, в) и
=2, 3 (б, в) и ![]() . Там же
пунктирной линией (для
. Там же
пунктирной линией (для ![]() =3) приведен график
аппроксимирующего нормального распределения (г).
=3) приведен график
аппроксимирующего нормального распределения (г).
3.5.5.2. Закон арксинуса.
Часто приходится
рассматривать СВ ![]() =
=![]() , где
, где ![]() - СВ, распределенная равномерно в
интервале
- СВ, распределенная равномерно в
интервале ![]() .
.
Пользуясь правилами функционального преобразования СВ, можно показать, что
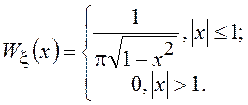
Функция распределения при этом будет равна
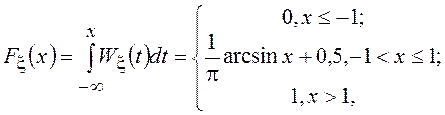
что и определяет название распределения.
Характеристическая функция для закона арксинуса
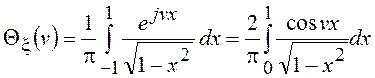 .
.
Выполняя замену
переменной ![]() , приходим к интегралу Парсеваля
, приходим к интегралу Парсеваля
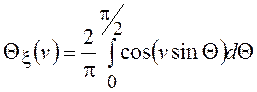 .
.
Следовательно, ![]() .
.
Математическое ожидание равно нулю, а для вычисления дисперсии удобно воспользоваться формулой
![]() =
=![]() =
=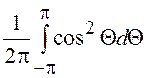 =
=![]() .
.
3.5.5.3. Распределение Коши.
Распределение Коши
встречается при решении следующей вероятностной задачи. Пусть из начала
координат проведен под случайным углом ![]() ,
равномерно распределенном в интервале
,
равномерно распределенном в интервале ![]() ,
отрезок, пересекающий прямую
,
отрезок, пересекающий прямую ![]() в случайной точке (
в случайной точке (![]() ,
,![]() ), рис. 17.
), рис. 17.
Требуется найти ПВ
случайной величины ![]() . Случайные величины
. Случайные величины ![]() и
и ![]() связаны
очевидным соотношением
связаны
очевидным соотношением 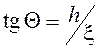 или
или 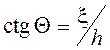 . Пользуясь правилами преобразования СВ и
учитывая, что
. Пользуясь правилами преобразования СВ и
учитывая, что 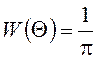 при
при ![]() =
=![]() , а
, а 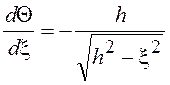 ,
получим окончательно
,
получим окончательно 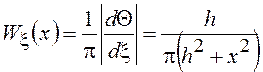 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.