Целевые установки развития и типы экономических моделей. Модели общего равновесия. Модели экономического взаимодействия. Связь между производственными функциями с взаимозаменяемыми ресурсами и функциями производственных затрат, страница 26

, где  – матрица коэффициентов удельных затрат, a R – вектор доступных запасов ресурсов.

Если при этом цену ресурсов обозначить за w, то вектор удельной добавленной стоимости можно представить следующим образом: . Посмотрим, какие изменения в нашей модели произойдут при введении данных ограничений:

Модель материально вещественных связей: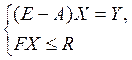

Модель межотраслевых зависимостей цен: .

Пусть теперь мы рассматриваем экономику, в которой две отрасли, которые производят соответственно два продукта и использует при этом два первичных ресурса – труд и капитал. Такую экономику можно описать следующей системой:

и  – как и прежде – трудоемкость и фондоёмкость

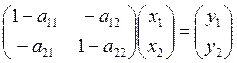
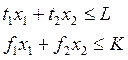
Для такой экономики можно сформулировать и доказать ряд теорем.

Теорема Рибчинского:

Увеличение доступного объёма одного из ресурсов при сохранении всех остальных параметров неизменными приводит к увеличению выпуска тех товаров, которые используют этот ресурс более интенсивно, и к уменьшению выпуска товаров, которые используют этот ресурс менее интенсивно.

Док-во:

Итак, пусть в экономике две отрасли. Причем первая отрасль капиталоёмкая, т.е.

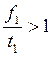
  , а вторая отрасль трудоёмкая:      .

Где  L и K доступное количество труда и капитала

Имеем следующие ресурсные ограничения:

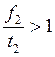
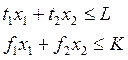
Так как нашей целевой установкой является максимизация выпуска, и чем больше затраты, тем больше выпуск, то в данной экономике будут использоваться все имеющиеся ресурсы, то есть представленные выше ограничения выполнятся как равенства:

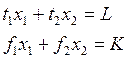
Из этой системы можно выразить  и :

               

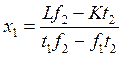
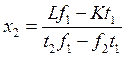
Пусть в экономике увеличилось доступное количество труда (допустим, в эту страну массово мигрировали китайцы или ещё что-то в этом духе), тогда изменение в выпуске обеих отраслей составит:

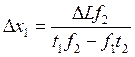 и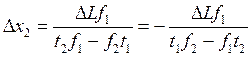

Так как вторая отрасль трудоемкая   ; а первая отрасль капиталоёмкая       , то

    – знаменатель обеих дробей отрицательный.

Что качается числителя, то доступное количество ресурса увеличилось, а фондоотдача не может быть отрицательной, то  и , значит

 – выпуск в капиталоёмкой отрасли уменьшился;

 – выпуск трудоёмкой отрасли увеличился.

Что и требовалось доказать.

Теорема Столпера-Самуэльсона

Повышение цены любого ресурса при неизменных остальных параметрах приводит к повышению цен тех ресурсов, которые используются относительно интенсивно в производстве данного продукта, и к снижению цен ресурсов, которые используются в производстве продукта менее интенсивно.

Док-во:

Теперь рассмотрим модель межотраслевой зависимости цен так же для  двухпродуктовой экономики, использующей два первичных ресурса.

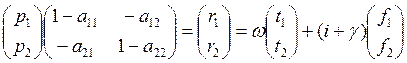
Кроме того, как и ранее, примем, что первая отрасль капиталоёмкая, вторая – трудоёмкая:

 и

Пусть , тогда имеем следующую систему уравнений:

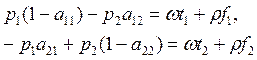
Выражаем цены ресурсов:

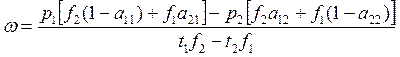
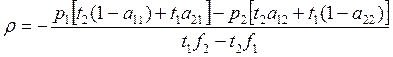
Пусть теперь увеличивается цена на продукцию первой отрасл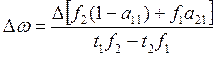и :

    и   .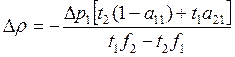

Как показано в доказательстве предыдущей теоремы: , кроме того,  и  из необходимых условий продуктивности матрицы A и экономического смысла трудоёмкости и фондоотдачи. Следовательно

 и

То есть с ростом цены на продукцию первой капиталоёмкой отрасли, цена капитала выросла, а цена труда упала.

Теорема доказана.

Хочется ещё раз отметить, что обе эти теоремы можно доказать только для двухпродуктовой экономики, использующей два ресурса.

Расширенная модель межотраслевого баланса

В рассматриваемой ранее версии межотраслевого баланса основной акцент делается на производственно-технических пропорциях экономики, при этом недостаточно внимания уделено взаимосвязям производства, занятости, потребления и доходов населения.

Теперь рассмотрим модель, в которой в составе продукции, направляемой на конечное использование () выделяют две части:

·  расходы населения (фонд потребления);

·  прочие расходы (расходы государства, инвестиции ит.д.).

Расходы населения на конечное потребление  зависят от получаемого дохода R, который в свою очередь складывается из трудового дохода (получаемой заработной платы) и прочих доходов, несвязанных с производственной деятельностью.