в) Однако, такая запись допускает, что все частные критерии одинаково важны. Если захотеть ввести различную степень важности, то можно использовать следующую функцию:
F(X) = 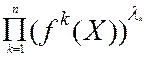
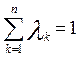
Условная субоптимизация
Однако рассмотрим теперь субоптимизации. Причем ненулевое λ стоит перед функцией полезности потребителей. То есть задача имеет вид:
U(X2) → max
g1(X1) – X2![]() Q
Q
g2(X1) ![]() R
R
X1, X2 ![]() 0
0
Кроме того,
если рассматривать открытую экономику, то первое ограничение можно переписать,
учитывая S – сальдо
внешнеторговых балансов g1(X1)
– X2![]() Q
+ S
Q
+ S
При этом предполагается,
что![]() – все остальные
целевые функции не ниже допустимого уровня.
– все остальные
целевые функции не ниже допустимого уровня.
Лирическое отступление лектора:
А какие бывают цели по отношению друг к другу? Цели бывают:
· взаимодействующие
· нейтральные
· конфликтные
Теперь к делу.
Сопоставим
ограничениям модели множители Лагранжа. Обозначим векторы строки для неравенств
g1(X1) – Q ![]() X2 – как V = (vs1), а для неравенств g2(X1)
X2 – как V = (vs1), а для неравенств g2(X1) ![]() R – как W = (ws2).
Составим Лагранжиан:
R – как W = (ws2).
Составим Лагранжиан:
L(X, V, W) = U(X2) – V(X2 + Q – g1(X1)) + W(R– g2(X1))
Из теории нелинейного программирования известно :))
V = (vs1) = 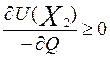 W =
(ws2) =
W =
(ws2) = 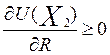
Множитель Лагранжа даёт информацию, насколько чувствительно изменение целевой функции от изменения правой части соответствующего ограничения. Данные величины имеют разные названия – двойственные переменные, оценки оптимального плана, объективно обусловленные оценки, теневые цены, цены оптимального плана. Я бы хотела заострить внимание на том, что это – цены.
Обоснование этого факта для любителей:
Имеем задачу:
f(X) → max при ограничениях
g(X) ![]() b где g(X) = [gs(X)],
s
b где g(X) = [gs(X)],
s![]() M и
b – вектор из вещественных чисел
M и
b – вектор из вещественных чисел
X ![]() 0
0
Задача нелинейного программирования обычно решается с помощью функции Лагранжа
L(X, Y) = f(X) + Y(b – g(X))
Данный
Лагранжиан рассматривается на множестве векторов X![]() 0, Y
0, Y![]() 0. Компоненты m-мерного
вектора-строки Y = (ys),
как водится, называются множителями Лагранжа.
0. Компоненты m-мерного
вектора-строки Y = (ys),
как водится, называются множителями Лагранжа.
Найдём векторы частных производных первого порядка данного Лагранжиана.
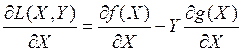
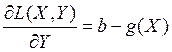
Теперь надо вспомнить второй семестр, Матан, поиск условного экстремума. Тогда задача имела вид
f(X) → max т.е. ограничения в виде равенств и нет условий неотрицательности
g(X) = b переменных
Это так называемая задача в классической форме. Для таких задач мы тоже строили функцию Лагранжа и необходимым условием максимума f(X) являлось равенство нулю всех частных производных этой функции Лагранжа нулю.
Однако в нашей модели присутствие неравенств и условий неотрицательности имеет принципиальное значение. Поэтому попытаемся свести имеющуюся у нас задачу к задаче в классической форме.
Если вспомнить условия дополняющей нежесткости, то получим, что в оптимальной точке (X*, Y*), должны выполняться следующие условия
1. 
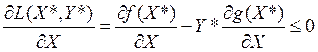
2. 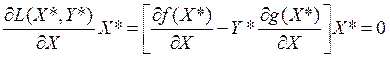
3. X*![]() 0
0
4. 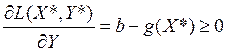
5. 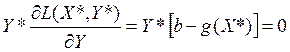
6. Y*![]() 0
0
Для анализа решений оптимизационных задач важное значение имеет вопрос: какое влияние оказывает изменение параметров правой части – вектора b на значение целевой функции f(X)?
В отношении тех ограничений, которые в оптимальном плане выполняются как строгие неравенства gs(X*) < bs, ответ вполне очевиден: малые изменения bs не изменяют равенства f(X)=f(X*). Если ограничение выполняется как строгое неравенство, значит, этот ресурс недефицитен. Тогда некоторое изменение доступного его количества не изменит выбор оптимального X*.
Предположим,
что известно, какие ограничения выполняются как равенства, а какие как
неравенства, а также известно какие именно переменные в оптимальном плане равны
нулю, а какие положительны. Пронумеруем ограничения и переменные следующим
образом: первые m1 ограничений выполняются
как равенства, 0![]() m1
m1![]() m, а остальные (m- m1) ограничений как
строгие неравенства; первые n1 переменных
положительны 0
m, а остальные (m- m1) ограничений как
строгие неравенства; первые n1 переменных
положительны 0![]() n1
n1![]() n, а остальные (n- n1) переменных равны
нулю. Тогда
n, а остальные (n- n1) переменных равны
нулю. Тогда
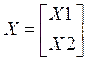 ; Y = (Y1, Y2);
; Y = (Y1, Y2);
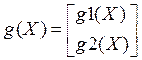 ;
; 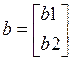
Неравенства и нулевые переменные можно исключить из задачи (предполагается, что нулевые переменные останутся нулевыми при некоторых изменениях исходных данных). В результате получаем классическую задачу:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.