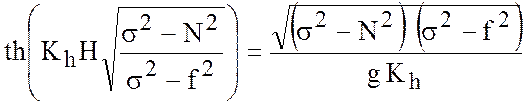 . (5.30)
. (5.30)
Это и есть общее дисперсионное соотношение, которое может быть упрощено при определенных допущениях
- если ![]() (короткие
волны)
(короткие
волны) ![]() (
(![]() , т.е.
пренебрегаем стратификацией и вращением);
, т.е.
пренебрегаем стратификацией и вращением);
- если ![]() (длинные
волны)
(длинные
волны) 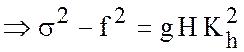 .
.
Пересечение решений типа б) ![]() -задачи с кривыми 1-го типа
-задачи с кривыми 1-го типа ![]() -задачи называются внутренними
гравитационными волнами. Они могут возникать только, если
-задачи называются внутренними
гравитационными волнами. Они могут возникать только, если ![]() , то есть
, то есть ![]() . С
большой точностью существование этого типа волн не зависит от свободной
поверхности, то есть условие
. С
большой точностью существование этого типа волн не зависит от свободной
поверхности, то есть условие ![]() слабо исказит решение. Например,
двухслойная жидкость, где поверхность раздела между слоями жидкости разной
плотности испытывает колебания, будучи зажатой между двумя пластинами.
слабо исказит решение. Например,
двухслойная жидкость, где поверхность раздела между слоями жидкости разной
плотности испытывает колебания, будучи зажатой между двумя пластинами.
Исключив константу разделения ![]() из (5.29) и (5.27), получим дисперсионное
соотношение для внутренних гравитационных волн
из (5.29) и (5.27), получим дисперсионное
соотношение для внутренних гравитационных волн
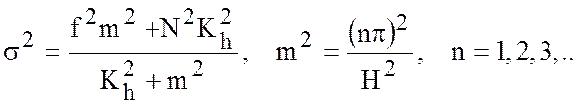
где ![]() - некоторый аналог волнового
числа по вертикали.
- некоторый аналог волнового
числа по вертикали.
Рассмотрим предельный случай. Если
![]() , то есть жидкость однородна, то имеем
обязательное пересечение собственных кривых
, то есть жидкость однородна, то имеем
обязательное пересечение собственных кривых ![]()
![]() -задачи с собственными кривыми 2-го типа
-задачи с собственными кривыми 2-го типа ![]() -задачи.
-задачи.
Если ![]() , то это
возможно при
, то это
возможно при ![]() . Тогда пересечение кривых второго типа
. Тогда пересечение кривых второго типа ![]() -задачи и
-задачи и ![]()
![]() -задачи соответствует гироскопическим
(инерциальным) волнам, возникающим за счет вращения Земли. Дисперсионное
соотношение для гироскопических волн получим, исключая
-задачи соответствует гироскопическим
(инерциальным) волнам, возникающим за счет вращения Земли. Дисперсионное
соотношение для гироскопических волн получим, исключая ![]() из
(5.29) и (5.28) при
из
(5.29) и (5.28) при ![]() :
:
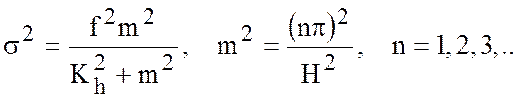
Отметим, что всегда ![]() . При
. При ![]() -
необходимое условие существования инерциальных волн.
-
необходимое условие существования инерциальных волн.
5.3. Волны Россби.
Мы рассматривали колебания на ![]() -плоскости. Рассмотрим
-плоскости. Рассмотрим ![]() -плоскость (
-плоскость (![]() ) и
выясним существование решений
) и
выясним существование решений ![]() -задачи, пересекающих
-задачи, пересекающих ![]() . При
. При ![]() таких
решений нет. Однако на
таких
решений нет. Однако на ![]() -плоскости это возможно. В
третьем уравнении
-плоскости это возможно. В
третьем уравнении ![]() -задачи положим
-задачи положим ![]() , тогда
, тогда ![]() . Последнее условие позволяет ввести
функцию тока:
. Последнее условие позволяет ввести
функцию тока: ![]() ,
, ![]() . Из
первых двух уравнений движения исключаем
. Из
первых двух уравнений движения исключаем ![]() .
.
![]() . (5.31)
. (5.31)
Представим ![]() , тогда
, тогда ![]() ,
отсюда дисперсионное соотношение для этого типа волн, называемых волнами
Россби, имеет вид
,
отсюда дисперсионное соотношение для этого типа волн, называемых волнами
Россби, имеет вид
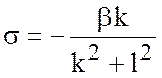 . (5.32)
. (5.32)
В одномерном случае ![]() , т.е. чем больше волновое число, тем меньше
фазовая скорость. Знак минус в дисперсионном соотношении (5.32) означает, что
фазовая скорость отрицательна, то есть волны Россби распространяются с востока
на запад.
, т.е. чем больше волновое число, тем меньше
фазовая скорость. Знак минус в дисперсионном соотношении (5.32) означает, что
фазовая скорость отрицательна, то есть волны Россби распространяются с востока
на запад.
Заметим, что волны Россби можно получить, рассматривая закон сохранения абсолютного вихря. В нашем случае относительный вихрь имеет вид:
![]() ,
,
таким образом из соотношения (5.31), переходя от гармоник к производным по времени, получим
![]()
или
![]() .
.
Но
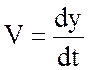 ,
,
то есть
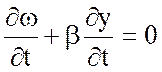 ,
,
или
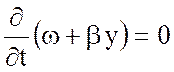 . (5.33)
. (5.33)
В последнем соотношении можем заменить ![]() на
на ![]() , так
как
, так
как ![]() . Тогда имеем закон сохранения абсолютного
вихря
. Тогда имеем закон сохранения абсолютного
вихря
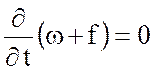 , (5.34)
, (5.34)
или, в общем случае, вводя конвективные производные в уравнения движения, можно получить закон сохранения абсолютного вихря вдоль траектории
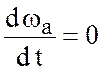 . (5.35)
. (5.35)
Таким образом, при перемещении
точки на юг, ![]() - планетарный вихрь уменьшается,
тогда из закона сохранения абсолютного вихря следует увеличение относительного
вихря (см. Рис.5.4). Возникает завихренность, возвращающая частицу к исходному
положению. Проходя ее из-за сил инерции частица следует на север, увеличивая
планетарный вихрь. Для сохранения абсолютного вихря частица приобретает меньшее
значение относительного вихря, что закручивает ее в обратном направлении. Таким
образом, частица колеблется возле положения равновесия. Закон сохранения абсолютного
вихря объясняет механизм формирования планетарных волн Россби, имеющих фазовую
скорость, направленную на запад.
- планетарный вихрь уменьшается,
тогда из закона сохранения абсолютного вихря следует увеличение относительного
вихря (см. Рис.5.4). Возникает завихренность, возвращающая частицу к исходному
положению. Проходя ее из-за сил инерции частица следует на север, увеличивая
планетарный вихрь. Для сохранения абсолютного вихря частица приобретает меньшее
значение относительного вихря, что закручивает ее в обратном направлении. Таким
образом, частица колеблется возле положения равновесия. Закон сохранения абсолютного
вихря объясняет механизм формирования планетарных волн Россби, имеющих фазовую
скорость, направленную на запад.
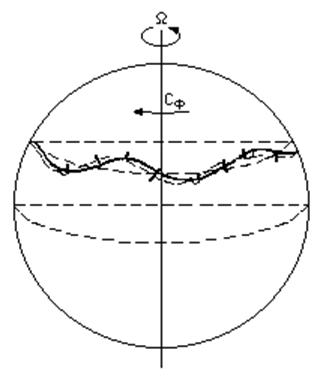
Рис. 5.4. Схематическое представление механизма формирования волн Россби.
5.4. Общая схема классификации свободных волн в океане
Окончательная схематичная картина пересечения собственных кривых V и H представлена на Рис.5.5. Цифрами отмечены все типы свободных волны, полученные в анализе разделов 5.1. - 5.3.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.