Анализ волновых движений в океане. Уравнения геофизической гидродинамики с учетом турбулентности. Пограничные слои в океане, страница 14

Плотность на верхней границе геострофической области должна согласовываться с заданным полем плотности на поверхности, которое практически не меняется в тонком экмановском слое у поверхности океана. Это условие может быть записано в размерной форме как

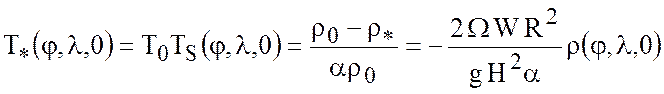              (7.61)

или

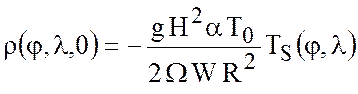,                              (7.62)

где  - характерная величина изменений заданной поверхностной температуры и  - коэффициент термического расширения. Безразмерная функция  имеет порядок  и описывает горизонтальную структуру поля поверхностной температуры. Для того чтобы  могло быть переменной порядка , как это предполагалось при выводе (7.48), (7.49),  выберем вертикальный масштаб движения  равным

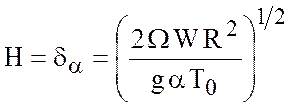.                                        (7.63)

Вертикальный масштаб  называется «адвективным» масштабом. При таком выборе вертикального масштаба горизонтальные изменения плотности, создаваемые ветровой циркуляцией, имеют одинаковый порядок величины с горизонтальными изменениями плотности, заданной на верхней границе. Если , , ,  и  (экмановская вертикальная скорость) равна , то . Эта оценка обнадеживает, поскольку величина  находится в неплохом соответствии с наблюдаемой глубиной термоклина, которая изменяется от 1000 м в средних широтах до 200 м в тропической и полярной зонах. Так как глубина  значительно меньше глубины океана, представляется разумным рассматривать термоклин как пограничный слой; в соответствии с этим при постановке граничных условий на нижней границе  можно считать, что температура на глубинах, больших , асимптотически стремится к некоторому горизонтально однородному распределению. Так как  много меньше глубины океана, то  будет меняться от больших отрицательных величин до нуля. Таким образом, при  аномалия плотности должна затухать, а  должна стремиться к асимптотическому значению.

В принципе граничные условия для (7.55) должны задаваться также и на боковых границах, чтобы обеспечить единственность решения этого дифференциального уравнения в частных производных. Такие условия не являются физическими условиями, заданными на границе океанского бассейна, поскольку эти границы отделены от геострофической области узкими зонами пограничных течений, в которых существенна адвекция и диффузия тепла и вихря. Поэтому для постановки граничных условий для уравнений, описывающих динамику во внутренней геострофической области, необходимо сначала провести анализ погранслойных решений, выразив их через неизвестное пока решение во внутренней области; после этого искомые граничные условия могут быть получены путем согласования решений во внутренней области и в пограничных слоях. Эта процедура в настоящем случае нелинейной динамики стратифицированной жидкости слишком сложна для того, чтобы ее можно было в действительности провести. Пока при анализе проблемы термоклина удалось построить лишь семейство решений системы (7.54), (7.55), удовлетворяющих только граничным условиям по вертикали. Это является слабым местом существующих теорий термоклина, поскольку остается непонятным, какое из имеющихся решений (если таковое найдется) будет удовлетворять физически правильным условиям на боковых границах.

В настоящее время имеется несколько частных решений уравнений теории термоклина, неплохо описывающих наблюдаемые особенности полей плотности и температуры. Однако,  ни одно из этих решений не свободно от серьезных недостатков, так что полностью удовлетворительного решения поставленной проблемы термоклина пока не имеется.

Нидлер (1967) предложил частное решение вида

,                                        (7.64)

где слагаемое  представляет баротропное поле. Бароклинная компонента поля давления экспоненциально затухает вниз со скоростью затухания, равной величине , которая должна быть положительной. Скорость затухания  предполагается априори функцией долготы и широты. Таким образом, в этом частном решении профили плотности на всех вертикалях подобны; отличие этих профилей обусловлено лишь горизонтальными изменениями растягивающего множителя . Подставляя (7.64) в (7.54), получаем