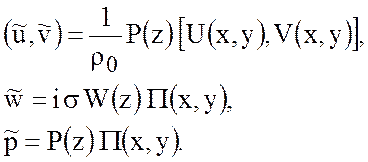 (5.13)
(5.13)
Подставим (5.13) в последнее уравнение (5.12) и получим
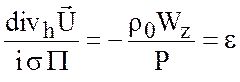 , (5.14)
, (5.14)
где ![]() , а
, а ![]() - константа разделения. Тогда систему
уравнений (5.12) можно записать в виде двух систем, где одна зависит только от вертикальной
координаты, а другая - от горизонтальных координат.
- константа разделения. Тогда систему
уравнений (5.12) можно записать в виде двух систем, где одна зависит только от вертикальной
координаты, а другая - от горизонтальных координат.
Для функций ![]() ,
, ![]() ,
, ![]() ставится
ставится
![]() -задача (Horyzontal)
-задача (Horyzontal)
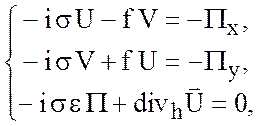 (5.15)
(5.15)
а для функций ![]() и
и ![]() -
- ![]() -задача
(Vertical)
-задача
(Vertical)
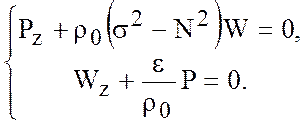 (5.16)
(5.16)
Для ![]() -задачи
граничных условий нет, так как океан безграничен, а для
-задачи
граничных условий нет, так как океан безграничен, а для ![]() -задачи
-задачи
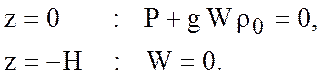 (5.17)
(5.17)
Чтобы решить поставленную
задачу, нужно найти все возможные ![]() и
и ![]() , для которых задачи (5.15) и (5.16), при
условиях (5.17), имеют решение. Пересечения собственных кривых
, для которых задачи (5.15) и (5.16), при
условиях (5.17), имеют решение. Пересечения собственных кривых ![]()
![]() -задач, образованные на
этой плоскости будут решениями общей задачи и дают частоты возможных свободных
колебаний в океане. Заметим, что
-задач, образованные на
этой плоскости будут решениями общей задачи и дают частоты возможных свободных
колебаний в океане. Заметим, что ![]() -задача не зависит от
вращения системы координат, потому что в ней отсутствует параметр Кориолиса
-задача не зависит от
вращения системы координат, потому что в ней отсутствует параметр Кориолиса ![]() , а для
, а для ![]() -задачи
неважно каким образом стратифицирована система (в уравнениях отсутствует
-задачи
неважно каким образом стратифицирована система (в уравнениях отсутствует ![]() ).
).
5.2. Анализ простейших случаев.
Пусть ![]() .
Система (5.16) может быть сведена к одному уравнению относительно
.
Система (5.16) может быть сведена к одному уравнению относительно ![]()
![]() . (5.18)
. (5.18)
Рассмотрим графическое решение этой задачи
1. ![]()
а) ![]() ;
;
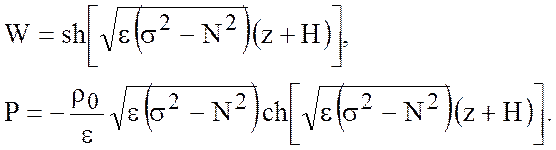
При ![]() ,
тогда собственные значения можно найти из уравнения
,
тогда собственные значения можно найти из уравнения
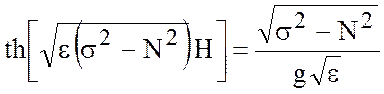 ; (5.19)
; (5.19)
б) ![]() ;
;
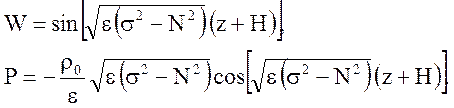
Тогда уравнение для собственных значений примет вид
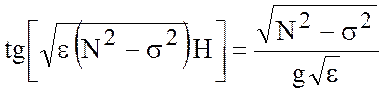 ; (5.20)
; (5.20)
2. ![]()
в) ![]() ;
;
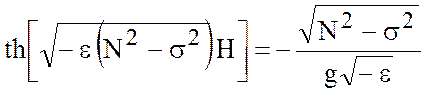 ; (5.21)
; (5.21)
г) ![]() ;
;
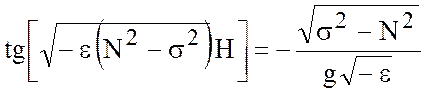 . (5.22)
. (5.22)
При графическом анализе получаем:
a) Рис. 5.1.а - один корень (баротропные волны),
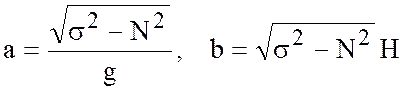 , (5.23)
, (5.23)
б) Рис.5.1.б - бесконечное число корней,
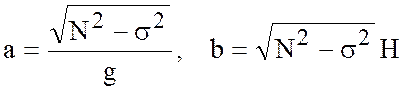 , (5.24)
, (5.24)
в) Рис.5.1.в - корней нет,
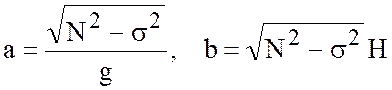 , (5.25)
, (5.25)
г) Рис.5.1.г - бесконечное число корней (нет ![]() ),
),
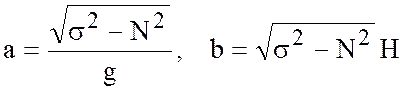 . (5.26)
. (5.26)
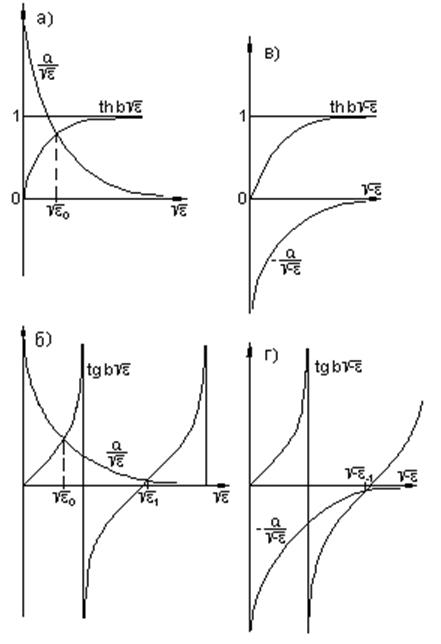
Рис. 5.1.
Можно рассмотреть следующие асимптотики решений:
1) ![]() .
.
а) При ![]() выполняется
выполняется ![]() (с определенной
точностью);
(с определенной
точностью);
б) Когда ![]() и
и ![]() мало,
т.е. стратификация слабая,
мало,
т.е. стратификация слабая, 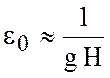 , а
, а ![]() приближаются к оси
приближаются к оси ![]() ,
следовательно, пренебрегая малыми правыми частями, для них получим уравнение
,
следовательно, пренебрегая малыми правыми частями, для них получим уравнение
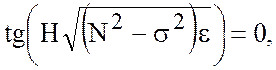 (5.27)
(5.27)
то есть
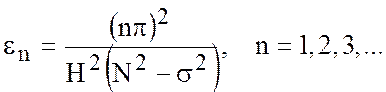
2) ![]() .
.
в) нет корней;
г) аналогично предыдущему (вариант б) получаем тригонометрическое уравнение :
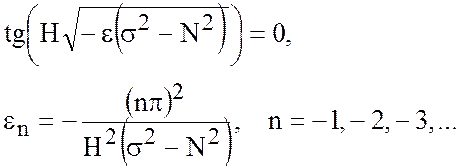 (5.28)
(5.28)
Таким образом полная картина для ![]() -задачи имеет вид:
-задачи имеет вид:
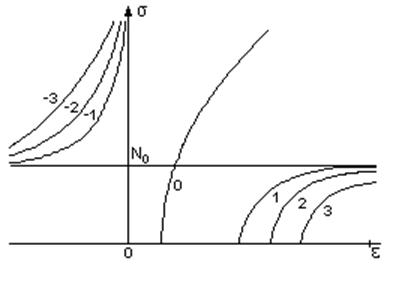
Рис. 5.2. Собственные кривые ![]() -задачи. Картина симметрична относительно
оси
-задачи. Картина симметрична относительно
оси ![]() .
.
Переходим к рассмотрению ![]() -задачи.
-задачи.
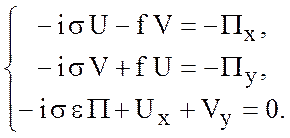
Так как океан безграничный, то ищем решение в виде
![]() ,
,
где ![]() -
волновые числа по
-
волновые числа по ![]() соответственно. Тогда имеем
соответственно. Тогда имеем
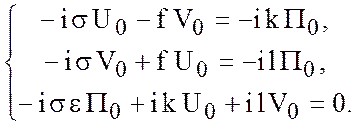
Это однородная система. Для ее однозначной разрешимости мы должны потребовать, чтобы дискриминант равнялся нулю, т.е.
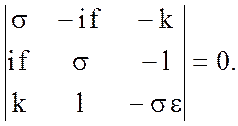
Отсюда,
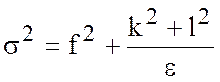 . (5.29)
. (5.29)
Выражение (5.29) дает
соотношение для собственных кривых ![]() -задачи (схематично
представленное на рис. 5.3). График кривых симметричен относительно
-задачи (схематично
представленное на рис. 5.3). График кривых симметричен относительно ![]() .
.
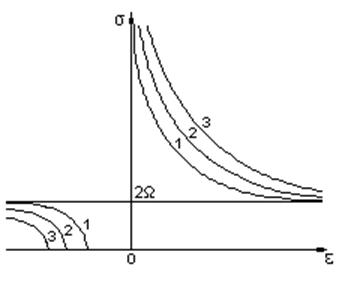
Рис. 5.3. Цифры у кривых соответствуют
различным значениям среднего волнового числа 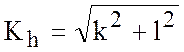 .
.
Асимптотикой для ![]() -задачи
является
-задачи
является ![]() , а для
, а для ![]() -задачи
-
-задачи
- ![]() , поэтому пересечение собственных кривых
, поэтому пересечение собственных кривых ![]()
![]() -задачи и собственных кривых
первого типа
-задачи и собственных кривых
первого типа ![]() -задачи происходит при
-задачи происходит при ![]() , что соответствует поверхностным
гравитационным волнам, которые полностью определяются эффектом свободной
поверхности. Этот тип волн возникает за счет существования свободной границы и
условий на ней. Примером таких волн является цунами, которая представляет собой
очень длинную гравитационную волну. Если на границе положить
, что соответствует поверхностным
гравитационным волнам, которые полностью определяются эффектом свободной
поверхности. Этот тип волн возникает за счет существования свободной границы и
условий на ней. Примером таких волн является цунами, которая представляет собой
очень длинную гравитационную волну. Если на границе положить ![]() , то поверхностные волны исчезают, в
соответствии с условием твердой крышки.
, то поверхностные волны исчезают, в
соответствии с условием твердой крышки.
Чтобы получить общее
дисперсионное соотношение, исключим ![]() из (5.29) и выражения (5.19).
В результате получим
из (5.29) и выражения (5.19).
В результате получим
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.